在Mathematica中, 内置了函数RegionProduct。这个函数能用来绘制康托尔集合。这个函数的基本意思是指
RegionProduct[reg1,reg2,…]
表示区域reg1, reg2, ….的笛卡尔积使用这个函数,我们编写三个函数:
ClearAll[cantorrule, cantorRegion, cantorDust]
(*康托尔集的生成法则*)
cantorrule[s_: 1/3] := ReplaceAll[{a_, b_} :> {{a, a + (b - a) (1 - s)/2}, {a + (b - a) (1 + s)/2, b}}];
(*生成一维的用来做乘积的区域*)
cantorRegion[s_: 1/3][t_Integer?NonNegative] := MeshRegion[ List /@ Flatten[Nest[Apply[Join]@*Map[cantorrule[s]], {{0, 1}}, t]], Line @ Partition[Range[2^(t + 1)], 2]]
(*显示成像区域*)
cantorDust[s_: 1/3][t_Integer?NonNegative, dim_: 1] := RegionProduct @@ Table[cantorRegion[s][t], dim]Labeled[Grid[Transpose @ {Show[cantorDust[][#, 1], ImageSize -> Medium] & /@ Range[3], Show[cantorDust[][#, 2], ImageSize -> Medium] & /@ Range[3], Show[cantorDust[][#, 3], ImageSize -> Medium] & /@ Range[3]}, Dividers -> All], Style["s = 1/3", 36], Top]
也可以改变s的值为1/4和5/12等,来试一下显示效果。
Labeled[Grid[{Prepend[Style["s", 24]][Style["t = " <> ToString@#, 16] & /@ {1, 2, 3}], Prepend[Style["1/4", 16]][ Show[cantorDust[1/4][#, 1], ImageSize -> Medium] & /@ Range[3]], Prepend[Style["1/3", 16]][ Show[cantorDust[1/3][#, 1], ImageSize -> Medium] & /@ Range[3]], Prepend[Style["5/12", 16]][ Show[cantorDust[5/12][#, 1], ImageSize -> Medium] & /@ Range[3]]}, Dividers -> All], Style["dim=1", 36], Top]
Labeled[Grid[{Prepend[Style["s", 24]][ Style["t = " <> ToString@#, 16] & /@ {1, 2, 3}], Prepend[Style["1/4", 16]][ Show[cantorDust[1/4][#, 2], ImageSize -> Medium] & /@ Range[3]], Prepend[Style["1/3", 16]][ Show[cantorDust[1/3][#, 2], ImageSize -> Medium] & /@ Range[3]], Prepend[Style["5/12", 16]][ Show[cantorDust[5/12][#, 2], ImageSize -> Medium] & /@ Range[3]]}, Dividers -> All], Style["dim=2", 36], Top] Export[ FileNameJoin[ {NotebookDirectory[], "cantor_dust_2d_collection.png"} ], % ]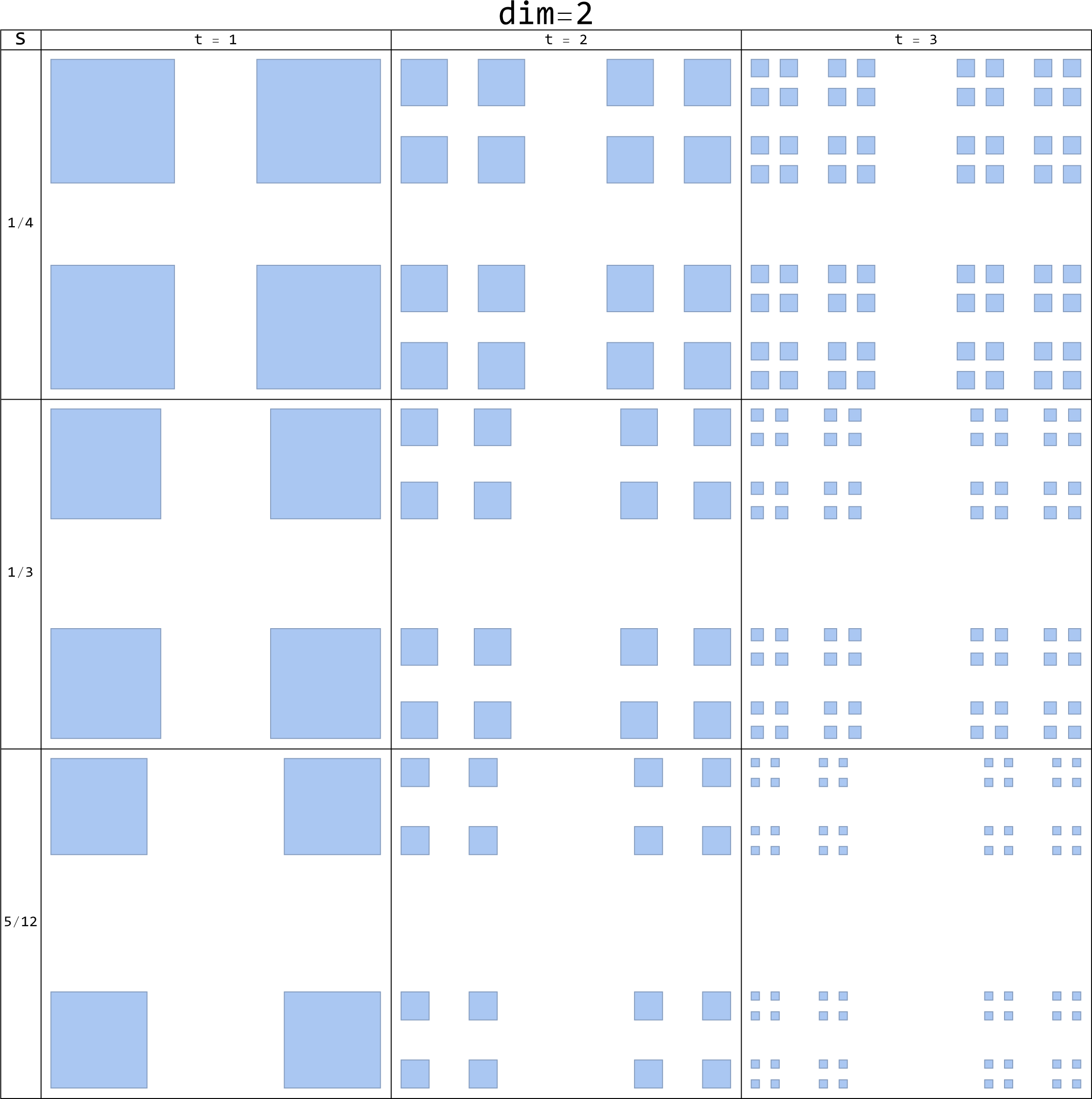




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








