python学习笔记（自用）第八天

最新推荐文章于 2025-05-04 19:41:26 发布

明天见ˇ

最新推荐文章于 2025-05-04 19:41:26 发布

阅读量1.1k

点赞数 33

文章标签： python 学习笔记

本文链接：https://blog.csdn.net/weixin_67939414/article/details/147590383

版权

函数（VI）- 装饰器

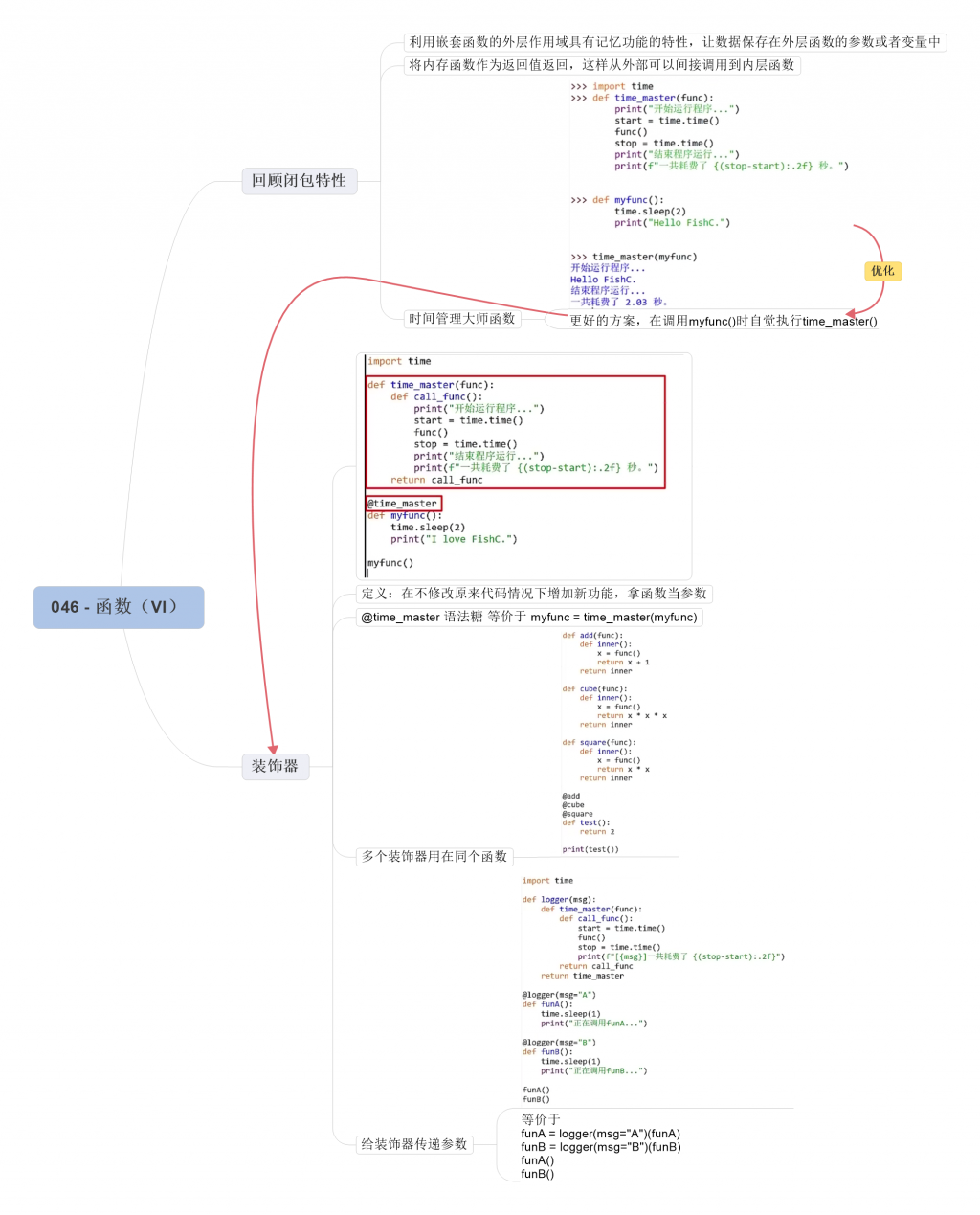
1. 装饰器

装饰器本质上也是一个函数，它可以让其他函数在不需要做任何代码变动的前提下增加额外的功能。

请看下面代码：

import time
   
def time_master(func):
    def call_func():
        print("开始运行程序...")
        start = time.time()
        func()
        stop = time.time()
        print("结束程序运行...")
        print(f"一共耗费了 {(stop-start):.2f} 秒。")
    return call_func
   
@time_master
def myfunc():
    time.sleep(2)
    print("I love FishC.")
   
myfunc()

程序实现如下：

开始运行程序...
I love FishC.
结束程序运行...
一共耗费了 2.01 秒

使用了装饰器，我们并不需要修改原来的代码，只需要在函数的上方加上一个 @time_master，然后函数就能够实现统计运行时间的功能了。

这个 @ 加上装饰器名字其实是个语法糖，装饰器原本的样子应该这么调用的：

我们在 f-string 里面谈到过语法糖，我们说语法糖是某种特殊的语法，对语言的功能没有影响，但对程序员来说，有更好的易用性，简洁性、可读性和方便性。

import time
   
def time_master(func):
    def call_func():
        print("开始运行程序...")
        start = time.time()
        func()
        stop = time.time()
        print("结束程序运行...")
        print(f"一共耗费了 {(stop-start):.2f} 秒。")
    return call_func
   
def myfunc():
    time.sleep(2)
    print("I love FishC.")
   
myfunc = time_master(myfunc)
myfunc()

这个就是装饰器的实现原理啦~

多个装饰器也可以用在同一个函数上：

def add(func):
    def inner():
        x = func()
        return x + 1
    return inner
   
def cube(func):
    def inner():
        x = func()
        return x * x * x
    return inner
   
def square(func):
    def inner():
        x = func()
        return x * x
    return inner
   
@add
@cube
@square
def test():
    return 2
   
print(test())

程序实现如下：

这样的话，就是先计算平方（square 装饰器），再计算立方（cube 装饰器），最后再加 1（add 装饰器）。

如何给装饰器传递参数呢？

答案是添加多一层嵌套函数来传递参数：

import time
   
def logger(msg):
    def time_master(func):
        def call_func():
            start = time.time()
            func()
            stop = time.time()
            print(f"[{msg}]一共耗费了 {(stop-start):.2f}")
        return call_func
    return time_master
   
@logger(msg="A")
def funA():
    time.sleep(1)
    print("正在调用funA...")
   
@logger(msg="B")
def funB():
    time.sleep(1)
    print("正在调用funB...")
   
funA()
funB()

程序实现如下：

正在调用funA...
[A]一共耗费了 1.01
正在调用funB...
[B]一共耗费了 1.04

我们将语法糖去掉，拆解成原来的样子，你就知道原理了：

import time
   
def logger(msg):
    def time_master(func):
        def call_func():
            start = time.time()
            func()
            stop = time.time()
            print(f"[{msg}]一共耗费了 {(stop-start):.2f}")
        return call_func
    return time_master
   
def funA():
    time.sleep(1)
    print("正在调用funA...")
   
def funB():
    time.sleep(1)
    print("正在调用funB...")
   
funA = logger(msg="A")(funA)
funB = logger(msg="B")(funB)
   
funA()
funB()

程序实现如下：

正在调用funA...
[A]一共耗费了 1.02
正在调用funB...
[B]一共耗费了 1.01

这里其实就是给它裹多一层嵌套函数上去，然后通过最外层的这个函数来传递装饰器的参数。

这样，logger(msg="A") 得到的是 timemaster() 函数的引用，然后再调用一次，并传入 funA，也就是这个 logger(msg="A")(funA)，得到的就是 call_func() 函数的引用，最后将它赋值回 funA()。

咱们对比一下没有参数的描述器，这里其实就是添加了一次调用，然后通过这次调用将参数给传递进去而已。

2. 本节思维导图

函数（VII）- lambda表达式

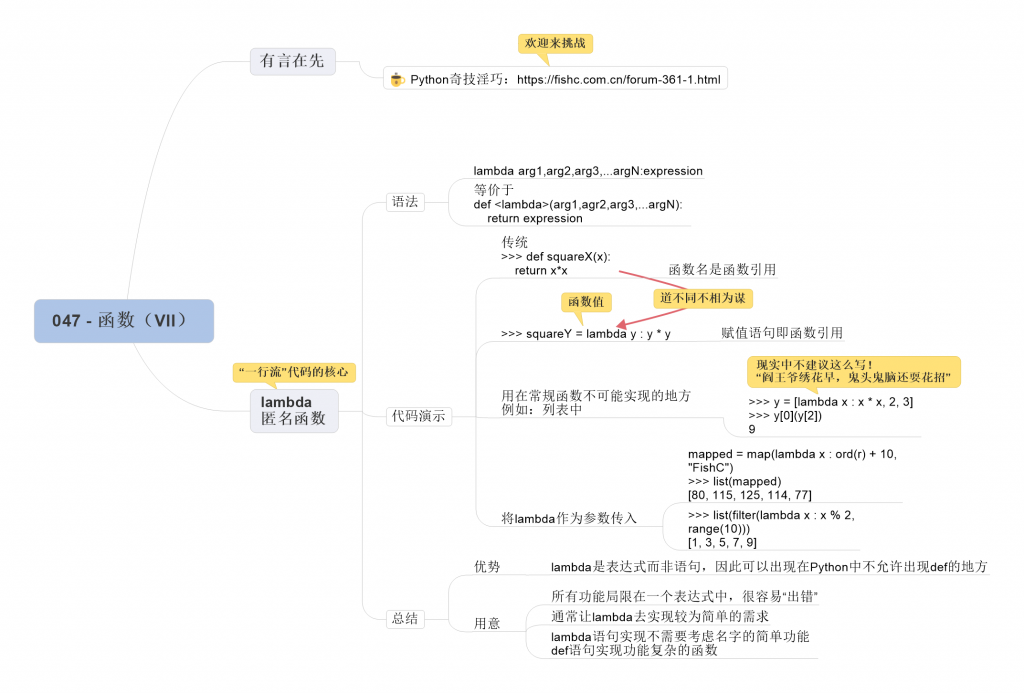
1. lambda 表达式

lambda 表达式，也就是大牛们津津乐道的匿名函数。

只要掌握了 lambda 表达式，你也就掌握了一行流代码的核心 —— 仅使用一行代码，就能解决一件看起来相当复杂的事情。

它的语法是这样的：

lambda arg1, arg2, arg3, ... argN : expression

lambda 是个关键字，然后是冒号，冒号左边是传入函数的参数，冒号后边是函数实现表达式以及返回值。

我们可以将 lambda 表达式的语法理解为一个极致精简之后的函数，如果使用传统的函数定义方式，应该是这样：

def <lambda>(arg1, arg2, arg3, ... argN):
... return expression

如果要求我们编写一个函数，让它求出传入参数的平方值，以前我们这么写：

>>> def squareX(x):
... return x * x
...
>>> squareX(3)
9

现在我们这么写：

>>> squareY = lambda y : y * y
>>> squareY(3)
9

传统定义的函数，函数名就是一个函数的引用：

>>> squareX
<function squareX at 0x0000015E06668F70>

而 lambda 表达式，整个表达式就是一个函数的引用：

>>> squareY
<function <lambda> at 0x0000015E06749EE0>

2. lambda 表达式的优势

lambda 是一个表达式，因此它可以用在常规函数不可能存在的地方：

>>> y = [lambda x : x * x, 2, 3]
>>> y[0](y[1])
4
>>> y[0](y[2])
9

注意：这里说的是将整个函数的定义过程都放到列表中哦~

3. 与 map() 和 filter() 函数搭配使用

利用 lambda 表达式与 map() 和 filter() 函数搭配使用，会使代码显得更加 Pythonic：

>>> list(mapped = map(lambda x : ord(x) + 10, "FishC"))
[80, 115, 125, 114, 77]
>>> list(filter(lambda x : x % 2, range(10)))
[1, 3, 5, 7, 9]

4. 总结

lambda 是一个表达式，而非语句，所以它能够出现在 Python 语法不允许 def 语句出现的地方，这是它的最大优势。

但由于所有的功能代码都局限在一个表达式中实现，因此，lambda 通常只能实现那些较为简单的需求。

当然，Python 肯定是有意这么设计的，让 lambda 去做那些简单的事情，我们就不用花心思去考虑这个函数叫什么，那个函数叫什么……

def 语句则负责用于定义功能复杂的函数，去处理那些复杂的工作。

5. 本节思维导图

函数（VIII）- 生成器

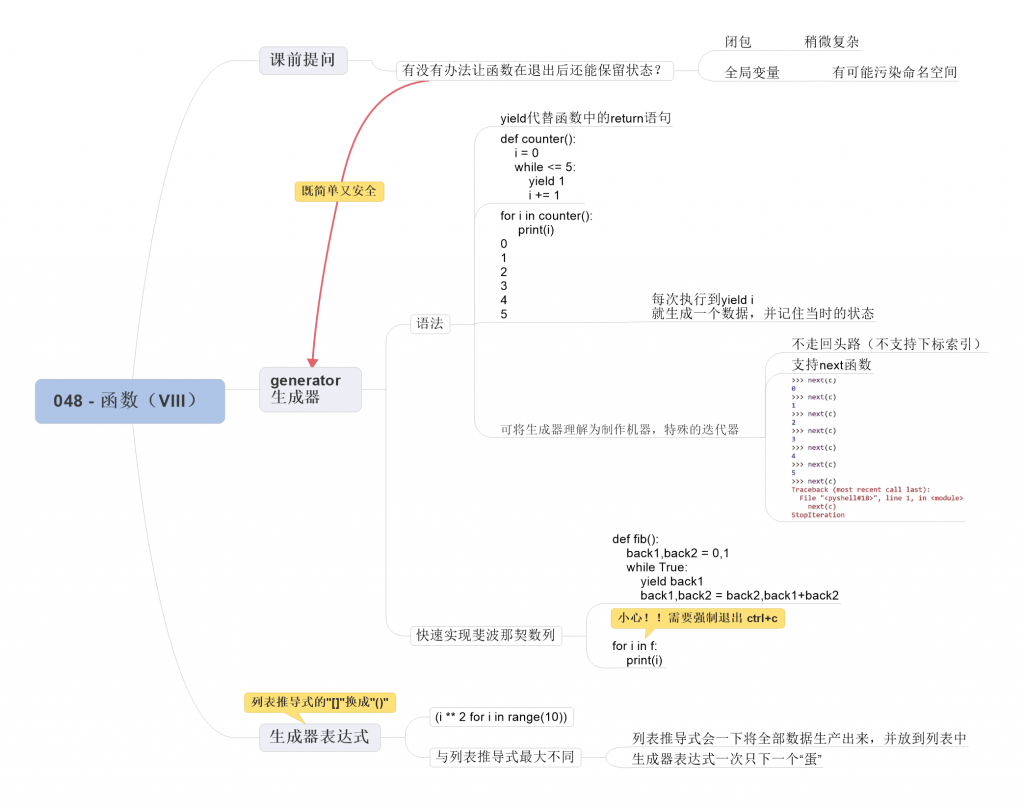
1. 生成器

在 Python 中，使用了 yield 语句的函数被称为生成器（generator）。

与普通函数不同的是，生成器是一个返回生成器对象的函数，它只能用于进行迭代操作，更简单的理解是 —— 生成器就是一个特殊的迭代器。

在调用生成器运行的过程中，每次遇到 yield 时函数会暂停并保存当前所有的运行信息，返回 yield 的值, 并在下一次执行 yield 方法时从当前位置继续运行。

定义一个生成器，很简单，就是在函数中，使用 yield 表达式代替 return 语句即可。
举个例子：

>>> def counter():
... i = 0
... while i <= 5:
... yield i
... i += 1

现在我们调用 counter() 函数，得到的不是一个返回值，而是一个生成器对象：

>>> counter()
<generator object counter at 0x0000025835D0D5F0>

我们可以把它放到一个 for 语句中：

>>> for i in counter():
... print(i)
...
0
1
2
3
4
5

注意：生成器不像列表、元组这些可迭代对象，你可以把生成器看作是一个制作机器，它的作用就是每调用一次提供一个数据，并且会记住当时的状态。而列表、元组这些可迭代对象是容器，它们里面存放着早已准备好的数据。

生成器可以看作是一种特殊的迭代器，因为它首先是 “不走回头路”，第二是支持 next() 函数：

>>> c = counter()
>>> next(c)
0
>>> next(c)
1
>>> next(c)
2
>>> next(c)
3
>>> next(c)
4
>>> next(c)
5
next(c)
Traceback (most recent call last):
File "<pyshell#51>", line 1, in <module>
next(c)
StopIteration

当没有任何元素产出的时候，它就会抛出一个 “StopIteration” 异常。

由于生成器每调用一次获取一个结果这样的特性，导致生成器对象是无法使用下标索引这样的随机访问方式：

>>> c = counter()
>>> c[2]
Traceback (most recent call last):
File "<pyshell#53>", line 1, in <module>
c[2]
TypeError: 'generator' object is not subscriptable

在讲闭包的时候，课后作业留了一道题（梦幻联动），就是让大家利用闭包，来求出斐波那契数列。

那么同样的题目，我们使用生成器来实现，会有多简单呢？

来，看代码：

>>> def fib():
... back1, back2 = 0, 1
... while True:
... yield back1
... back1, back2 = back2, back1 + back2
...
>>> f = fib()
>>> next(f)
0
>>> next(f)
1
>>> next(f)
1
>>> next(f)
2
>>> next(f)
3
>>> next(f)
5
>>> next(f)
8
>>> next(f)
13
>>> next(f)
21

只要我们调用 next(f)，就可以继续生成一个新的斐波那契数，由于我们在函数中没有设置结束条件，那么这样我们就得到了一个永恒的斐波那契数列生成器，薪火相传、生生不息。

2. 生成器表达式

其实在前面讲解元组的时候，小甲鱼就给大家预告了这一章节的到来。

因为列表有推导式，元组则没有，如果非要这么写：

>>> (i ** 2 for i in range(10))
<generator object <genexpr> at 0x0000019A976CC5F0>

那么我们可以看到，它其实就是得到一个生成器嘛：

>>> t = (i ** 2 for i in range(10))
>>> next(t)
0
>>> next(t)
1
>>> next(t)
4
>>> next(t)
9
>>> next(t)
16
>>> for i in t:
... print(i)
...
25
36
49
64
81

这种利用推导的形式获取生成器的方法，我们称之为生成器表达式。

3. 本节思维导图

函数（IX）- 递归

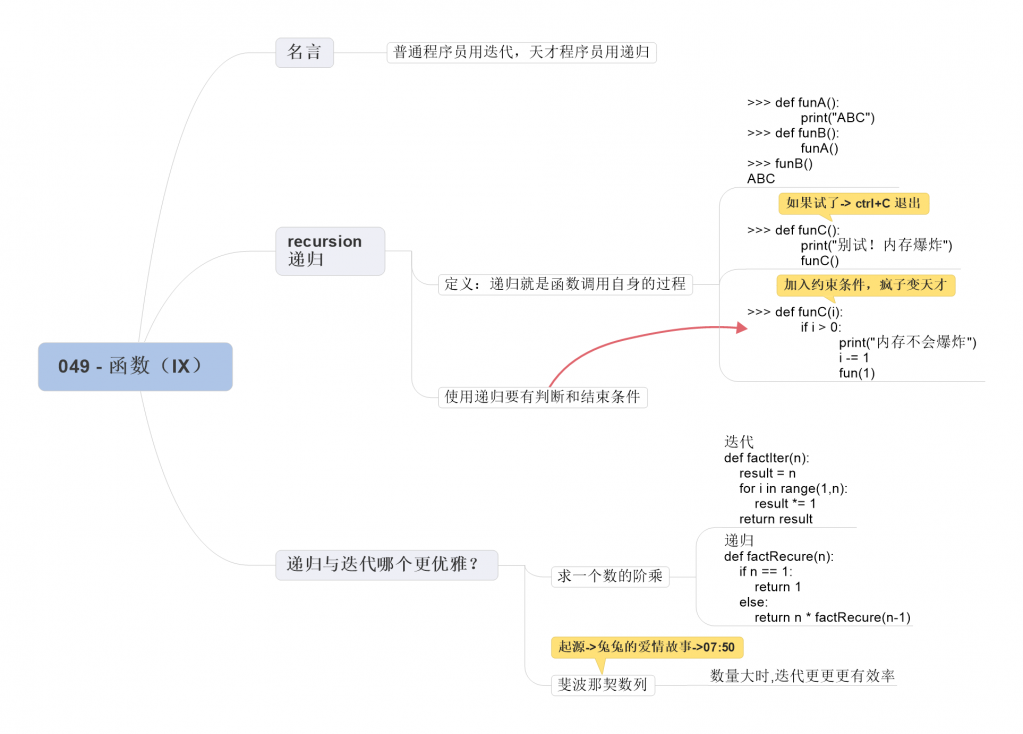
1. 递归

递归就是就是函数调用自身的过程，举个例子：

>>> def funC():
... print("AWBDYL")
... funC()
...
>>> funC()
AWBDYL
AWBDYL
AWBDYL
AWBDYL
AWBDYL
AWBDYL
AWBDYL
AWBDYL
AWBDYL
AWBDYL
...

上面代码会持续输出 “AWBDYL”，直到你把 IDLE 关闭或者使用 Ctrl + c 快捷键强制中断执行。

加上一个条件判断语句，让递归在恰当的时候进行回归，那么失控的局面就得到了控制：

>>> def funC(i):
... if i > 0:
... print("AWBDYL")
... i -= 1
... funC(i)
...
>>> funC(10)
AWBDYL
AWBDYL
AWBDYL
AWBDYL
AWBDYL
AWBDYL
AWBDYL
AWBDYL
AWBDYL
AWBDYL

再次强调一下，要让递归正常工作，必须要有一个结束条件，并且每次调用都将向着这个结束条件推进。

2. 使用递归求一个数的阶乘

一个正整数的阶乘，是指所有小于及等于该数的正整数的积，所以 5 的阶乘是 1×2×3×4×5，结果等于 120。

我们先来试试迭代的实现方法：

>>> def factIter(n):
... result = n
... for i in range(1, n):
... result *= i
... return result
...
>>> factIter(5)
120
>>> factIter(10)
3628800

那么递归来实现的话，代码则是像下面这样：

>>> def factRecur(n):
... if n == 1:
... return 1
... else:
... return n * factRecur(n-1)
...
>>> factRecur(5)
120
>>> factRecur(10)
3628800

3. 使用递归求斐波那契数列

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

首几个斐波那契数是：

1、 1、 2、 3、 5、 8、 13、 21、 34、 55、 89、 144、 233、 377、 610、 987……

我们先来试试迭代的实现方法：

>>> def fibIter(n):
... a = 1
... b = 1
... c = 1
... while n > 2:
... c = a + b
... a = b
... b = c
... n -= 1
... return c
...
>>> fibIter(12)
144

如果使用递归来实现，代码就是这样的：

>>> def fibRecur(n):
... if n == 1 or n == 2:
... return 1
... else:
... return fibRecur(n-1) + fibRecur(n-2)
...
>>> fibRecur(12)
144

4. 本节思维导图

函数（X）- 汉诺塔

汉诺塔其实是 1883 年的时候，由法国数学家卢卡斯发明的。

不过这个游戏呢，与一个古老的印度传说有关：据说在世界中心贝拿勒斯的圣庙里边，有一块黄铜板，上边插着三根宝针。

印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的 64 片金片，这就是所谓的汉诺塔原型。

然后不论白天还是黑夜，总有一个僧侣按照下面的规则来移动这些金片：“一次只移动一片，不管在哪根针上，小片必须在大片上面。”

另外僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、和众生也都将同归于尽。

2. 汉诺塔玩法分解

对于游戏的玩法，我们可以简单分解为三个步骤：

将顶上的 63 个金片从 A 移动到 B
将最底下的第 64 个金片从 A 移动到 C
将 B 上的 63 个金片移动到 C

看着跟没说一样……

那么先让我们把难度简化为婴儿等级 —— 3 个金片：

将顶上的 2 个金片从 A 移动到 B
将最底下的第 3 个金片从 A 移动到 C
将 B 上的 2 个金片移动到 C

第 2 个步骤仍然是一步到位，难点就在于第 1 和第 3 个步骤，不过难度经过降级之后，我们可以简单看出：

第 1 个步骤只需要借助 C，就可以将两个金片从 A 移到 B，第 3 个步骤只需要借助 A，就可以将 2 个金片从 B 移到 C。

于是：

1. 将顶上的 2 个金片从 A 移动到 B 上，确保大片在小片下方

将顶上的 1 个金片从 A 移到 C 上
将底下的 1 个金片从 A 移到 B 上
将 C 上的 1 个金片移动到 B 上

2. 将最底下的第 3 个金片从 A 移动到 C 上

3. 将 B 上的 2 个金片移动到 C 上

将顶上的 1 个金片从 B 移到 A 上
将底下的 1 个金片从 B 移到 C 上
将 A 上的 1 个金片移动到 C 上

3. 汉诺塔代码实现

def hanoi(n, x, y, z):
if n == 1:
print(x, '-->', z) # 如果只有 1 层，直接将金片从 x 移动到 z
else:
hanoi(n-1, x, z, y) # 将 x 上的 n-1 个金片移动到 y
print(x, '-->', z) # 将最底下的金片从 x 移动到 z
hanoi(n-1, y, x, z) # 将 y 上的 n-1 个金片移动到 z
n = int(input('请输入汉诺塔的层数：'))
hanoi(n, 'A', 'B', 'C')

函数（XI）- 函数文档、类型注释、内省

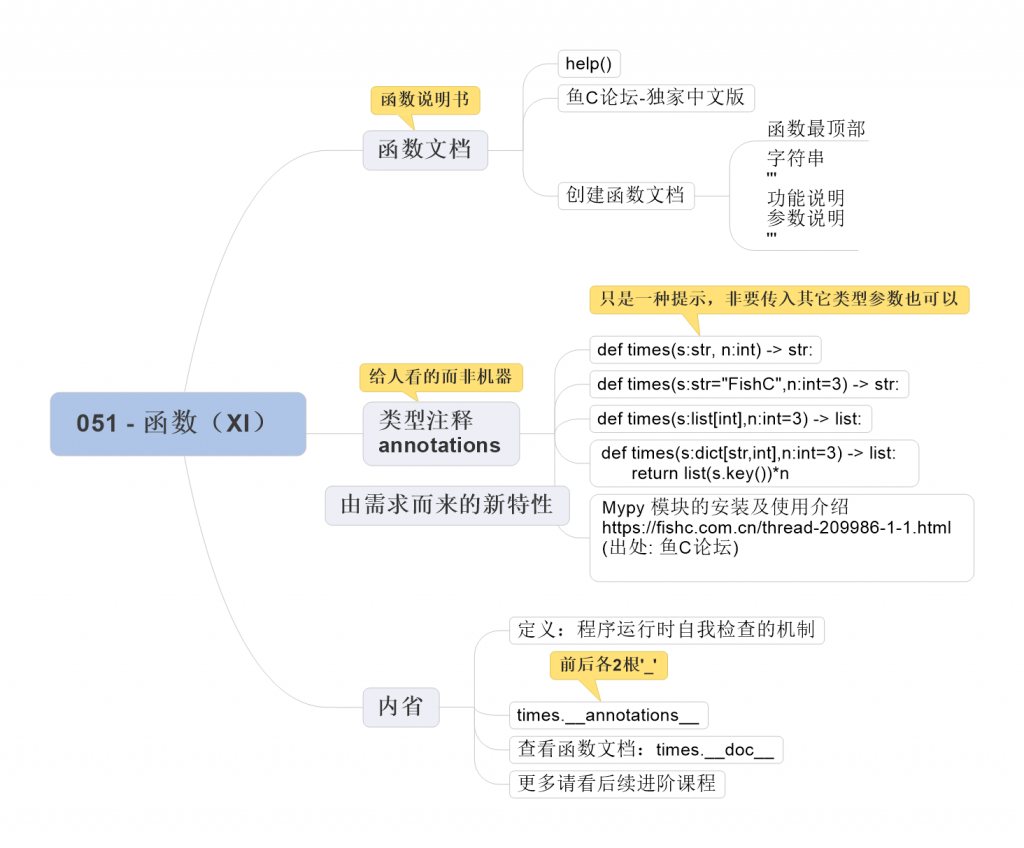
1. 函数文档

使用 help() 函数，我们可以快速查看到一个函数的使用文档：

>>> help(print)
Help on built-in function print in module builtins:
print(...)
print(value, ..., sep=' ', end='\n', file=sys.stdout, flush=False)
Prints the values to a stream, or to sys.stdout by default.
Optional keyword arguments:
file: a file-like object (stream); defaults to the current sys.stdout.
sep: string inserted between values, default a space.
end: string appended after the last value, default a newline.
flush: whether to forcibly flush the stream.

创建函数文档非常简单，使用字符串就可以了，举个例子：

>>> def exchange(dollar, rate=6.32):
"""
功能：汇率转换，美元 -> 人民币
参数：
- dollar 美元数量
- rate 汇率，默认值 6.32（2022-03-08）
返回值：
- 人民币数量
"""
return dollar * rate
...
>>> exchange(20)
126.4

注意：函数文档一定是在函数的最顶部。

我们可以看到，函数开头的几行字符串并不会被打印出来，但它将作为函数的文档被保存起来。

现在通过 help() 函数，就可以查看到 exchange() 的文档了：

>>> help(exchange)
Help on function exchange in module __main__:
exchange(dollar, rate=6.32)
功能：汇率转换，美元 -> 人民币
参数：
- dollar 美元数量
- rate 汇率，默认值 6.32（2022-03-08）
返回值：
- 人民币数量

2. 类型注释

有时候，你可能会看到这样的代码：

>>> def times(s:str, n:int) -> str:
... return s * n

其实这里面多出来的东东，就是 Python 的类型注释啦~

比如上面代码表示该函数的作者，希望调用者传入到 s 参数的是字符串类型，传入到 n 参数的是整数类型，最后还告诉我们函数将会返回一个字符串类型的返回值：

>>> times("FishC", 5)
'FishCFishCFishCFishCFishC'

当然，这只不过是函数作者的寄望，如果调用者非要胡来，Python 也是不会出面阻止的：

>>> times(5, 5)
25

因为这只是类型注释，是给人看的，不是给机器看的哈。

如果需要使用默认参数，那么类型注释可以这么写：

>>> def times(s:str = "FishC", n:int = 5) -> str:
... return s * n
...
>>> times()
'FishCFishCFishCFishCFishC'

如果期望的参数类型是列表，可以这么写：

>>> def times(s:list, n:int = 5) -> list:
... return s * n
...
>>> times([1, 2, 3], 3)
[1, 2, 3, 1, 2, 3, 1, 2, 3]

如果还想更进一步，比如期望参数类型是一个整数列表（也就是列表中所有的元素都是整数），那么代码可以这么写：

>>> def times(s:list[int], n:int = 5) -> list:
... return s * n

映射类型也可以使用这种方法，比如我们期望字典的键是字符串，值是整数，可以这么写：

>>> def times(s:dict[str, int], n:int = 5) -> list:
... return list(s.keys()) * n
...
>>> times({'A':1, 'B':2, 'C':3}, 3)
['A', 'B', 'C', 'A', 'B', 'C', 'A', 'B', 'C']

3. mypy

Mypy 模块的安装及使用介绍 -> 传送门

4. 内省

内省，其实最先是心理学的基本研究方法之一，又称为自我观察法。它是发生在内部的，我们自己能够意识到的主观现象。

Python 通过一些特殊的属性来实现内省，比如我们想知道一个函数的名字，可以使用 __name__：

>>> times.__name__
'times'

使用 ___annotations__ 查看函数的类型注释：

>>> times.__annotations__
{'s': dict[str, int], 'n': <class 'int'>, 'return': list[str]}

查看函数文档，可以使用 __doc__：

>>> exchange.__doc__
'\n\t功能：汇率转换，美元 -> 人民币\n\t参数：\n\t- dollar 美元数量\n\t- rate 汇率，默认值 6.32（2022-03-07）\n\t返回值：\n\t- 人民币数量\n\t'

阅读不友好，咱们使用 print() 函数给打印一下：

>>> print(exchange.__doc__)
功能：汇率转换，美元 -> 人民币
参数：
- dollar 美元数量
- rate 汇率，默认值 6.32（2022-03-07）
返回值：
- 人民币数量
>>>

5. 本节思维导图

函数（XII）- 高阶函数

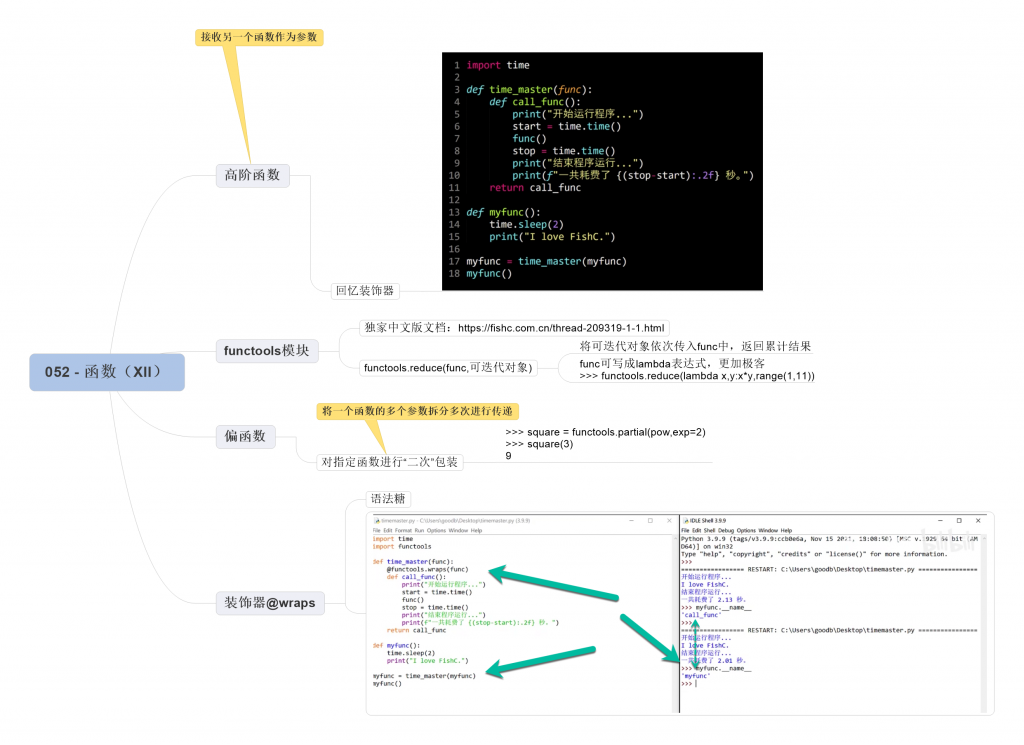
1. 高阶函数

很多同学一听高阶，那一定是很厉害很强大的意思，其实这样描述并不全面。

在前面的学习中，我们发现，函数是可以被当作变量一样自由使用的，那么当一个函数接收另一个函数作为参数的时候，这种函数就称之为高阶函数。

高阶函数几乎就是函数式编程的灵魂所在，所以 Python 专程为此搞了一个模块 —— functools，这里面包含了非常多实用的高阶函数，以及装饰器。

友情提示，这是好东西，一定要收藏 -> functools -- 高阶函数

2. reduce() 函数