目录
4.判定解的情况,单纯求r(A),r(A,b)的过程行列变换都可
本节是线代某些知识点总结,可能较零碎。
对于简单的知识点,例如“两行对应成比例,行列式为0"就不讲了。暂时不举例题,有时间会继续补充!
一.初等行/列变换
1.计算行列式时,行列变换都可
因为,所以不论动行/列都是等价的。
变换规则:
1.“倍乘”:行列式的某行(列)乘某个元素k。相应的,若行列式中某行(列)元素有公因子k(k≠0),则k可提到行列式外面,即:
2."互换":行列式中两行(列)互换,行列式变号。
3.“倍加”:某行(列)的k倍加到另一行(列),行列式不变。
2.求矩阵的秩时,行列变换都可
因为初等变换不改变某个矩阵非零子式的最高阶数,秩指的就是非零子式的最高阶数。
初等变换的规则:
1."倍乘":一个非零常数乘矩阵矩阵的某一行(列)。
2."互换":互换矩阵中某两行(列)的位置。
3."倍加":将矩阵的某一行(列)的k倍加到令一行(列)。
注意:
某矩阵乘元素k,是矩阵中的每个元素都成k,要与行列式区分。
也就是
。
3.解线性方程组时,仅能使用初等行变换
因为矩阵的每一种初等行变换都对应着线性方程组的同解变换,而作列变换会改变原来的方程。

4.判定解的情况,单纯求r(A),r(A,b)的过程行列变换都可
注:将r(A,b)化行阶梯求秩时,往往我们需要同时得到r(A),如果想用列变换的话,只能对A单独列变换,千万不要将b列和A的列混合运算,这样r(A)就不准了。(但r(A,b)是准的)。

但是,如果涉及到求通解或唯一解,那么就只能做行变换化行阶梯了,所以建议一开始就只做行变换。
总结:求解的过程,就只进行初等行变换化行阶梯求秩,并且顺势化为行最简型求解。
5.求向量组极大无关组、线性表出关系,则仅行变换
因为初等行变换不改变列向量组的线性表出关系。例如下图,矩阵中,
,
矩阵同样有这样的关系。

6.求向量组的秩时,行列变换都可
求向量组的秩,其实最后会转化为求矩阵的秩,原理就是"矩阵的秩=行向量组的秩=列向量组的秩",所以求向量组的秩也是行列变换都可。
![]()
但是一般求向量组的秩后面会继续求解极大无关组/线性表出关系,这时只能做行变换,所以还是建议从开头就只使用行变换。
7.求特征值时,行列变换都可
因为特征多项式本质上是行列式,求行列式时,行列都可以换。
![]()
8.求特征向量时,仅做行变换
因为求特征向量时,本质是在解线性方程组,只能进行初等行变换。

9.求逆矩阵时,对(A,E)仅做初等行变换
因为以左乘A得到E,以
左乘E得到
,以
左乘的过程就是做初等行变换的过程。

所以怎么体现A和E做了完全一样的所带来的初等行变换,就是将A,E横着拼在一起,此时做的初等行变换就是同步的了。
![]()
总结:
除了① 求行列式的值(求特征值本质上就是求行列式的值)和 ② 单纯求秩,行列变换都可,其余情况通通只做行变换。
二.要牢记

一些推导:

对于AB ≠ BA的补充:

在AB≠BA的情况下,只能写成

1.矩阵的逆

推导如下:

初等矩阵的逆:
2.矩阵的伴随

三.某某子式
1.余子式
在n阶行列式中,去掉元素a所在的第i行、第j列元素,由剩下的元素按原来的位置与顺序组成的n-1阶行列式称为元素a的余子式,记作。
2.代数余子式
余子式乘
后称为a的代数余子式,记作A

3.k阶子式
给定一个矩阵,任取k行,任取k 列,共个数构成的行列式,出现在矩阵的秩中,定义如下:
设A是mxn矩阵,则若存在k阶子式不为零,而任意k+1阶子式(如果有的话)全为零,则r(A)=k,且若A为nxn矩阵,则:

4.k阶主子式
指在行列式中选k行k列,但要求行和列的下标相同。如:行为r1、r2、r3,列必须为c1、c2、c3;行为r2、r3、r5,列必须为c2、c3、c5。因此,k阶主子式不唯一。
这在矩阵相似会用到,下面会讲。
5.顺序主子式
顺序主子式是在主子式上再加限定,顺序主子式是由 1~k 行和 1~k 列所确定的子式。
例如:
1阶时:取第1行,第1列
2阶时:取第1、2行,第1、2列
3阶时:取第1、2、3行,第1、2、3列
4阶时:取第1、2、3、4行,第1、2、3、4列
实际上,主子式的主对角线元素是原 n 阶行列式的主对角线元素的一部分,且顺序相同。
所以k 阶主子式是不唯一的,而 k 阶顺序主子式是唯一的。
用在判断二次型正定上,下面会讲。
四.矩阵的秩
① 0 <= r(A) <= min{m,n}
② r(kA)=r(A)(k ≠ 0)
③ r(AB) <= min{r(A),r(B)}
④ r(A+B) <=r(A)+r(B)
⑤

r(A)=n-1,r(A*)=1的证明:

进而可得出一个重要结论:
,则r(A)+r(B)<=n
所以,看到A*B就要想到两个结论:

⑥ 设A是m*n矩阵,P,Q分别是m阶,n阶可逆矩阵,则
r(A)=r(PA)=r(AQ)=r(PAQ)
⑦ r(A)==r(
)=r(
)
关于⑤的例题:

为什么Ax=b有n-r+1个线性无关的解:

五.常用特征值与特征向量

针对
,如果知道B的特征值和特征向量,想要反求A的特征值特征向量,结论:
特征值不变,特征向量为P
证明过程:
注意这样一道例题:




关于特征值的一些提示:

六.矩阵,向量组,方程组
矩阵,向量组
① 向量组是由有限个相同维数的行向量或者列向量组成,其中向量是由n个实数组成的有序数组,是一个n*1的矩阵(n维列向量)或是一个1*n的矩阵(n维行向量)。
② 矩阵是由m*n个数排列成m行n列的数表。
一个向量组可以看作是一个矩阵的列(或行)向量集合。如果一个矩阵有n列,那么这n列就可以看作是一个由n个向量组成的向量组。反过来,一个矩阵也可以看作是由其列(或行)向量组成的向量组。
1.怎么判断两个矩阵等价
矩阵等价的前提:A与B是同型矩阵,即A,B行数,列数相同
矩阵等价的充要条件:
① r(A)=r(B)
② PAQ=B,P,Q可逆
2.怎么判断两个向量组是等价向量组
向量组等价的前提:A,B矩阵同维
若r( Ⅰ )=r(
....) r(Ⅱ)=r(
....)
向量组等价的充要条件:
① r(Ⅰ)=r(Ⅱ),且(Ⅰ)可由(Ⅱ)线性表出(单向表出即可)② r(Ⅱ)=r(Ⅰ),且(Ⅱ)可由(Ⅰ)线性表出(单向表出即可)
③ r(
....) =r(
....) =r(
...,
...),即
r(Ⅰ)=r(Ⅱ)=r(Ⅰ,Ⅱ)
④ Ⅰ和Ⅱ能够相互线性表示。
总结:
① 两个矩阵A与B等价指的是A可以通过有限次初等变换变成B。两个不同型矩阵是不可能等价
乡
② 两个向量组等价只指的是它们能够互相线性表示,它们各自所含向量的个数可能是不一样的。③ 两个向量组等价,一个线性无关,另一个不一定线性无关。
例题:

D.即使Ⅰ 和 Ⅱ 同为n维向量组,但是s与t的关系未知,也就是行数相等,列数未知,所以A,B两个矩阵可能不同型,不能等价。
B.(Ⅰ)可由(Ⅱ)表示,缺少其他条件,如果① 加上(Ⅱ)可由(Ⅰ)线性表出 或者② r(Ⅰ)=r(Ⅱ)就对了
C正确
D r(A)=r(B),只能推出两个向量组秩相同,缺少其他条件,如果加上① 加上(Ⅱ)可由(Ⅰ)线性表出 或者②加上(Ⅰ )可由(Ⅱ)线性表出或者③ r(Ⅰ)=r(Ⅱ)=r(Ⅰ,Ⅱ),就对了。

3.矩阵和向量等价的比较

例题:
A.(
)能与(
)相互线性表示,但是(
)不是Ax=0的基础解系
B.基础解系一定是线性无关的,但是B选项3个向量是线性相关的(3个向量相加=0)
C.像上面举的例子一样,
,
等秩,但是
与
不能相互线性表示。
D.
在(
)的右边乘可逆矩阵,不改变原来矩阵的秩,且(
)与(
)能相互线性表示
所以,求Ax=0的另一个基础解析,需要满足与(
)等价且等秩。
4.同解方程组
若两个方程组与
有完全相同的解,则称它们为同解方程组
充要条件:
① Ax=0的解满足Bx=0,且Bx=0的解满足Ax=0(互相把解代入求出结果即可)
② r(A)=r(B),且Ax=0的解满足Bx=0(或Bx=0的解满足Ax=0)
③ r(A)=r(B)=r(
)(三秩相同)

如果是齐次线性方程组,那么A,B是同解方程组,若是非齐次那么就不对了。
例1:

例2:

例3:

七.齐次线性方程组和非齐次线性方程组
齐次线性方程组有解的条件:
① r(A)=n时,方程组有唯一零解。
② r(A)=r<n时,方程组有非零解(无穷多解),且有n-r个线性无关解
齐次方程组其实就是解和系数的正交,例如,给你一个条件:
---->
则(1 -2 -1 0)就是齐次方程组的基础解系
非齐次线性无关组有解的条件:
① 若r(4)≠r([A,b]),则方程组无解;
② 若r(A)=r([A,b])=n,则方程组有唯一解;
③ r(A)=r([A,b])=r<n,则方程组有无穷多解。
非齐次方程组的通解的求法:
①求Ax=0的解
② 求Ax=b的一个特解
③ 非齐次方程组的通解=齐次方程组的解+一个非齐次的特解

如果A行满秩,则r(A)=r(A|b),那么方程组一定有解。
如果A列满秩,则r(A)与r(A|b)的关系不确定:
① r(A)<r(A|b),则无解
② r(A)=r(A|b)<n,有无穷多解
③ r(A)=r(A|b)=n,有唯一解
非齐次方程组解的性质:
若
是非齐次线性方程组Ax=b的解,
是对应齐次方程组Ax=0的解,则:
(1)是Ax=0的解;(2)
是Ax=b的解
扩展:

解释:
1.p个解的任意组合,都是齐次线性方程组的解
2.非齐次的解线性组合也能得到齐次线性方程组的解,但是需要满足k1+k2+...+kp=0,例如,
=0(1-1=0),
就是齐次线性方程组的解。
3.非齐次的解线性组合也能得到非齐次线性方程组的解,但是需要满足k1+k2+...+kp=1,例如,
,就是非齐次线性方程组的一个解。
4.齐次线性方程组的解与非齐次线性方程组的解相加,得到的是非齐次线性方程组的解。
5.r(A)=r,A就有n-r个线性无关的解,而x1,x2,....
刚好是Ax=0的n-r个线性无关解,所以
k1x1+k2x2+....+
是Ax=0的解。
例题:

A.
是组合系数是1-1=0,
是Ax=0的解
B.
是Ax=b的解,C,D同理。
八.对比记忆
1.
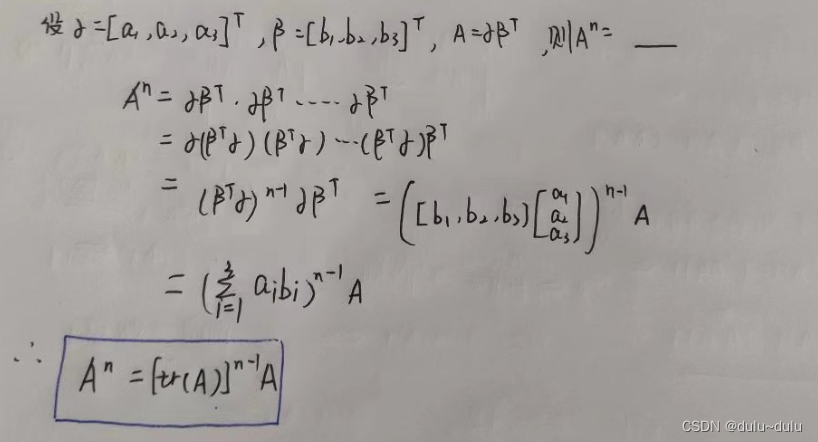
矩阵A的tr(A):tra(A)=矩阵A的迹=对角线元素之和
2.对于秩为1的n阶矩阵A或A=(或
)(a,β都是n维非零列向量),其特征值为
=0,
(或
)

3.

例题1:

例题2:

九.相似与正交
存在n阶可逆矩阵P,使得,则称A相似于B,记为A~B
若A~B
① |A|=|B|
② r(A)=r(B)
③ tr(A)=tr(B)
④
(
)
⑤
⑥ A,B各阶主子式之和分别相同
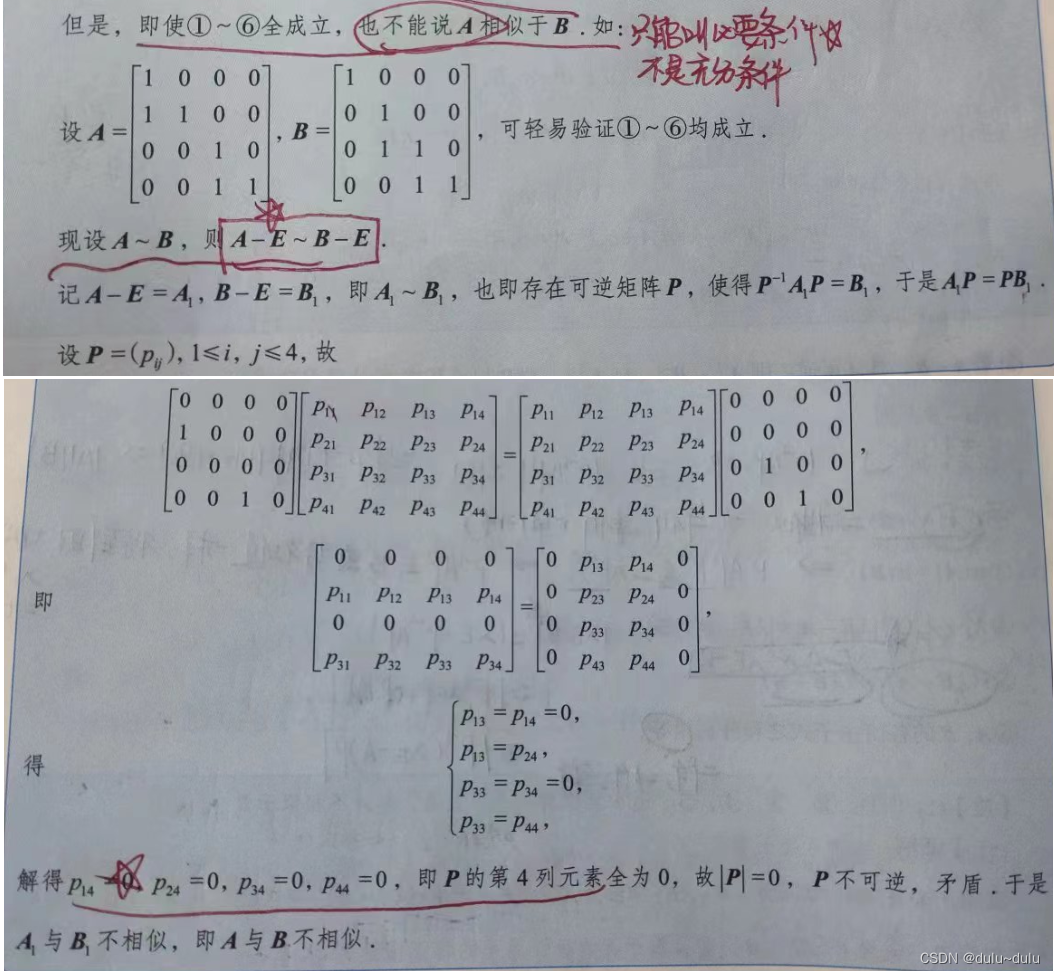
也就是说,A与B即使特征值相同,但也不一定相似。但是如果A,B都是实对称矩阵,那么相似,则一定特征值相同(实对称矩阵一定能相似对角化,特征值相同一定能相似于同一个对角矩阵,根据传递性A~B)。
那么怎么判定矩阵相似呢?
① 定义法
存在n阶可逆矩阵P,使得
② 传递法
A~
,
~B,则A~B,其中
为对角阵
这就要说到矩阵的相似对角化
矩阵可相似对角化的条件:
充要条件:
① n阶矩阵A可相似对角化↔有n个线性无关的特征向量。
② n阶矩阵A可相似对角化↔A对应于每个k重特征值都有k个线性无关的特征向量
必要条件:
③ n阶矩阵A有n个不同特征值→A可相似对角化
④ n阶矩阵为实对称矩阵→A可相似对角化
对于矩阵相似对角化的步骤:
① 求特征值
② 求特征向量
③ 正交化(如果需要的话),单位化
④ 令Q=[
],则Q为正交矩阵,且
上面提到了实对称矩阵,实对称矩阵就是组成A的元素都是实数。对于实对称矩阵()要记住:

对于正交,你需要记住:
①,则
,
是正交向量
② 若满足
,则A是正交矩阵
↔
③ 若A为正交矩阵,则
为正交矩阵,
为正交矩阵,
为正交矩阵,-A为正交矩阵
④ 若A,B为同阶正交矩阵,则AB为正交矩阵,A+B不一定为正交矩阵
⑤ 若A为正交矩阵,则其特征值的取值范围为{-1,1}
在易错知识点有补充。
例题:

不可对角化的矩阵怎么判断相似:
例题:

如果A与B相似,那么:
对于任意实数k和整数n,有
与
相似
对于上面这道题,取k=-1,n=1,判断哪两个矩阵相似。
矩阵相似还可得出:
① A~B,
,f(A)=f(B)
② 若A~B,且A可逆,则
~
,f(
)=f(
)
③ 若A~B,
~
④ 若A~B,
~
注:
提醒:

再次提醒,矩阵等价怎么判定:
设A,B均为m*n矩阵,若存在可逆矩阵Pm*n,Qm*n,使得PAQ=B,则A,B是等价矩阵。若A,B是同型矩阵,则A与B等价的充分必要条件是r(A)=r(B)
十.实对称矩阵
实对称矩阵中不同特征值对应的特征向量相互正交。

实对称矩阵可以用正交矩阵相似对角化,这是必然的。

要与合同区别,合同:对于实对称矩阵A,必存在可逆矩阵C,使得
AC=
,
对角矩阵,这里的C不是A的特征向量,
也不是A的特征值。
若普通矩阵能相似对角化,能不能用正交矩阵相似对角化?
对于n阶实对称矩阵,n个线性无关的特征向量即使不正交,也可以通过施密特正交实现正交化,再单位化得到正交矩阵。那普通矩阵可以相似对角化,他也有n个线性无关的特征向量,其特征向量是否可以正交化,单位化,再用得到的正交矩阵Q进行相似对角化?
答案是否定的。

1.A为n阶实对称矩阵的充分必要条件为:A有n个正交的特征向量。

为什么不能是普通矩阵
例题:

2.A为实对称矩阵的则A*为实对称矩阵,反过来不对。

十一.合同
设A,B为n阶矩阵,若存在可逆矩阵C,使得,则称A与B合同,即
。A与B合同,就是指同一个二次型在可逆线性变换下的两个不同状态的联系。



注:由于我们已经规定,对称矩阵才是二次型矩阵,所以二次型矩阵都是对称矩阵,相应的和对称矩阵合同的矩阵也是对称矩阵。
例题:




十二.二次型
关于二次型化标准型或规范型的方法:配方法,正交变化有总结如下:

所以我们可以进一步得到
等价,合同和相似的关系:

注:相似一定合同的前提条件是A,B都是实对称矩阵

例题:




关于配方法和正交变换分别给一个例题:
配方法:

正交变换:


① 若
,那么两个同一特征值对应的特征向量需要正交化,如果本来就正交可以不做这一步,所以在计算特征值的时候,可以将两个特征向量写为正交的,这样就免去了施密特正交化,直接进入单位化即可。
②
,那么不用进行施密特正交,直接单位化即可。
常见题型:
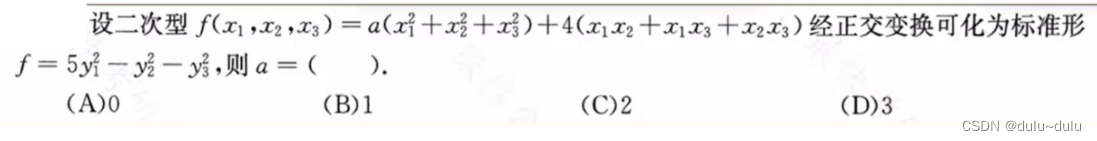

这里记录一个例题:


若二次型中只有混合项,没有平方项,要怎么做?

两类典型大题:【线代救命#6】一个视频彻底搞懂二次型 !!_哔哩哔哩_bilibili
如果两个矩阵相似,那么可以直接用标准型作为桥梁,无需化为规范型:

如果两个矩阵不相似,那么只能用规范型作为桥梁,因为两个矩阵合同,规范型是唯一的:
十三.二次型正定
二次型正定的充要条件:
n元二次型正定↔对任意x≠0,有
>0(定义)
① ↔f的正惯性指数p=n
② ↔存在可逆矩阵D,使得
③ ↔
,A与E合同
② ③推导:
④↔A的特征值
>0
⑤↔A的全部顺序主子式>0
二次型正定的必要条件:
①
>0,对角线元素全部大于0
② |A|>0
最好是使用充要条件① ④ ⑤判断二次型是否正定,如果非要用定义法,来看个例题:

注意上题,不能直接将f判定为正定:
因为将二次型化为标准型的过程一定要做可逆线性变换

例题1:


例题2:




看到这种平方和形式的二次型,要想到他一些性质:
平方和形式的二次型(重要):


例题:

答案C,由于二次型矩阵正定,则r(B)满秩,进而推出|B|≠0

注意一定要是平方和,下面这个就不是,就只能用开头讲的特征值法,配方法和合同变换:

关于正定的重要结论:


十四.秩1矩阵的性质(重要)
假设A是一个秩为1的矩阵,
与
为列向量,且
=
=A
1.如果一个矩阵能由一个列向量*一个行向量表示,那么这个矩阵秩一定为1,即r=1。同样,一个秩为1的矩阵,可以拆成一个列向量*一个行向量,并且表示方法不唯一。
2.矩阵A的迹(对角线的和)=
=
,也就是内积
同时,|A|=对角线元素的乘积
3.A的特征值为
=tr(A),其余特征值全部为0
4.A的特征向量:
对于
=tr(A)对应的特征向量:
A=
--->
=tr(A)*
,所以
=tr(A),特征向量为k
,k
0
也就是说
=tr(A)对应的特征向量是组成A矩阵前面的列向量。
对于
对应的特征向量:
--->
,即求AX=0的齐次解,就是
对应的特征向量
5.tr(A)是1重特征值,0是n-1重特征值
① tr(A)
0
=n-r(A)=n-1,所以当tr(A)
0时,秩1矩阵一定能相似对角化
① tr(A)=0,这时0是n重特征值:
=n-r(A)=n-1≠n,所以不能相似对角化
6.
例题1:

例题2:

补充:其他特殊矩阵
幂0矩阵:3阶矩阵:,4阶矩阵:
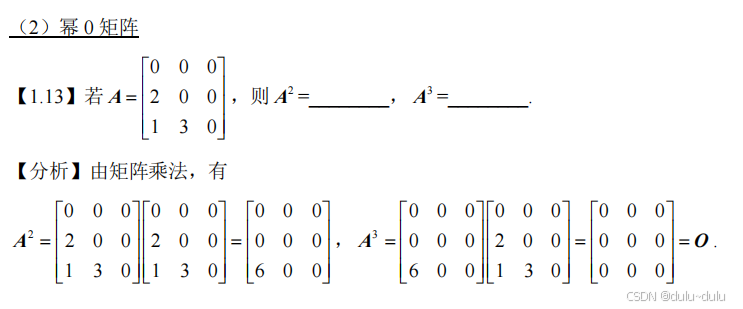

![]()

十五.关于aB+Ba(重要)


十六.同解和向量组等价


首先排除A,C,只有行向量才和方程组的解有关系。由于A可由B线性表出,B更具有代表性,约束更多,D正确。

注:列向量组等价不能推出同解,行向量组等价才能推出同解。
经过列变换,列向量组等价,但此时方程组的结构已经发生改变,所以解方程组只能行变换。
行向量组等价是向量组等价与方程通解的桥梁。


24年数二:

由方程组 Ax=0的解均是BTx=0的解,得Ax=0与
x=0通解。利用r(A)=r
就很好做
十七.从A--->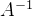 原理
原理
A和E同时做初等行变换,在A化作E的同时,E

例题:


A经过一系列初等行变换可变为下三角矩阵,而变化的过程就被记录在了画圈圈的部分,即画圈圈部分为p

再经过初等列变换,可使PAQ为对角矩阵
十八.分块矩阵的初等变换
①
② 做行变换时左乘,做列变换时右乘。
③
例题:




十九.看到就要想到

对于(1)补充一点,记住即可。

(4)的证明如下:

补充:
1.
Aij=aij--->A*=


Aij+aij=0--->A*=

除此之外,还能得到A是一个正交矩阵:
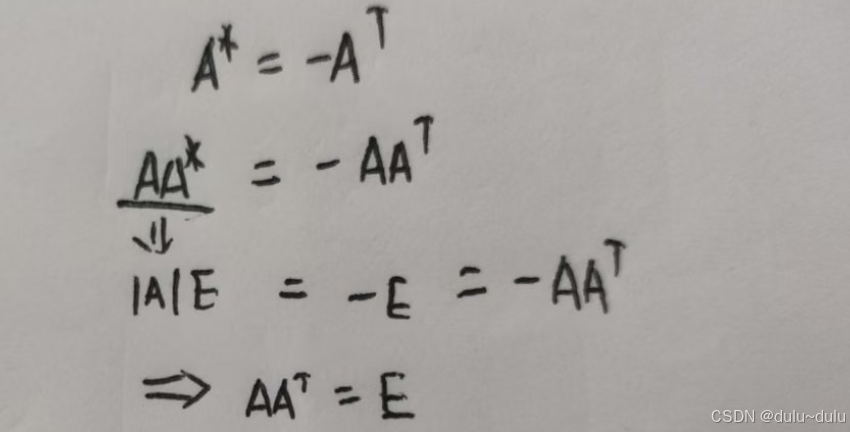

①
,所以A与B一定等价,且合同
② 看了上面,这里不告诉我们P可逆,我们也应该知道P矩阵可逆。
,P是正交阵,所以A与B相似。
2.
以下两题来自:
【线代救命#5】一个视频带你拿捏矩阵相似,出题老头汗流浃背!_哔哩哔哩_bilibili

看这题需要直到,正交矩阵Q的特征值只能是1或-1({-1,1})

3.
求A*x=0的全部解:

对应这道题:

4.A与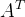 特征值不同,特征向量正交(重要)
特征值不同,特征向量正交(重要)

相似地,可以证明实对称矩阵不同特征值对应地特征向量相互正交。

5.A可相似对角化

答案:D

6.AB与BA的非零特征值相同。

由于AB与BA的非零特征值相同,所以AB的其中两个特征值为1,1
又因为:
所以答案:1,1,0
二十.易错


分块矩阵
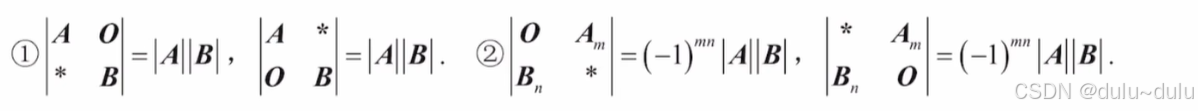
分块矩阵转置

分块矩阵求逆:副对角线求逆,分别求逆,并且对调

主副对角线求逆:

二阶求伴随:主对调,副变号

这里应该是AB=0不能推出A=0或B=0

做题常犯错误:

1.虽然的特征值与A相同,但特征向量不再是
,要单独计算才能得出,要求
的特征值,只能先将A转置,然后再求特征值。

但是有一个性质:
与A属于不同特征值的特征向量正交。

2.=1,
=
1,只能说A的特征值取值范围是{1,-1}

所以进一步可以解释这一段:
若A为正交矩阵,则其特征值的取值范围为{-1,1}

25合工大卷五9:

答案:B
补充:
反对称矩阵的性质

有错欢迎评论区指正!❤️❤️❤️











































 3781
3781

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








