序列决策问题（Sequential Decision-Making Problem）

序列决策问题（Sequential Decision-Making Problem）是强化学习（Reinforcement Learning, RL）的核心研究内容，其核心思想是：​​智能体（Agent）需要在连续的时间步骤中，通过与环境（Environment）的交互，选择一系列动作（Actions），以最大化长期累积奖励（Cumulative Reward）​​。

---

​​1. 序列决策问题的定义​​

在序列决策问题中：

• ​​动态性​​：每个动作的选择不仅影响当前奖励，还会影响后续状态（State）和未来的奖励。
• ​​目标​​：找到一种策略（Policy），使得从初始状态开始，所有时间步的期望累积奖励最大化。
• ​​数学形式​​：通常建模为马尔可夫决策过程（Markov Decision Process, MDP），这是RL的标准框架。

---

​​2. 关键要素​

序列决策问题通过​​马尔可夫决策过程（MDP）​​形式化，包含以下要素：

1. ​​状态空间（State Space, S)​​：环境可能的所有状态集合。
2. ​​动作空间（Action Space, A)​​：智能体可执行的动作集合。
3. ​​转移函数（Transition Function, T)​​：T(s,a,s′)=P(s′∣s,a)，表示在状态s执行动作a后转移到状态s′的概率。
4. ​​奖励函数（Reward Function, R)​​：R(s,a,s′)表示从状态s执行动作a转移到s′获得的即时奖励。
5. ​​折扣因子（γ∈[0,1))​​：用于权衡当前奖励与未来奖励的重要性。

---

​​3. 策略（Policy）与价值函数（Value Function）​​

• ​​策略（π​​）：定义智能体在状态s下选择动作的规则。
  • 确定性策略：π(s)→a。
  • 随机策略：π(a∣s)表示在状态s选择动作a的概率。
• ​​价值函数​​：
  • ​​状态价值函数（Vπ(s)​​）：在状态s下遵循策略π的期望累积奖励。
  • ​​动作价值函数（Qπ(s,a)​​）：在状态s执行动作a后遵循策略π的期望累积奖励。

---

​​4. 核心挑战​​

序列决策问题的难点在于：

1. ​​探索与利用（Exploration vs. Exploitation）：

   • ​​探索​​：尝试新动作以发现潜在的高奖励路径。
   • ​​利用​​：根据已有知识选择当前最优动作。
   • 平衡两者是RL算法的核心挑战（例如通过ε-greedy策略或UCB方法）。

2. ​​延迟奖励（Delayed Reward）​​：

     当前动作的影响可能在多个时间步后才显现（例如围棋中某一步可能决定最终胜负）。

3. ​​高维状态空间​​：

     实际应用中状态可能是高维的（如图像输入），需借助深度神经网络进行函数逼近。

---

​​5. 解决方法​​

​​5.1 基于值函数的方法（Value-Based Methods）​​

• ​​Q-Learning​​：
  • 通过更新动作价值函数Q(s,a)逼近最优策略。
  • 贝尔曼方程（Bellman Equation）是理论基础：
  • 深度Q网络（DQN）使用神经网络拟合Q函数。

​​5.2 基于策略的方法（Policy-Based Methods）​​

• ​​策略梯度（Policy Gradient）​​：
  • 直接优化策略πθ​(a∣s)的参数θ。
  • 通过梯度上升最大化期望累积奖励：

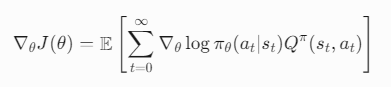
​​5.3 模型基方法（Model-Based Methods）​​

• ​​学习环境模型​​：
  • 估计转移函数T和奖励函数R，通过规划（Planning）生成策略。
  • 适用于数据稀缺或安全性要求高的场景（如机器人控制）。

---

​​6. 实际应用​

• ​​游戏​​：Atari游戏（DQN）、围棋（AlphaGo）、德州扑克（Pluribus）。
• ​​机器人​​：机械臂控制（Model-Based RL）、自动驾驶（在线学习）。
• ​​资源管理​​：智能电网调度、计算资源分配。

---

​​7. 当前研究方向​​

• ​​泛化性​​：如何使策略在未见过的环境中有效。
• ​​样本效率​​：减少与环境交互的次数。
• ​​多智能体系统：多个智能体协作或竞争。

---

​​总结​​

序列决策问题是强化学习的核心，其复杂性源于动态性、延迟奖励和高维状态空间。通过结合深度学习（如DQN、策略梯度）和经典RL理论（如贝尔曼方程），深度强化学习（Deep RL）在复杂任务中取得了突破性进展。