近端策略优化（PPO）总结-CSDN博客

本文链接：https://blog.csdn.net/weixin_71288092/article/details/147494914

PPO 原理通俗讲解

想象你在训练一只狗学技能，比如接飞盘。强化学习的目标是让狗通过试错找到最佳策略，而PPO（近端策略优化）就是一种让训练更稳定、更高效的“驯狗秘籍”。以下是它的核心思想：

1. 基础设定：策略与奖励

策略（Policy）：狗的大脑，决定了它在不同情况下该做什么动作（比如跳多高、跑多快）。我们用神经网络（Actor）模拟这个策略。
奖励（Reward）：每次动作后，主人给出反馈。接到飞盘奖励+10，没接到-5。目标是让狗最大化长期累积奖励。

2. 传统策略梯度的问题

直接更新策略：如果狗某次跳得很高接到了飞盘，传统方法会让它更频繁地跳高。但问题来了：
- 步子太大容易翻车：如果某次跳高成功是运气好，下次策略可能改得太激进，导致后续表现崩盘。
- 数据浪费：每更新一次策略，就要重新试错收集数据，效率低下。

3. PPO的改进：限制策略更新的幅度

PPO的核心思想是：“小步快跑，别浪”。每次更新策略时，确保新策略和旧策略的差距不能太大，避免翻车。具体实现方式有两种：

方法一：KL散度约束（PPO1）

KL散度：衡量新旧策略的差异程度，类似“新旧动作的相似度”。
更新规则：在优化时，强制新旧策略的KL散度不超过某个阈值（比如0.01）。相当于告诉狗：“你可以改进动作，但别改得亲妈都不认识。”

方法二：概率比剪裁（PPO2，更常用）

概率比：新策略选择某个动作的概率 / 旧策略选择该动作的概率。
- 如果概率比接近1，说明新旧策略对这个动作的偏好差不多。
- 如果概率比远大于1，说明新策略更偏好这个动作。
剪裁操作：强制概率比在区间 [1-ε, 1+ε]（比如ε=0.2）。相当于说：
- 如果某个动作特别好，最多让它的概率比旧策略高20%；如果特别差，最多低20%。
- 避免某个动作的概率被无限放大或缩小，保持更新稳定。

4. 数据复用：重要性采样

问题：传统方法每更新一次策略，就要重新试错，效率低。
解决方案：用旧策略收集的数据训练新策略，但通过重要性权重（即概率比）修正数据分布差异。
- 例如：旧策略有10%概率跳高，新策略变成20%，则跳高动作的权重为2（20%/10%）。
- 但PPO2会通过剪裁限制权重在[0.8, 1.2]之间，避免某个动作的权重过大导致训练不稳定。

5. Actor-Critic 搭档

PPO通常结合两种网络：

Actor（演员）：负责选择动作（狗的跳高策略）。
Critic（评论家）：评估当前状态的价值（比如：当前位置接飞盘的潜力有多大）。
- Critic的作用是提供更精细的反馈，帮助Actor判断哪些动作长期来看更好，而不仅仅是看单次奖励。

6. PPO的优势总结

稳定训练：限制策略更新幅度，避免“一步错步步错”。
高效复用数据：通过重要性采样，旧数据也能多次利用。
通用性强：适用于连续动作（如机器人控制）和离散动作（如游戏AI）。

举个栗子 🌰

假设狗当前策略是“看到飞盘跳50cm高”，PPO的更新过程如下：

收集数据：用当前策略试跳10次，记录哪些动作成功接到飞盘。
评估优势：Critic会分析，跳55cm可能比50cm更好（比如飞盘飞得更高时）。
限制更新：允许新策略调整为“跳55cm”，但不允许突然改成“跳100cm”（概率比剪裁在0.8~1.2之间）。
重复优化：用新策略继续试跳，逐步逼近最佳高度。

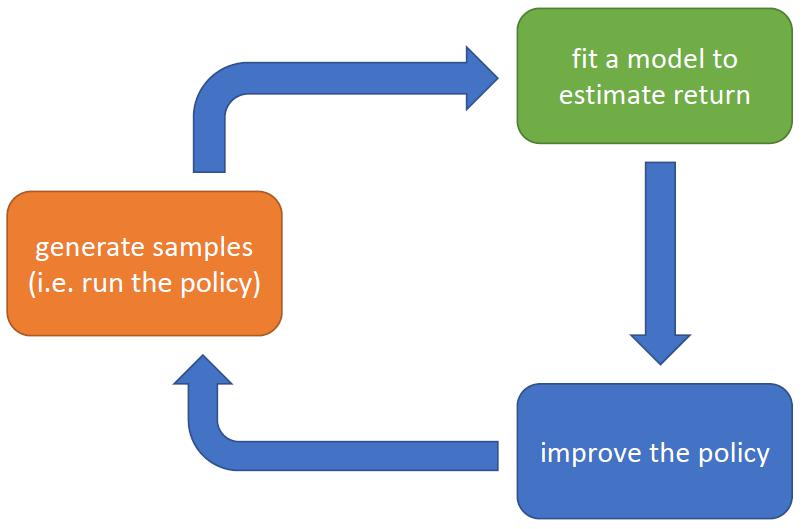
一句话理解PPO

“小步改进旧策略，数据复用不浪费，剪裁限制别作死，ActorCritic好搭配。”

公式

1. 目标函数与期望奖励

公式：
$\theta^{*} = \arg\max_{\theta} E_{\tau \sim \pi_{\theta}(\tau)} [\sum_{t} r(s_t, a_t)]$
解释：
目标是找到参数 θ，使得从策略采样的轨迹的期望总奖励最大。由于策略和环境具有随机性，需通过期望值评估平均性能。
$\theta^{*}$ ：是我们要寻找的最优策略参数。它能使策略 $\pi_{\theta}$ （由参数 $\theta$ 决定的策略）获得最大的期望总奖励。

$\arg\max_{\theta}$ ：这是一个求使函数取最大值时参数值的操作符。意思是在所有可能的参数 $\theta$ 中，找到能让后面期望项最大的那个 $\theta$ 。

$E_{\tau \sim \pi_{\theta}(\tau)}$ ：表示对从策略 $\pi_{\theta}$ 采样得到的轨迹 $\tau$ 求期望。由于策略和环境都有随机性，每次采样得到的轨迹不同，通过求期望来评估策略的平均性能。

$[\sum_{t} r(s_t, a_t)]$ ：是沿着轨迹 $\tau$ ，对每个时间步 t 的即时奖励 $r(s_t, a_t)$ 进行求和，得到一条轨迹的总奖励。

通过蒙特卡洛采样近似计算 $J(\theta) \approx \frac{1}{N} \sum_{i = 1}^{N} \sum_{t = 1}^{T} r(s_{i,t}, a_{i,t})$

因为直接求期望比较困难，所以采用蒙特卡洛采样来近似。

N 是采样的轨迹数，通过多次采样不同轨迹来近似期望。

T 是单条轨迹的步数。对每条轨迹上每个时间步的奖励求和，再对 N 条轨迹的奖励和求平均，以此来近似期望奖励 $J(\theta)$ 。

2. 策略梯度推导

公式：

$\nabla J(\theta) = E_{\tau \sim \pi_{\theta}(\tau)} [(\sum_{t = 1}^{T} \nabla \log \pi_{\theta}(a_t | s_t)) (\sum_{t = 1}^{T} r(s_t, a_t))]$

$\nabla J(\theta)$ ：是目标函数 $J(\theta)$ 关于参数 $\theta$ 的梯度。它指示了参数 $\theta$ 朝哪个方向更新能使目标函数增大。

$E_{\tau \sim \pi_{\theta}(\tau)}$ ：同样是对从策略 $\pi_{\theta}$ 采样得到的轨迹 $\tau$ 求期望。

$(\sum_{t = 1}^{T} \nabla \log \pi_{\theta}(a_t | s_t))$ ：对每个时间步上动作概率的对数求梯度并累加。利用对数概率技巧 $\nabla \pi_{\theta} = \pi_{\theta} \nabla \log \pi_{\theta}$ 转换而来，这样便于计算和分析策略的变化。

$(\sum_{t = 1}^{T} r(s_t, a_t))$ ：一条轨迹上的总奖励，它作为权重，表明哪些时间步上策略的变化对总奖励影响大，就更值得去调整。

推导关键步骤：

对数概率技巧： $\nabla \pi_{\theta} = \pi_{\theta} \nabla \log \pi_{\theta}$ ，将对策略 $\pi_{\theta}$ 本身求梯度转换为对其对数求梯度，在数学计算和分析上更方便，因为对数函数的导数形式相对简单，便于后续处理。

梯度转换为期望形式：把策略梯度表示为对轨迹求期望的形式，这样符合策略在随机环境下的特性，从概率角度来描述策略变化对奖励的影响。

分解轨迹概率： $\pi_{\theta}(\tau) = p(s_1) \prod_{t = 1}^{T} \pi_{\theta}(a_t | s_t) p(s_{t + 1} | s_t, a_t)$ ，将轨迹的概率分解为起始状态概率、每个时间步动作概率和状态转移概率的乘积。

取对数后 $\log \pi_{\theta}(\tau) = \sum_{t = 1}^{T} \log \pi_{\theta}(a_t | s_t) + \text{number}$ ，方便计算关于动作概率的梯度，因为常数项number求导为0 ，最终梯度就只依赖动作概率的梯度加权求和。

3. 基线（Baseline）减方差

公式：

$\nabla J(\theta) \approx \frac{1}{N} \sum_{i = 1}^{N} (\sum_{t = 1}^{T} \nabla \log \pi_{\theta}(a_{i,t} | s_{i,t})) (R(\tau_i) - b)$
解释：

$R(\tau_i)$ ：表示第 i 条轨迹的总奖励。

$b = \frac{1}{N} \sum_{i = 1}^{N} R(\tau_i)$ ：是所有 N 条轨迹的平均奖励，作为基线。

从梯度计算公式中减去基线 b ，目的是保留动作相对于平均水平的优势。比如某个动作带来的奖励高于平均奖励， $(R(\tau_i) - b)$ 为正，会促使策略往增加该动作概率的方向更新；反之则促使减少概率。同时，这种方式能降低梯度估计的方差，使训练过程更稳定，因为减去基线后，减少了奖励波动对梯度估计的影响。

4. On-policy 与 Off-policy

On-policy：含义是使用当前正在优化的策略 $\pi$ 与环境进行交互，产生的数据仅用于一次策略更新。比如在训练一个智能体玩游戏时，智能体按照当前策略去玩游戏，收集到的游戏过程数据只用来更新这一次策略，下次更新策略时需要重新用当前策略去和环境交互收集新数据。这种方式的优点是策略更新直接基于当前策略产生的数据，比较 “纯粹” ，但缺点是数据利用率低，每次更新都需要重新收集数据，训练效率不高。
Off-policy：使用一个旧策略 $\pi_{old}$ 来生成数据，然后通过重要性采样技术对这些数据进行处理，以便能够重复利用这些数据来更新当前要优化的策略。重要性采样公式 $E_{x \sim p}[f(x)] = E_{x \sim Q}[\frac{p(x)}{Q(x)}f(x)]$ 这里 p(x) 是目标分布（当前策略对应的分布）， Q(x) 是行为分布（旧策略对应的分布）。在策略梯度中的应用公式 $\nabla_{\theta} J(\theta) = E_{\tau \sim \pi} [\frac{\pi(\tau)}{\pi_{old}(\tau)} \nabla_{\theta} \log \pi(\tau) r(\tau)]$ 通过计算新旧策略下轨迹的概率比值，来修正旧策略数据用于更新当前策略时的偏差，从而实现数据的重复利用，提高训练效率。

重要性采样公式：
$E_{x \sim p}[f(x)] = E_{x \sim Q}[\frac{p(x)}{Q(x)}f(x)]$
应用到策略梯度：

$\nabla_{\theta} J(\theta) = E_{\tau \sim \pi} [\frac{\pi(\tau)}{\pi_{old}(\tau)} \nabla_{\theta} \log \pi(\tau) r(\tau)]$

5. KL 散度约束与 PPO2 剪裁

目标函数约束：
在近端策略优化中，为了防止策略更新幅度过大导致训练不稳定，引入了新旧策略的KL散度约束。KL散度用于衡量两个概率分布（这里是新旧策略对应的动作概率分布）之间的差异。要求新旧策略的KL散度小于阈值 $\epsilon$ ，如果更新后的策略与旧策略差异过大，可能会使智能体的行为突然改变，导致性能下降甚至训练失败。
PPO2 目标函数：
$J_{PPO2}^{\theta}(\theta)=\sum_{(s_t,a_t)} \min(\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}A^{\theta}(s_t,a_t), clip(\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)},1 - \epsilon,1 + \epsilon)A^{\theta}(s_t,a_t))$
解释：

优势函数 $A^{\theta}$ ：由Critic网络评估得到，它表示在状态 $s_t$ 下采取动作 $a_t$ 相对于基线（比如状态价值 $V(s_t)$ ）的优势程度。如果优势函数值为正，说明该动作相对较好；为负则相对较
剪裁操作：限制重要性权重在 [1−ϵ,1+ϵ] 之间，避免因概率比过大导致梯度爆炸。

6. Actor-Critic 架构

Actor（策略网络）：输出动作概率 $\pi_{\theta}(a_t|s_t)$ ，通过梯度上升更新。
Critic（价值网络）：估计状态价值 $V(s_t)$ ，作为基线或计算优势函数：
$A(s_t,a_t)=Q(s_t,a_t)-V(s_t)$ .
作用：Critic 提供更稳定的评估，帮助 Actor 区分高/低质量动作。

7. PPO 算法流程

数据收集：使用当前策略 πθk 与环境交互，生成轨迹数据集。
优势估计：Critic 网络计算每个 $s_t,a_t$ 的优势值 $A^{\theta}(s_t,a_t)$ 。
目标函数优化：通过随机梯度上升最大化 PPO2 目标函数，更新策略参数 θ。
迭代更新：重复上述步骤，直到策略收敛。

关键公式总结

概念	公式
目标函数	$\theta^{*} = \arg\max_{\theta} E_{\tau \sim \pi_{\theta}(\tau)} [\sum_{t} r_t]$
策略梯度	$\nabla_{\theta} J(\theta) = E_{\tau} [(\sum_{t} \nabla \log \pi_{\theta}(a_t \| s_t)) (\sum_{t} r_t)]$
基线减方差	$\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i = 1}^{N} (\sum_{t = 1}^{T} \nabla \log \pi_{\theta}(a_{i,t} \| s_{i,t})) (R(\tau_i) - b)$
重要性采样	$E_{x \sim P}[f(x)] = E_{x \sim Q}[\frac{P(x)}{Q(x)}f(x)]$
PPO2 目标函数	$J_{PPO2} = \sum_{(s_t,a_t)} \min(\text{ratio} \cdot A, \text{clip}(\text{ratio}) \cdot A)$