【机器学习】线性回归概念及应用

一、一元线性回归

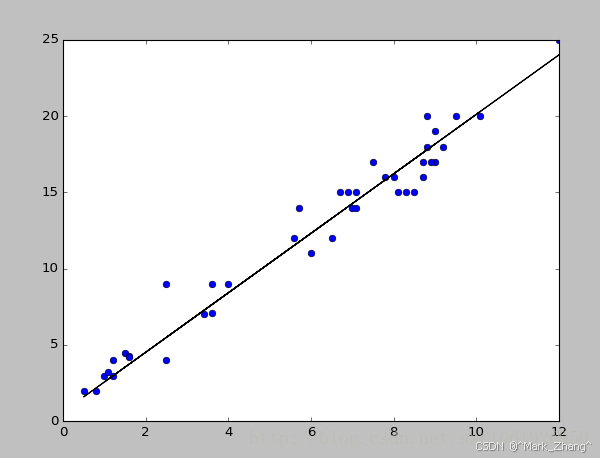
1.1 算法原理

目的：仅仅通过一个变量预测因变量
举个例子：仅仅通过发量判断程序员水平
此时表示函数：

y = $\omega$x + b

1.2 线性回归中的估计

1.2.1 最小二乘估计

目的：基于军方误差最小化来进行模型求解的方法：
对于函数 y = $\omega$x + b ,我们定义如下公式求解误差：

$\begin{array}{rl}{E}_{(w,b)}& =\sum _{i=1}^m{\left(y_i-f(x_i)\right)}^2\\ & =\sum _{i=1}^m{\left(y_i-(w{x}_i+b)\right)}^2\\ & =\sum _{i=1}^m{\left(y_i-w{x}_i-b\right)}^2\end{array}$

从几何角度理解就是当前数据点的y坐标值跟用于拟合的函数上同横坐标对应的纵坐标的差值的平方。

1.2.2 极大似然估计

目的：用于估计概率分布的参数值，个人感觉有点像生物学中的抽样调查。
举个例子：要调查学校中的雌性生物和雄性生物的比例，并不是将所有生物都捉起来，而是抽取其中的一部分进行统计。
公式如下：

$L(\theta )={\prod }_{i=1}^{n}P(x_i;\theta )$

其中$\theta$是未知数，这个概率是关于$\theta$的函数，称L($\theta$)为样本的似然函数。使得函数取到最大值的${\theta }^{\ast }$就是$\theta$的估计值。

1.3 求解 $\omega$ 和 b

大家都知道机器学习问题主要解决的就是优化问题，由此衍生出来的数学理论目的也是求解优化问题。

先验知识

凸集：集合$D\subset {\mathbb{R}}^n$,如果对任意的$x,\mathbf{y}\in D$与任意的$\alpha \in [0,1]$, 有$$\alpha \mathbf{x}+(1-\alpha )\mathbf{y}\in D$$
梯度：梯度 (多元函数的一阶导数) : 设n元函数$f(\mathbf{x})$对自变量$\mathbf{x}=(x_1,x_2,...,x_n{)}^{\mathrm{T}}$的各分量$x_i$的偏导数$\frac{\partial f(x)}{\partial x_i}(i=1,...,n)$都存在，则称函数$f(\mathbf{x})$在$x$处一阶可导，并称向量$\nabla f(\mathbf{x})=[\begin{array}{c}\frac{\partial f(\mathbf{x})}{\partial x_1}\\ \frac{\partial f(\mathbf{x})}{\partial x_2}\\ ⋮\\ \frac{\partial f(\mathbf{x})}{\partial x_n}\end{array}]$ 为函数$f(\mathbf{x})$在$\mathbf{x}$处的一阶导数或梯度。
这里我们一般就使用列矩阵（分母型）

求解

凸充分性定理：若$\dot{f}:{\mathbb{R}}^n\to \mathbb{R}$是凸函数，且$f(\mathbf{x})$一阶连续可微，则$x^{\ast }$是全局解的充分必要条件是$\nabla f(x^{\ast })=0$

所以，$\nabla E_{(w,b)}=0$的点即为最小值点，也即$\nabla E_{(w,b)}=[\begin{array}{c}\frac{\partial E(w,b)}{\partial w}\\ \frac{\partial E(w,b)}{\partial b}\end{array}]=\left[\begin{array}{c}0\\ 0\end{array}\right]$

先对$b$进行求导和化简：

$\begin{array}{c}\frac{\partial E_{(w,b)}}{\partial b}=2\left(mb-\sum _{i=1}^m\left(y_i-w{x}_i\right)\right)=0\\ mb-\sum _{i=1}^m(y_i-w{x}_i)=0\\ b=\frac{1}{m}\sum _{i=1}^m(y_i-w{x}_i)\\ b=\frac{1}{m}\sum _{i=1}^m{y}_i-w\cdot \frac{1}{m}\sum _{i=1}^m{x}_i=\bar{y}-w\bar{x}\end{array}$

把$b=\bar{y}-w\bar{x}$代入上式可得:

$\begin{array}{c}w\sum _{i=1}^m{x}_i^2=\sum _{i=1}^m{y}_i{x}_i-\sum _{i=1}^m(\bar{y}-w\bar{x})x_i\end{array}$

进一步推导可以得到：

$w=\frac{{\sum }_{i=1}^m{y}_i{x}_i-\bar{x}{\sum }_{i=1}^m{y}_i}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{mt}}=\frac{{\sum }_{i=1}^m{y}_i(x_i-\bar{x})}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{mt}\frac{1}{{\sum }_{i=1}^m{x}_i{)}^2}({\sum }_{i=1}^m{x}_i{)}^2}$

二、多元线性回归

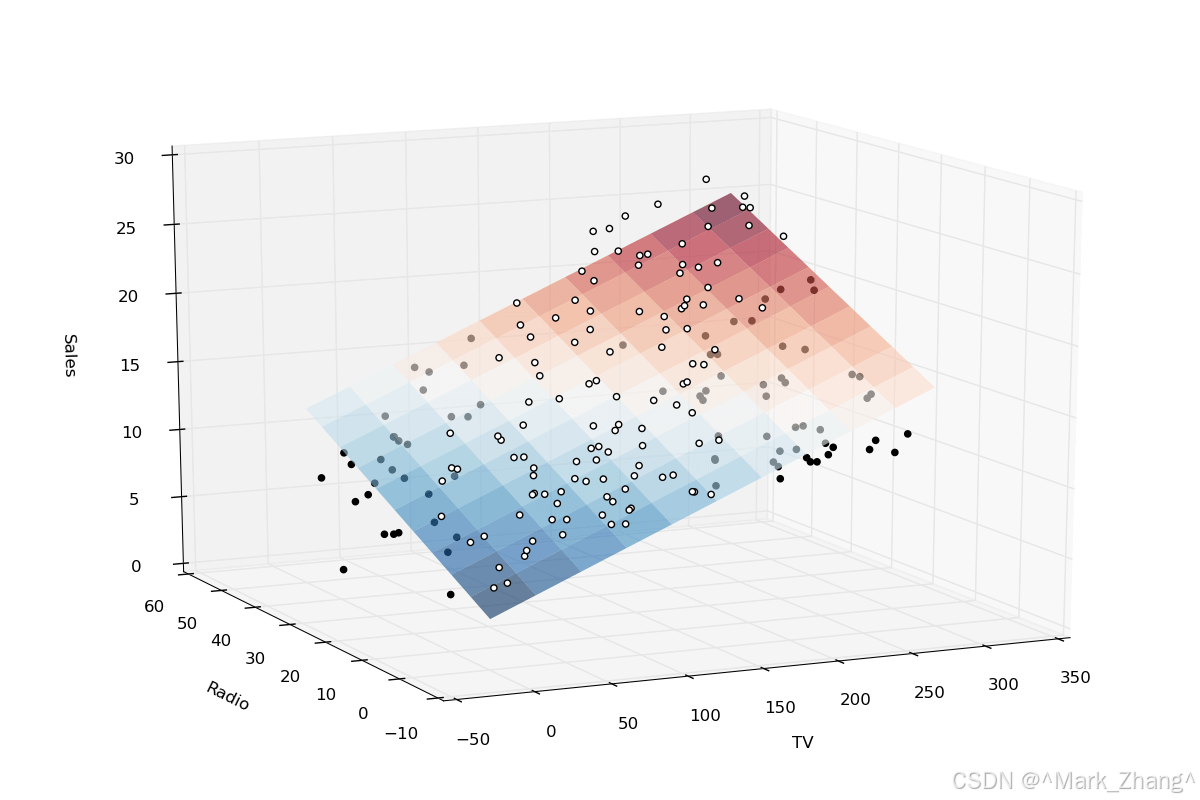
2.1 算法原理

在一元线性回归的基础上加了多值离散特征
举个栗子：在前面的通过发亮判断程序员水平的基础上增加了其他变量，比如增加了颜值（好、差）、代码量项目经历（少、中、多）等。
此时原来的函数变成了：

y = ${\omega }_1$x1 + ${\omega }_2$x2 + ${\omega }_3$x3 + ${\omega }_4$x4 + ${\omega }_5$x5 + ${\omega }_6$x6 + b

2.2 公式推导

对于多元变量，我们为了能够用numpy库进行运算加速，采用向量表达的方式。

$f({\mathbf{x}}_i)={\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b$

也就是：

$f\left({\mathbf{x}}_i\right)=w_1{x}_{i1}+w_2{x}_{i2}+...+w_d{x}_{id}+w_{d+1}\cdot 1$

$\begin{array}{rl}\text{由最小二乘法可得}& \\ E_{\hat{\mathbf{w}}}& =\sum _{i=1}^m(y_i+f({\hat{\mathbf{x}}}_i){)}^2=\sum _{i=1}^m{\left(y_i-{\hat{\mathbf{w}}}^{\mathrm{T}}{\hat{\mathbf{x}}}_i\right)}^2\end{array}$

接下来就是求解${\hat{\omega }}^{\ast }$使得这个函数取最值。（证明过程略，本人太菜暂时还没懂>_<）