【西瓜书Chapter2】线性回归

m0_49223946

于 2022-10-17 21:04:00 发布

阅读量355

点赞数

文章标签：算法

本文链接：https://blog.csdn.net/m0_49223946/article/details/127358211

版权

线性回归

给定由d个属性描述的示例 $\vec{x}=(x_{1};x_{2};\cdots ;x_{d})$ ，其中 $x_{i}$ 是 $\vec{x}$ 在第 $i$ 个属性上的取值，线性模型（linear model）试图学得一个通过属性的线性组合来进行预测的函数，即

$\mathbf{\mathit{f}(x)}=w_{1}x_{1}+w_{2}x_{2}+\cdots +w_{d}x_{d}+b$

一般用向量形式写成

$\mathbf{\mathit{f}(x)}=\mathbf{w}^{T}\mathbf{x}+b$

其中 $\vec{x}$ 为已知输入特征向量， $\mathbf{w}$ 和 $b$ 学得之后，模型就可以确定。

一元线性回归算法原理

给定数据集 $D=\left \{ (\mathbf{x}_{1},{y}_{1}),(\mathbf{x}_{2},{y}_{2}),\cdots ,(\mathbf{x}_{m},{y}_{m}) \right \}$ ，其中 $\mathbf{x}_{i}=(x_{i1};x_{i2};\cdots ;x_{id})$ ， $y_{i}\in \mathbb{R}$ 。"线性回归“试图学得一个线性模型以尽可能准确地预测实值输出标记。

我们先考虑一种最简单的情形：输入属性的数目只有一个。为便于讨论此时我们忽略关于属性的下标，即 $D=\left \{ (x_{i},y_{i}) \right \}_{i=1}^{m}$ ，其中 $x_{i}\in \mathbb{R}$ 。

举一个通过【发际线高度】预测【计算机水平】的例子。

$f(x_{i})=wx_{i}+b,\; x_{i}=1,2,\cdots m$

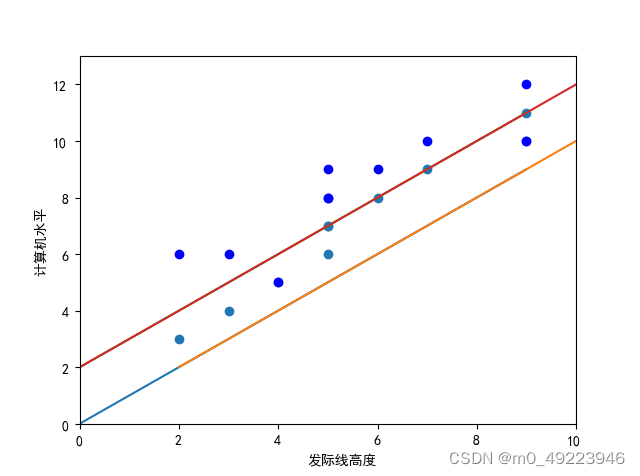
如何确定w和b呢？显然，关键在于如何衡量 $f(x)$ 与 $y$ 之间的差别。

画出样本点的分布图后，我们要找出所有样本点到最终模型最近的一条直线，这里我们用样本值减去预测值得到预测误差，在求平方获得正误差。基于均方误差最小化来进行模型求解的方法称为最小二乘法：

$E(w,b)=\sum_{i=1}^{m}(y_{i}-f(x_{i}))^{2}$

均方误差是回归任务中最常用的性能度量，因此我们可试图让均方误差最小化，即

$(w^*,b^*)=\underset{(w,b)}{arg\; min}\sum_{i=1}^{m}(f(x_i)-y_i)^2=\underset{(w,b)}{arg\; min}\sum_{i=1}^{m}(y_i-wx_i-b)^2$

确定了 $w$ 和 $b$ 的最小值便确定了模型。

多元线性回归算法原理

还是这个例子，现在我们加入另外几个影响发际线高度的特征。

仅通过【发际线高度】预测【计算机水平】：

$f(x)=w_{1}x_{1}+b$

+二值离散特征【颜值】（好看：1，不好看：0）

$f(\vec{x})=w_{1}x_{1}+w_{2}x_{2}+b$

+有序的多值离散特征【饭量】（小：1，中：2，大：3）

$f(\vec{x})=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+b$

+无序的多值离散特征【肤色】（黄：[1, 0, 0]，黑：[0, 1, 0]，白：[0, 0, 1]）

$f(\vec{x})=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+w_{4}x_{4}+w_{5}x_{5}+w_{6}x_{6}+b$

此时我们试图学得

$f(\mathbf{x}_{i})=\mathbf{w}^{T}\mathbf{x}_{i}+b$

这称为多元线性回归（multivariate linear regression）。

为了便于讨论，我们把 $\mathbf{w}$ 和 $b$ 吸收入向量形式 $\hat{w}=(\mathbf{w};b)$ ，把 $b$ 扩充到 $\mathbf{w}$ 中，

$f(\mathbf{x_{i}})=\begin{pmatrix} w_{1} &w_{2} &\cdots &w_{d} \end{pmatrix} \begin{pmatrix} x_{i1}\\ x_{i2}\\ \vdots \\ x_{id} \end{pmatrix} +b$

$f(\mathbf{x}_i)=w_1x_{i1}+w_2x_{i2}+\cdots +w_dx_{id}+b$

$f(\mathbf{x}_i)=w_1x_{i1}+w_2x_{i2}+\cdots +w_dx_{id}+w_{d+1}\cdot 1$

令 $\mathbf{\hat{x}}_i=(\mathbf{x}_i;1)$ ，则

$f(\mathbf{\hat{x}}_i)=\mathbf{\hat{w}}^{T}\mathbf{\hat{x}}_i$

由最小二乘法可得

$E\mathbf{\hat{w}}=\sum_{i=1}^{m}(y_i-f(\mathbf{\hat{x}}_i))^{2}=\sum_{i=1}^{m}(y_i-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_i)^2$

接下来对上式进行向量化，便于使用numpy等矩阵加速库加速计算。

$E\mathbf{\hat{w}}=\sum_{i=1}^{m}(y_i-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_i)^2=(y_1-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_1)^2+(y_2-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_2)^2+\cdots +(y_m-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_m)^2$

$E\mathbf{\hat{w}}= \begin{pmatrix} y_1-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_1& y_2-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_2 & \cdots & y_m-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_m \end{pmatrix} \begin{pmatrix} y_1-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_1\\ y_2-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_2\\ \vdots \\ y_m-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_m \end{pmatrix}$

把数据集D表示为一个 $m\times (d+1)$ 大小的矩阵 $\mathbf{X}$ ，

$X=\begin{pmatrix} &x_{11} &x_{12} &\cdots &x_{1d} &1\\ &x_{21} &x_{22} &\cdots &x_{2d} &1\\ &\vdots &\vdots &\ddots &\vdots &\vdots \\ &x_{m1} &x_{m2} &\cdots &x_{md} &1 \end{pmatrix}=\begin{pmatrix} &\mathbf{x}_{1}^{T} &1 \\ &\mathbf{x}_{2}^{T} &1 \\ &\vdots &\vdots \\ &\mathbf{x}_{m}^{T} &1 \end{pmatrix}$

则

$\begin{pmatrix} y_1-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_1\\ y_2-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_2\\ \vdots\\ y_m-\mathbf{\hat{w}}^T\mathbf{\hat{x}}_m \end{pmatrix} = \begin{pmatrix} y_1\\ y_2\\ \vdots\\ y_m \end{pmatrix} - \begin{pmatrix} \mathbf{\hat{w}}^T\mathbf{\hat{x}}_1\\ \mathbf{\hat{w}}^T\mathbf{\hat{x}}_2\\ \vdots\\ \mathbf{\hat{w}}^T\mathbf{\hat{x}}_m \end{pmatrix} = \begin{pmatrix} \mathbf{\hat{x}}_1^T\mathbf{\hat{w}}\\ \mathbf{\hat{x}}_2^T\mathbf{\hat{w}}\\ \vdots\\ \mathbf{\hat{x}}_m^T\mathbf{\hat{w}} \end{pmatrix}$

$\begin{pmatrix} \mathbf{\hat{x}}_1^T\mathbf{\hat{w}}\\ \mathbf{\hat{x}}_2^T\mathbf{\hat{w}}\\ \vdots\\ \mathbf{\hat{x}}_m^T\mathbf{\hat{w}} \end{pmatrix} = \begin{pmatrix} \mathbf{\hat{x}}_1^T\\ \mathbf{\hat{x}}_2^T\\ \vdots\\ \mathbf{\hat{x}}_m^T \end{pmatrix} \cdot \mathbf{\hat{w}} =\mathbf{X}\cdot\mathbf{\hat{w}}$