那些你不理解的dp背包问题的详解

Victory_orsh

已于 2024-02-15 11:12:13 修改

阅读量970

点赞数 19

分类专栏：通俗易懂寒假正在学…… 文章标签： c++ 算法动态规划

于 2024-02-08 17:16:36 首次发布

本文链接：https://blog.csdn.net/weixin_73074505/article/details/135965578

版权

寒假正在学…… 同时被 2 个专栏收录

12 篇文章 0 订阅

订阅专栏

通俗易懂

11 篇文章 0 订阅

订阅专栏

一、声明

本文旨在以最通俗易懂的语言讲解动态规划中背包问题的细节问题，这些问题可能成为理解动态规划中的一个个小障碍，这篇文章就是对这类问题的总结归纳，争取实现让读者初步了解dp后可以通过这篇文章查询到每个疑问，而不是一个个查询消耗热情。

在阅读时，可以直接根据目录跳转到你的问题，也可以通读全文，或学习或梳理dp脉络。

欢迎提问、补充、质疑。

（1）为什么直接是f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i])？

（2）为什么可以优化成二重循环？（原理）

（3）与01背包一维优化的比较

（4）为什么第二层循环要从小到大？

3.有个数限制的背包问题（多重背包与分组背包）

二、回顾dp

这里首先给出y总的思维图帮助回忆dp做题流程：

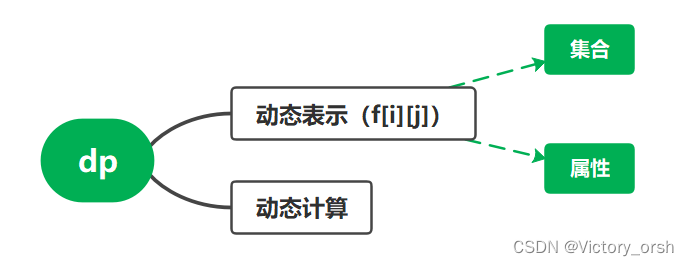
其实很简单，就是你要搞清 $f[i][j]$ 代表的是什么，打个比方：前i件物品中选且体积不超过j的最大价值。或者说，搞清i是什么，j是什么， $f[i][j]$ 的值是什么，加粗部分就是答案。

还有呢，就是如何计算，也就是找出状态之间的关系来求最优解，打个比方： $f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i])$ ，这就是01背包问题的状态计算方程，在这里不过多阐述，下文以模拟的形式来直观理解。

本文模拟

现在直接开始模拟，模拟是我们最能感受到算法实质的方法，也可以直接消除我们很多疑惑。

直接从最基本的问题出发，看看它究竟是怎么运行的，就像是你想知道自行车为什么比人走着快，然后自己一边观察一边跑，发现了原来是杠杆原理：蹬一轮大圈，小圈转好几轮，轮胎也就多转好几圈。虽然可能有些累，但既锻炼了身体，又拥有了造自行车的能力。

不必模拟太多，此例仅给出三个物品进行01背包操作（图中左侧），右侧则是dp矩阵（ $f[i][j]$ 的状态）。

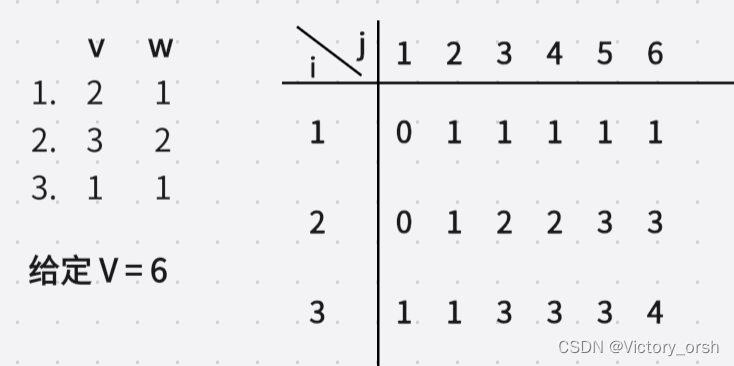
如果不知道如何得出：根据此式： $f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i])$ ，举个例子：当i == 2，j == 3时（前2个物品中选且体积不超3的最优情况），选第2个物品还是不选呢？不选：直接是 $f[1][3]$ = 1；选： $f[1][0]+w[2]$ = 2，2 > 1，所以选。

动态规划的过程实际上就是生成一个全局矩阵的过程，和贪心的区别也就在此，你不能仅仅根据当前最优就一步步得到整体最优，而需要考虑全局，根据之前的最优态推出当前。

三、具体细节问题

1.一维优化问题（01）

（1）为什么要进行优化？

dp矩阵空间占用较大，最低为N*V，可能MLE，所以能优化尽量优化。

（2）如何一维优化？

优化前： $f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i])$

优化后： $f[j] = max(f[j],f[j-v[i]]+w[i])$

（3）为什么可以一维优化？

也就是解释（2）中优化后的式子。

为什么可以直接将矩阵中的横坐标（这样说不规范但易理解）去掉呢？那肯定是没用了啊。我们每次都只用得到当前层i（用于更新储存）和上一层i-1（用于计算）【这里可以参照二中的本文模拟的图或者下面的图】，不信你看二维公式。那不是用到i-1层了吗，怎么就一维？因为在这一层循环访问f[j]的时候留下来的是上一层循环的数值啊！这就是短暂的记忆，也就是滑动数组。

（4）为什么第二层循环要从大到小？

先给出最终优化代码：

for(int i=1;i<=n;i++){
        for(int j=m;j>=v[i];j--)
                f[j]=max(f[j],f[j-v[i]]+w[i]);

话不多说，模拟：

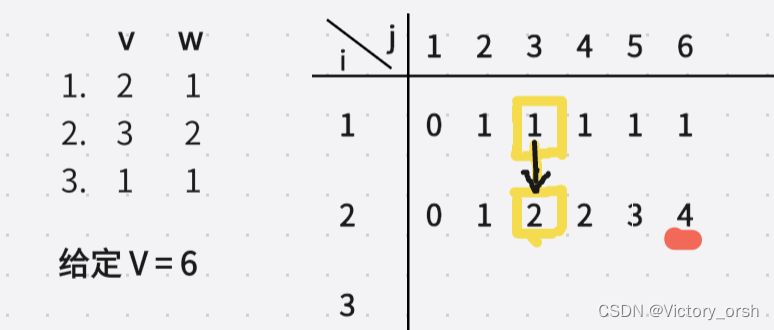
翻回上一个图对比一下，是不是红色标出的数冲突了，至于为什么，还是希望大家亲自动手模拟一下，解释：因为图中是从小到大模拟的，这样就会导致在i == 2，j == 6时，我本来希望得到i-1层的f[3]（f[6-v[2]]得到），然后加上w[2]来和不选的f[1][6]比较，但是f[3]已经被覆盖更新了，意味着在j == 3时已经被拿过一次了，如果继续用当前的f[3]，相当于拿了两次，所以结果错误，拿了两次物品1。

自然，从大到小可以完美避免这种问题，用到的都是之前的（比当前j小的），都没被覆盖。其实就一句话：从小到大，我想用的，已经被覆盖（用过）了。

2.完全背包优化问题

（0）完全背包简述

优化前：

for(int i=1;i<=n;i++)
    for(int j=0;j<=v;j++)
        for(int k=0;k*v[i]<=j;k++)
            f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);

也就是本来只能拿一个，那就是拿还是不拿比较，现在可以拿无限个，那就无限个相比较呗，哈哈，当然不行，你得小于当前体积限制 j 啊，这就有了第三层循环。

（1）为什么直接是f[i][j] = max(f[i][j],f[i-1][j-kv[i]]+kw[i])？

一句话：k+1种情况的比较

想一想，就是选0个、选1个……到选k个，注意到：k是从0开始的。是不是很多同学不理解这个问题是因为不明白为什么 f[i][j] 可以和 f[i][j] 相比较，它不是没有被更新过吗？再怎么样也得在前面加上 f[i][j] = f[i-1][j] 啊，也就是为什么不是f[i][j] = max(f[i-1][j],f[i-1][j-k*v[i]]+k*w[i])。

其实不然，实际上第一次k=0的循环就是 f[i][j] = f[i-1][j] 的操作，因为第一次f[i][j]没更新为0，而k又为0，那肯定就是上一层的值了。那是不是可以加上这个式子呢？答案是不可以！因为这不是01背包，每次就是选还是不选比，这里有无限个物品，如果加上，那每次都是：不选与选k个物品相比。很明显，这是不对的。应该是每次将最大值存给 f[i][j]，再与下一个情况相比。

（2）为什么可以优化成二重循环？（原理）

我们根据二中的做题流程可以推出（不管j是多少，都是拿几个(1-k)当前物品相比较）：

f[i,j] = max( f[i-1,j] , f[i-1,j-v]+w ,  f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....)
f[i，j-v] = max(            f[i-1,j-v]   ,  f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , .....)

仔细观察，发现二者除却第一项就只差个w，那怎么办？当然是代换啦。

这样就成了不拿(f[i-1,j])和拿(f[i,j-v]+w)的比较，也就自然地省去了第三个循环，其实是被包含在拿里，就换成了：

for(int i=1;i<=n;i++)
    for(int j=0;j<=v;j++){
        f[i][j]=f[i-1][j];
        if(j>=v[i])
            f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);
        }

（3）与01背包一维优化的比较

在前面，我们将完全背包化成了二重循环，那接下来就是进一步将其优化成与01背包类似的一维形式了，那该如何优化呢？

这里，我们参考01背包的示例，同样考虑在选取当前物品时是不是可以省略离得较远的状态，也就是只考虑近期状态实现一维。答案是可以的。

观察完全背包核心公式： $f[i][j] = max(f[i-1][j],f[i][j-v[i]]+w[i])$

再观察01背包核心公式： $f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i])$

可看出只一个i与i-1之差，第一个i-1不用管，因为化成一维都是值上一层的 $f[i-1][j]$ 。主要看第二个：01背包用上一层，完全背包用当前一层。都用不到之前的状态，可化一维。

注意：首先，如果你看过（1），不要疑惑完全背包公式为什么又是i-1了，这里已经去除循环了，仔细再看一遍（1）。

第二，许多资料将这两个公式中第一个i-1都替换成i，实际是一样的，因为前面都会加一个 $f[i][j]=f[i-1][j]$ ，但是i-1更能体现出其本质。

（4）为什么第二层循环要从小到大？

先给出最终优化代码：

for(int i = 1 ; i<=n ;i++)
        for(int j = v[i] ; j<=m ;j++)
            f[j] = max(f[j],f[j-v[i]]+w[i]);

我们会发现，完全背包优化后的 j 循环怎么与01背包简化后的 j 循环不同？

对于01背包，我们知道每次更新数据用到的都是记忆化存下的第 i-1层的数据，因此逆序可以保证更新 j 时，j 前面的数据都没有被覆盖；而对于完全背包，我们用到的都是当前第 i 层的数据，只有从小到大更新才能有的用啊。那你会不会问：那第一个是怎么来的呢？看代码，第一个一定是f[0]，一定为0。那自然地，它也是绝不能反过来，不然用的就是上一层数据了。

3.有个数限制的背包问题（多重背包与分组背包）

（0）简述

如果对前面的一维优化与完全背包优化有了比较清晰的认识，这类问题其实就迎刃而解了，所以我将这两个一起来说，当作两个变式。都可以用二中的方法进行分析，最后会有综合讲述。

（1）多重背包简述

题意：多重背包就是完全背包加上了个数限制，现在对于每一个物品最多取 s[i] 个，而不是无限个。

思路：回想完全背包，我们实际上就是遍历了每一种情况，将其分成了01背包，看看每一个物品要不要选，当然我们需要加上限制条件：件数k*v[i]不能大于当前体积 j ，而多重背包亦可如此，反而更简单了，因为限制条件已经给出：件数不能大于 s[i] 。

代码：

for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
        for(int k=0;k<=s[i];k++)
            if(j>=k*v[i])
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+w[i]*k);

与2中（0）对比，清晰明了。

（2）二进制优化

多重背包最重要的是二进制优化。

背景：如果不进行优化，时间复杂度： $N*s_{i}*M$ 优化后： $N*log_{2}s_{i}*M$

而二进制优化在背包问题上的应用一定是在同种物品上使用。

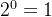
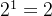
内容：对于任何一个数n，由0到n都可以由和不大于它的二进制数字及剩余数字组成。举例：对于20，和不大于它的二进制数字有 $2^{0}=1$ $2^{1}=2$ $2^{2}=4$ $2^{3}=8$ ，相加得15嘛，再加一个 $2^{4}=16$ 就大于20了。那什么叫剩余数字：剩余数字就是20减去前面二进制数字的和，即20-15 = 5 。所以，0到20中的任一数字都可以由1、2、4、8、5，实践出真知，自己随便举个数试一试就明白了。

原理：前面的二进制数字可以构成0到m（ $m=\sum_{k=0}^{k}2^{k}$ , $m\leqslant n$ , $\sum_{k=0}^{k+1}2^{k}>n$ ）,而加上剩余数字n-m，可构成数字范围就变成了0到n，符合要求。

思路：回归题目，这样一来，原本我们一个一个物品来看就变成了一堆一堆物品来看，将具有相同体积价值的物品进行二进制打包成堆。

代码：注释很详细

int cnt = 0; //总共有几堆
    for(int i = 1;i <= n;i ++)
    {
        int a,b,s;
        cin >> a >> b >> s;
        int k = 1; // 当前种类下当前堆中的物品个数
        while(k<=s)// s的代表总个数减去二进制数字的和
        {
            cnt ++ ; 
            v[cnt] = a * k ; //当前堆中的物品体积
            w[cnt] = b * k; // 当前堆中的物品价值
            s -= k; 
            k *= 2; // 不断二进制
        }

        if(s>0)     //如果有剩余数字
        {
            cnt ++ ;
            v[cnt] = a*s; 
            w[cnt] = b*s;
        }
    }

（3）分组背包简述

题意：给定n组，一组中各物品体积价值不同且一组只能选一个物品。

思路：简单回顾一下二：状态表示将 $f[i][j]$ 中 i 的含义更新成第 i 组，之前不是第 i 个/第 i 堆物品嘛。这就要求一个二维数组用来存第 i 组中的第 i 个物品。状态计算仍可以认为成01背包问题：要还是不要当前物品，因为一组只能选一个嘛。对于二，之后还会有详细讲解。

代码：

    for(int i=1;i<=n;i++)
        for(int j=m;j>=0;j--)
            for(int k=1;k<=s[i];k++){
                if(j>=v[i][k])
                    f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
            }

Victory_orsh

关注

19
点赞
踩
25

收藏

觉得还不错? 一键收藏
0
评论
那些你不理解的dp背包问题的详解

本文旨在以最通俗易懂的语言讲解动态规划中背包问题的细节问题，这些问题可能成为理解动态规划中的一个个小障碍，这篇文章就是对这类问题的总结归纳，争取实现让读者初步了解dp后可以通过这篇文章学习解决每个疑问，而不是一个个查询消耗热情。
复制链接

扫一扫