多层感知机（MLP）

引入

首先，用一个实际问题来引入感知机的概念。

比如给出很多组数据，每一组数据有身高、体重，让我们进行胖瘦分类，这时候就可以用感知机进行二分类了。

接下来看一下感知机分类的过程。

通过训练数据来不断更新直线的位置，使直线上面是瘦，下面为胖。

最后来看一下定义。

感知机

定义

感知机（Perceptron）是一种简单的二分类线性分类模型，它是机器学习领域的一个经典算法。感知机由美国科学家 Frank Rosenblatt 在1957年提出，被认为是神经网络和支持向量机的基础。

感知机的基本原理是通过计算输入特征的线性组合，然后使用激活函数对结果进行二分类。它的输入是一组实数特征向量 $\mathbf{x}=(x_1,x_2,\dots ,x_n)$ ，每个特征都有相应的权重 $\mathbf{w}=(w_1,w_2,\dots ,w_n)$ ，还有偏移 $\mathbf{b}$ 。感知机的输出 $y$ 是一个二值输出（+1 或 -1），表示输入样本属于哪个类别。

$$o=\sigma (⟨\mathbf{w},\mathbf{x}⟩+b)\sigma (x)=\{\begin{array}{ll}1& \text{ if }x>0\\ 0& \text{ otherwise }\end{array}$$

感知机的目的是 找到一个能够将不同类别的样本正确分类的超平面（对于二维空间，即一条直线），从而实现对新的未知样本的预测。

实现过程

首先就是初始化权重、偏移，和前面的线性回归、Softmax回归不一样（权重为正态分布随机值、偏差为0），权重、偏移的值都为0。

接下来就开始进行训练。

咱们应该明白何为预测结果正确，就是当标签为1时，预测结果 ${\hat{y}}_i$ (未经过激活函数)大于0；标签为-1是，预测结果 ${\hat{y}}_i$ (未经过激活函数)小于等于0。这样预测结果才是准确的！！！

所以当标签 ${\mathbf{y}}_i$ 乘以 预测结果 ${\hat{y}}_i$ 小于等于0时，说明此时的权重、偏移不合理，需要更新。更新方式为 $w\leftarrow w+y_i{x}_i\text{ and }b\leftarrow b+y_i$ 。类似于梯度下降的更新方式。

步骤公式如下

$$\begin{array}{l}\text{initialize }w=0\text{ and }b=0\\ \text{repeat}\\ \text{if }{y}_i\left[⟨w,x_i⟩+b\right]\le 0\text{ then}\\ w\leftarrow w+y_i{x}_i\text{ and }b\leftarrow b+y_i\\ \text{end if}\\ \text{until all classified correctly}\end{array}$$

最后使用损失函数

$$\ell (y,\mathbf{x},\mathbf{w})=max(0,-y⟨\mathbf{x},\mathbf{w}⟩)$$

当 $y⟨\mathbf{x},\mathbf{w}⟩$ 大于0的时候，表示预测结果正确，没有损失；小于等于0的时候，预测结果错误。

多层感知机的引入

感知机可以进行线性可分（与或非等逻辑操作），但是无法进行线性不可分（异或操作），出现了神经网络的第一次寒冬！！！

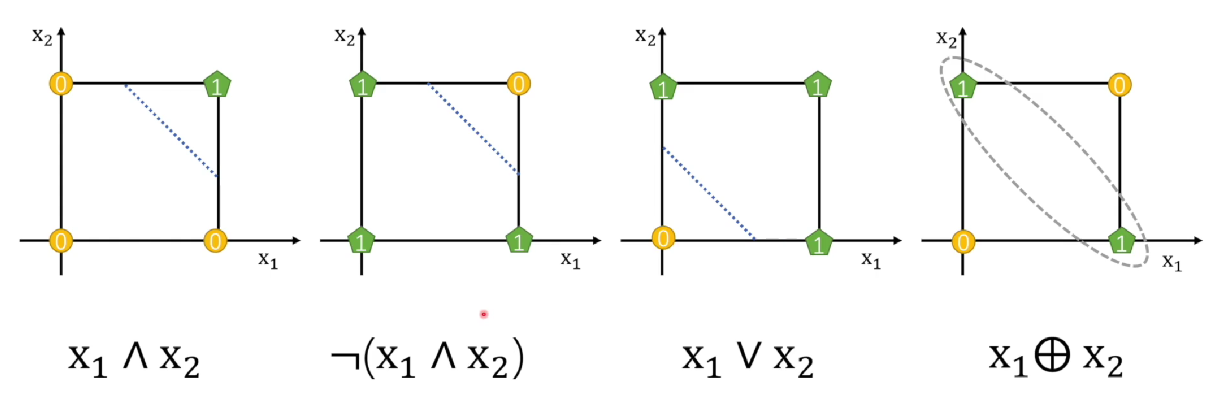
可以看到，前面三个可以通过一条直线分开0、1，最后的异或却无法分开，那么怎么办呢？
由于异或 是 与或非 组合的结果，那么我们可不可以通过多个感知机来实现呢？接下来让我们来看看。

$$x_1\oplus x_2=(\neg x_1\wedge x_2)\vee (x_1\wedge \neg x_2)$$

看样子是可行的，先分别用两个感知机把左右两边解决，最后再用一个感知机进行 或操作。

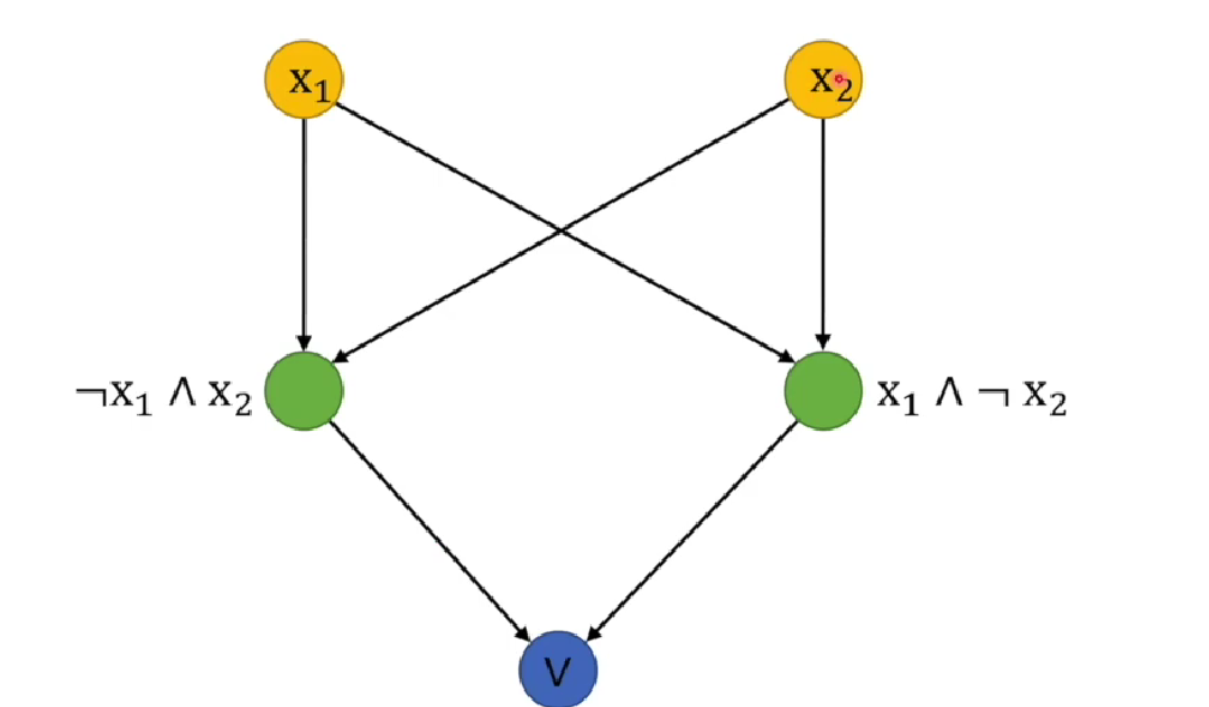
以上内容由 王木头学科学的视频整理而来

什么是“感知机”，它的缺陷为什么让“神经网络”陷入低潮

多层感知机

定义

我们可以通过在网络中 加入一个或多个隐藏层 来克服线性模型的限制， 使其能处理更普遍的函数关系类型。 要做到这一点，最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层，直到生成最后的输出。 我们可以把前 $L-1$ 层看作表示，把最后一层看作线性预测器。 这种架构通常称为多层感知机（multilayer perceptron），通常缩写为MLP。

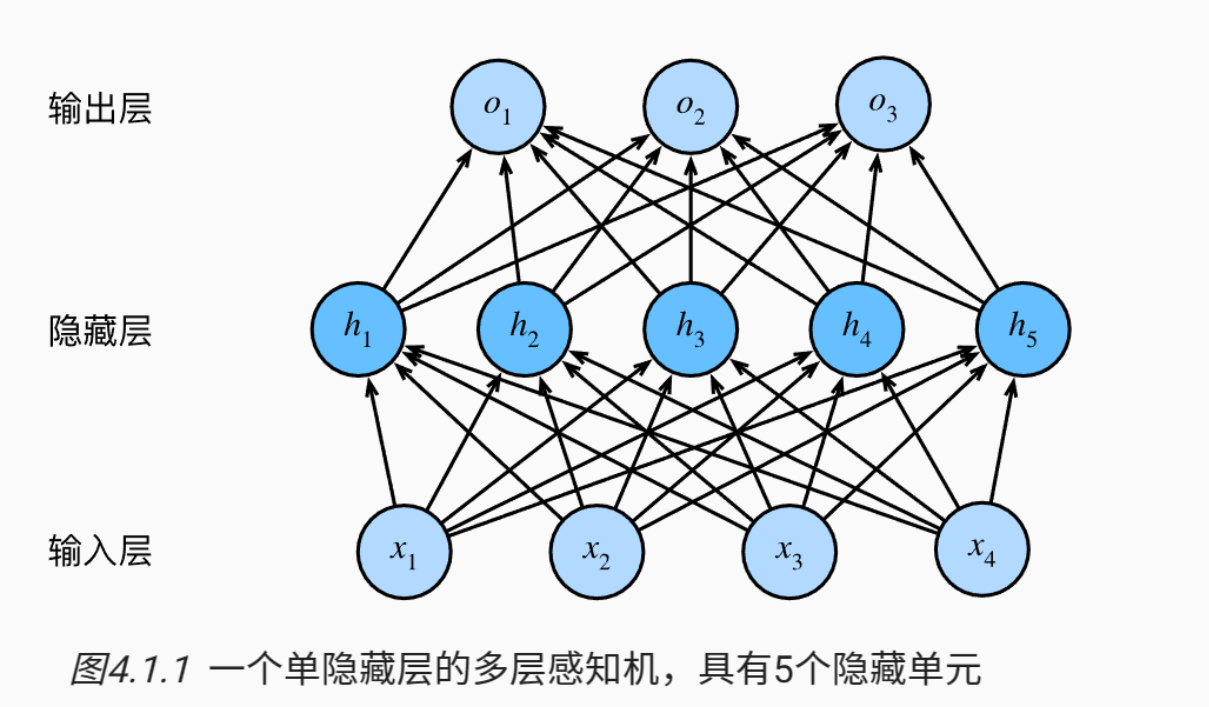
从线性到非线性

现在咱们已经从线性模型过渡到了非线性模型，接下来看看输出是怎么算出来的。
首先，明确一下输入。由于每次是 $n$ 个样本的小批量，每一个样本有 $d$ 个特征，所以输入为 $\mathbf{X}\in {\mathbb{R}}^{n\times d}$。
假设是具有 $h$ 个隐藏单元的单隐藏层多层感知机，那么权重就为 ${\mathbf{W}}^{(1)}\in {\mathbb{R}}^{d\times h}$ ，偏置为 ${\mathbf{b}}^{(1)}\in {\mathbb{R}}^{1\times h}$ ，那么隐藏层的输出为 $\mathbf{H}\in {\mathbb{R}}^{n\times h}$ 。
由于有 $q$ 个类别，所以输出的权重为 ${\mathbf{W}}^{(2)}\in {\mathbb{R}}^{h\times q}$ ，偏置为 $\mathbf{b}\in {\mathbb{R}}^{1\times q}$ ，最后可以得到输出。

$$\begin{array}{rl}\mathbf{H}& =\sigma (\mathbf{X}{\mathbf{W}}^{(1)}+{\mathbf{b}}^{(1)})\\ \mathbf{O}& =\mathbf{H}{\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)}\end{array}$$

其中 $\sigma ()$ 是进行按元素激活函数。
那么为什么需要激活函数呢？
其实很简单，首先咱们把不用激活函数的式子列出来。

$$\mathbf{O}=\left(\mathbf{X}{\mathbf{W}}^{(1)}+{\mathbf{b}}^{(1)}\right){\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)}=\mathbf{X}{\mathbf{W}}^{(1)}{\mathbf{W}}^{(2)}+{\mathbf{b}}^{(1)}{\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)}=\mathbf{XW}+\mathbf{b}$$

这里不难看出，$\mathbf{O}$ 与 $\mathbf{X}$ 还是线性关系，这和单层感知机没有什么区别，就是一个简单的线性模型而已。所以需要加上激活函数，接下来咱们看看有哪些激活函数可以使用。

激活函数

sigmod函数

Sigmoid函数将输入值映射到一个范围为(0, 1)的区间，具有平滑的S形曲线。

$$\mathrm{sigmoid}(\mathrm{x})=\frac{1}{1+\exp (-\mathrm{x})}$$

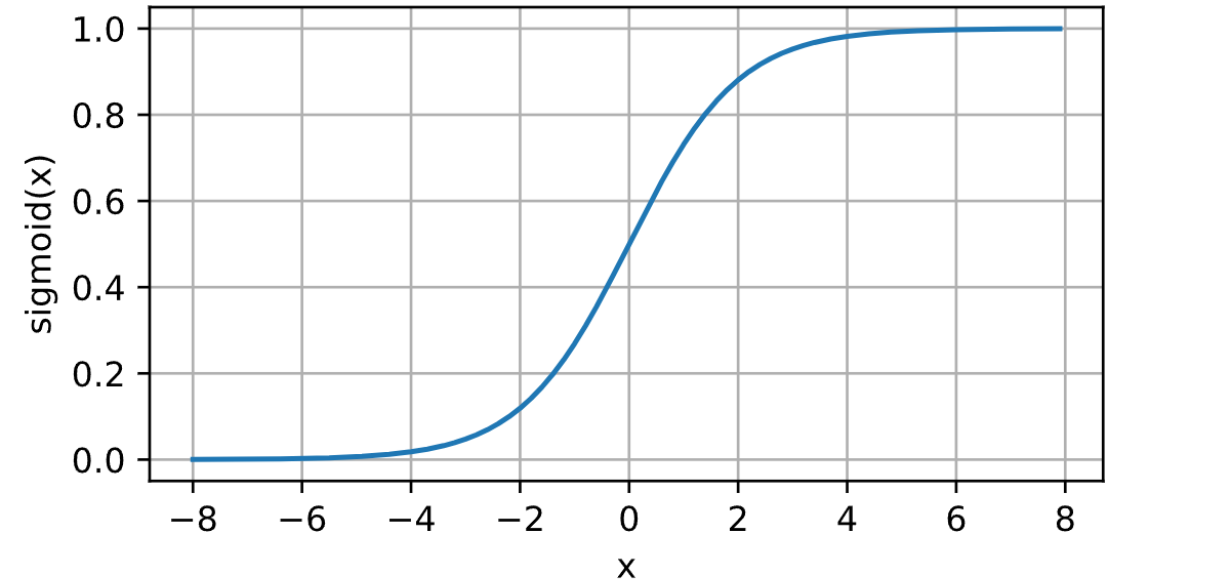
但是是有弊端的。

• 梯度饱和：在Sigmoid函数的两端，梯度接近于0，导致梯度消失问题。这会使得在反向传播时梯度逐渐变小，从而在深度网络中影响参数的更新和收敛速度。

• 输出非零均值：由于Sigmoid函数输出在(0, 1)之间，对于大的负输入，输出接近于0，导致神经元的平均输出值不为0。这可能会对下一层的神经元带来偏置，影响整体网络的学习能力。

tanh函数

tanh函数将输入值映射到一个范围为(-1, 1)的区间，也具有S形曲线。

$$\tanh (\mathrm{x})=\frac{\exp (\mathrm{x})-\exp (-\mathrm{x})}{\exp (\mathrm{x})+\exp (-\mathrm{x})}=\frac{1-\exp (-2x)}{1+\exp (-2x)}$$

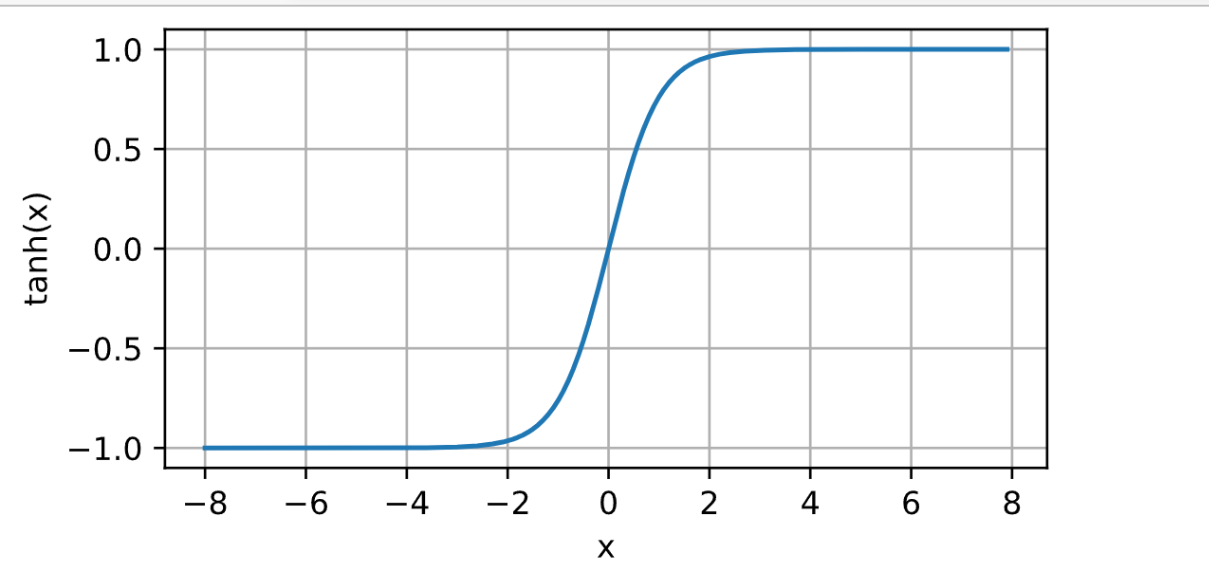
弊端：与Sigmoid函数类似，Tanh函数在两端也存在梯度饱和和输出非零均值的问题，会影响神经网络的训练效果。

ReLU函数

ReLU（Rectified Linear Unit）函数在输入大于0时返回该输入值，小于等于0时返回0

$$\mathrm{ReLU}(\mathrm{x})=\max (0,\mathrm{x})$$

ReLU函数有以下两个特点。

• ReLU函数计算简单高效，不涉及复杂的指数运算。

• ReLU函数解决了Sigmoid和Tanh函数存在的梯度饱和问题，激活函数的导数在正数区域始终为常数1，可以有效传递梯度。

从零实现多层MLP

咱们可以继续对图片进行多分类，看看和线性回归（softmax回归）在精度上有什么变化不。
这一次比前面实现softmax回归简单，上一节侧重点在于让我们知道d2l库封装的一些函数，这次咱们只需要调用即可，忘记的话可以去上一篇文章回忆一下！
softmax回归

读取数据集

还是和之前一样，读取一个批量大小为256的数据集。

!pip install d2l

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size)

初始化参数

这里多了一层隐藏层，大小可以自己设定，建议不要太小 会损失很大有用的信息！这里选择的大小为256

num_inputs,num_outputs,num_hiddens = 784,10,256

W1 = nn.Parameter(torch.rand(num_inputs,num_hiddens,requires_grad = True) * 0.01) # 把随机生成的 [0,1]的张量变为 [0,0.01]
b1 = nn.Parameter(torch.zeros(num_hiddens,requires_grad = True))

W2 = nn.Parameter(torch.rand(num_hiddens,num_outputs,requires_grad = True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs,requires_grad = True))

params = [W1,b1,W2,b2]

定义激活函数

使用ReLU作为激活函数，就是与0比较，取最大值。注意，X为矩阵，所以应该生成和 X 一样的形状大小的0.

def relu(X):
  a = torch.zeros_like(X)
  return torch.max(a,X)

定义模型

此时 $\mathbf{X}$ 为三维（省略了通道数1），形状为 $(28,28,batch\_size)$ ,但是权重是二维的，所以需要给 $\mathbf{X}$ 降维，使用reshape即可

def net(X):
  X = X.reshape((-1,num_inputs))
  H = relu(X @ W1 + b1) #@为矩阵乘法
  return (H @ W2 + b2)

loss = nn.CrossEntropyLoss()

训练

还要调用之前封装好的函数，进行训练，可以看看之前的，要不然不知道函数怎么用

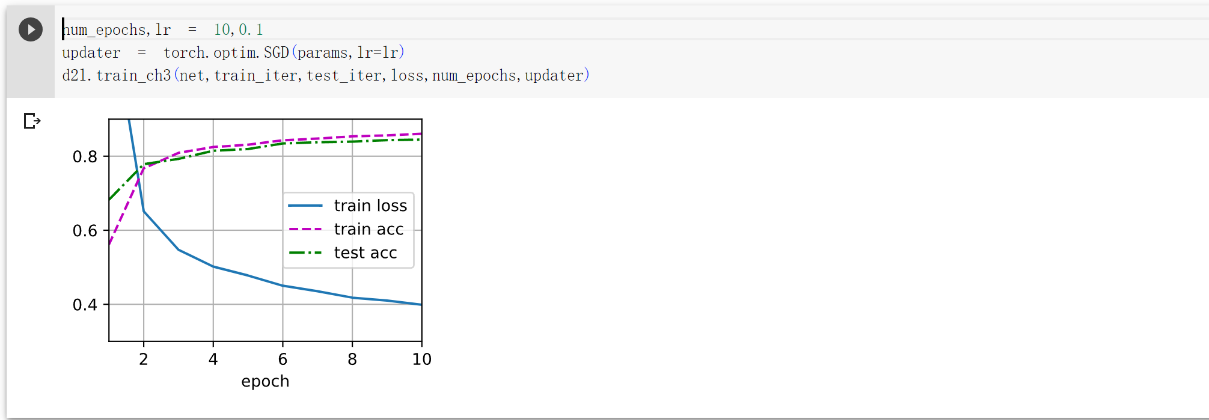
num_epochs,lr = 10,0.1
updater = torch.optim.SGD(params,lr=lr)
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,updater)

预测

d2l.predict_ch3(net, test_iter)

简洁实现

由于和上面一样，直接给出完整代码

!pip install d2l==0.17

import torch
from torch import nn
from d2l import torch as d2l

#定义模型
net = nn.Sequential(nn.Flatten(),
           nn.Linear(784,256),
           nn.ReLU(),
           nn.Linear(256,10))

#初始化权重，没有bios是因为，默认为0
def init_weight(m):
  if type(m) == nn.Linear:
    nn.init.normal_(m.weight,std=0.01)

#应用初始化权重函数
net.apply(init_weight)

batch_size,lr,num_epochs = 256,0.1,10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(),lr = lr)

train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

d2l.predict_ch3(net,test_iter)