c语言表达式求值之隐式类型转换

先算乘除再算加减，有括号的先算括号内的，相信这句小学时学的口诀一直印在我们心中。正如我们小学数学算式计算的那样，c语言表达式也有自己的运算规则。

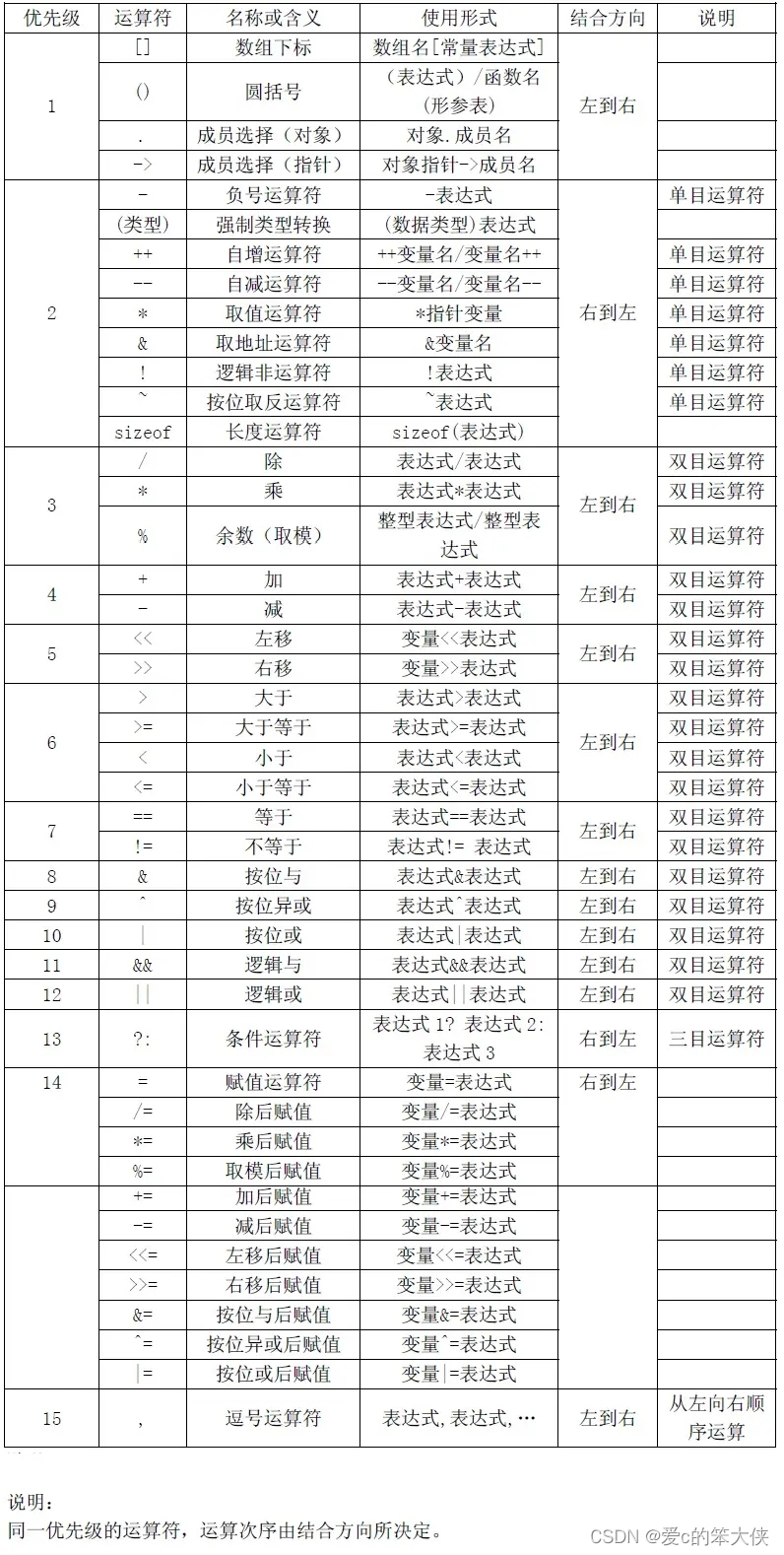
表达式求值是由操作符的优先级和结合性决定。
 

但在运算过程中，不同类型的数据是怎么处理的呢？

一.整型提升

C的整型算术运算总是至少以缺省整型类型的精度来进行的。为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。

表达式的整型运算要在CPU的相应运算器件内执行，CPU内整型运算器(ALU)的操作数的字节长度，一般就是int的字节长度，同时也是CPU的通用寄存器的长度。
因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长
度。
通用CPU（general-purpose CPU）是难以直接实现两个8比特字节直接相加运算（虽然机器指令中可能有这种字节相加指令）。所以，表达式中各种长度可能小于int长度的整型值，都必须先转换为int或unsigned int，然后才能送入CPU去执行运算。

 

对于以下这段代码，求出值很简单，可是计算机是怎么求出的值呢。

 分析如下：

a，b，c三个变量都是char类型的，那么它们所占空间都应该是一个字节。但CPU中的整型运算器操作数确是4个字节。所以为了实现其运算，就需要对其进行整型提升。

a的补码是：

00000001

b的补码是：

00000010

进行整型提升，变为四个字节，这就与运算器相符。

a提升后的补码为：

00000000 00000000 00000000 00000001

b提升后的补码为：

00000000 00000000 00000000 00000010

c = a + b

00000000 00000000 00000000 00000001

+

00000000 00000000 00000000 00000010

=

00000000 00000000 00000000 00000011

但c是char类型，只能存储一个字节，所以就会发生截断，只保留最后的那一个字节。

c的补码是：

00000011

调用printf函数，输出c的时候，需要对c进行整形提升。

c提升后的补码为：

00000000 00000000 00000000 00000011

正数的原码，反码，补码都一样。所以我们就可以得到c的值为3。

---

整型提升的规则：

1.有符号数：

高位补充符号位

1.正数的整型提升

char a=1

00000001

正数的符号位为0，高位用0来补充。

00000000 00000000 00000000 00000001

故，对于正数，高位补0。

2.负数的整型提升

char a=-1

a的原码是：

10000001

a的反码是：

11111110

a的补码是：

11111111

负数的符号位为1，高位用1来补充。

11111111 11111111 11111111 11111111

故，对于负数，高位补1。

ps：

原码→反码：

符号位不变，其余位按位取反

反码→补码：

反码+1

2.无符号数

高位补充0

---

练习：

char a=127，b=5，c=a+b

c应该是多少？132？

127+5=132，按照数学上来说就是这个结果，可是当我们在编译器运行后，却不是这个答案。这时大部分解释是溢出了，然后就不在深入解释了。通过刚才的整型提升，我们来推一遍，就能知道为什么编译器会给出这个答案。

a的补码：

01111111

b的补码：

00000101

a+b运算时发生整型提升：

00000000 00000000 00000000 01111111

+

00000000 00000000 00000000 00000101

=

00000000 00000000 00000000 10000100

储存在c中，发生截断，只保留最低的那个字节。

10000100

对c输出时，进行整型提升

 11111111 11111111 11111111 10000100

数据一补码的形式在计算机中存储，原码是数据的二进制，所以将补码转换成原码，才是呈现在我们面前的数。

反码：

11111111 11111111 11111111 10000011

原码

10000000 00000000 00000000 01111100

所以，输出的c是-124。

通过此练习，我们就可以清楚的知道，编译器到底怎么得出的溢出之后的值。

ps：

补码→反码：

补码-1

反码→原码：

符号位不变，其余位按位取反。

在进行计算时，是通过补码相加减。呈现在我们面前，是通过原码实现。

---

验证：

观察以下代码

 通过sizeof，我们可以测出c的大小是一个字节。但当是+c，-c，这种表达式类型时，大小确变成了4个字节。

因此，我们可以确定，像char，short，这种小于int的，在表达式中都会发生整型提升。 

---

二.算数转换

如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类型，否则操作就无法进行。下面的层次体系称为寻常算术转换。
 

1ong double

double

float
unsigned 1ong int

long int

unsigned int

int

如果某个操作数的类型在上面这个列表中排名较低，那么首先要转换为另外一个操作数的类型后执行运算。

换句话说，就是向字节长的转换，如果字节相同，就向精度高的转换。