何谓数据变换
数据变换指的是对原始数据进行系统性的转换,以改变其形式、结构或分布,从而提高数据的质量和适用性。通过数据变换,可以使数据更适合后续的分析、建模或可视化。
数据变换的目的
1、提高模型性能:通过改变数据的分布,比如将原数据变换成正态分布的数据,使其更符合机器学习模型的假设,从而提高模型的准确性和预测能力。
2、处理不同尺度:标准化或归一化数据,以消除特征之间的量纲差异(单位差异),加快模型的训练速度,确保不同特征对模型的影响均衡。
3、改善数据分布:通过对数变换、平方根变换等方法,减少偏态分布的影响,使数据更接近正态分布。
4、降低异常值的影响:一些变换可以减小异常值对模型的干扰,例如对数变换可以压缩数据范围,从而降低异常值的影响。
5、增加数据的可解释性:通过合适的变换,可以使数据的特征更具可解释性,帮助分析者更好地理解数据背后的模式。比如将数值型的年龄数据离散化,分成青年、中年、老年,可以更好地解释模型。
数据变换的局限性
1、信息损失:某些变换(如对数变换、分位数变换、离散化)会导致数据的精细信息丢失。特别是分位数变换和离散化会导致数据之间的原始顺序关系或细微差异消失,可能影响模型性能。
2、对异常值的敏感性:一些变换(如最小-最大归一化)对异常值敏感,可能导致特征范围受异常值极端拉伸,影响归一化效果。即便在异常值处理后,某些变换仍可能被极端值干扰。
3、不适合某些数据分布:一些变换方法(如Z-score标准化)假设数据分布为正态分布,因此不适合高度偏态数据。即便是Box-Cox和Yeo-Johnson变换,也需要数据分布接近正态才有最佳效果。
4、计算复杂性:某些变换(如分位数变换和Yeo-Johnson变换)计算复杂度较高,特别是在大规模数据集上,可能显著增加计算时间和资源消耗,不适合实时应用。
5、模型依赖性:不同模型对数据分布的敏感程度不同,比如线性模型和神经网络对数据的分布较敏感,而决策树等模型对数据分布相对不敏感。
6、无法改善非线性关系:变换主要是调整数据的分布或尺度,无法处理数据中潜在的非线性关系。对非线性问题,即便变换后,数据仍然可能不能很好地满足模型假设,导致效果欠佳。
7、过度变换:在一些情况下,对数据进行过多变换会导致模型失去对原始数据的直观理解能力,特别是对需要解释性的数据应用而言,可能会使结果难以解释。
8、依赖变换参数:如Box-Cox和Yeo-Johnson变换需要选择合适的参数以获得良好效果。这些参数通常需要根据数据具体情况调整,因此具有一定不确定性,如果选取不当,可能会导致模型性能下降。
常见的数据变换方法
(一)标准化和归一化
在数据预处理中,“归一化”是一个广义的概念,指的是将数据调整到统一的尺度。归一化是一个更为广泛的概念,而标准化是其中的一个特定方法。常见的归一化方法:
1、最小-最大归一化
其中,X是原始数据,Xmin 和 Xmax 分别是该特征的最小值和最大值。归一化后的数据范围在 [0, 1] 之间。
2、标准化(也叫Z-score标准化)
μ是特征的均值,σ是特征的标准差。归一化后的数据的均值为0,标准差为1。对符合正态分布的数据尤为适用。
3、Robust Scaling
Robust Scaling 是一种特殊的归一化方法,适用于包含异常值的数据。它的核心思想是通过中位数和四分位距来缩放数据,从而降低异常值的影响,使得数据分布更加稳定。
(二)对数变换
对数变换是一种常用的数据变换方法,主要用于处理非正态分布的数据,或解决方差不齐等问题。基本思想是将数据的每个值取对数,以便减少数据的偏态,改善数据的分布特征。常见的对数变换包括自然对数(以e为底)、常用对数(以10为底)和二进制对数(以2为底)。
![]()
局限性:由于对数只能处理正值,所以原数据只能包含正值,或者将数据平移使数据都变为正值。
(三)Box-Cox变换
Box-Cox变换是一种用于使非正态分布数据趋向正态分布的统计方法。这种变换可以改善数据的线性关系、方差齐性和正态性,从而使得许多统计分析方法(如回归分析)更加有效。
选择适当的λ值:通常通过对数据进行最大似然估计来选择λ的值。
极大似然函数求λ值(即优化λ取值):
1、假设变换后的数据服从正态分布N(μ,σ2),则似然函数可以写为:
2、取对数似然函数(μ和σ可以写成包含λ的表达式,故只有λ一个参数未知):
3、直接求最小的对数似然函数值比较困难。可以利用网格搜索,代入不同λ,计算出对应的对数似然函数值
4、最大的对数似然值对应的λ值就是最终的λ(作为近似最优解)。得出λ就可以进行数据变换了。
(四)yeo-Johnson变换
Yeo-Johnson变换是一种数据变换技术,常用于对非正态分布的数据进行变换,以接近正态分布。与Box-Cox变换类似,Yeo-Johnson变换的目的也是减少数据的偏度,帮助提高模型的准确性、稳定性,特别是在机器学习和统计建模中。相比于Box-Cox变换,Yeo-Johnson变换允许数据包含负值,尤其适合用于包含负值和严重偏态的数据,从而具有更广泛的适用性。

选取λ的方式与Box-Cox变换类似。
(五)分位数变换
分位数变换是一种非参数的统计方法,旨在将数据集转换为一个新的分布,以便适应特定的分析需求,常见应用是将数据调整为正态分布。
1、排序数据:将数据集的数据按从小到大的顺序排列。例如:排序后数据为
[2, 5, 10, 11, 15]2、计算分位数。对应分位点分别为:[
1/6, 2/6, 3/6, 4/6, 5/6]
3、映射分位数至目标分布(关键)。比如,将原始数据的分位数位置映射到正态分布,可以使用标准正态分布的分位数函数(逆累积分布函数)。得到近似正态值[−0.967,−0.432,0,0.432,0.967]
其中p为概率。由于没有简单的解析表达式,逆累积分布函数一般是通过数值方法近似计算的。大部分编程语言和统计软件中都内置了计算逆累积分布的函数。
(六)离散化
数据离散化是将连续数值型数据转换为离散型数据的一种技术,常用于数据预处理和特征工程中。常见的离散化方法:
1、等宽离散化:将数据区间分为若干个相等宽度的区间。每个区间的范围是相同的。
2、等频离散化:将数据分为若干个区间,使得每个区间包含相同数量的数据点。
3、聚类离散化:使用聚类算法(如 K-means)将数据点分组,并将每个组视为一个离散类别。
4、自定义离散化:根据业务需求或领域知识手动定义离散化规则,例如将年龄分为“儿童”、“青少年”、“成人”和“老年人”。
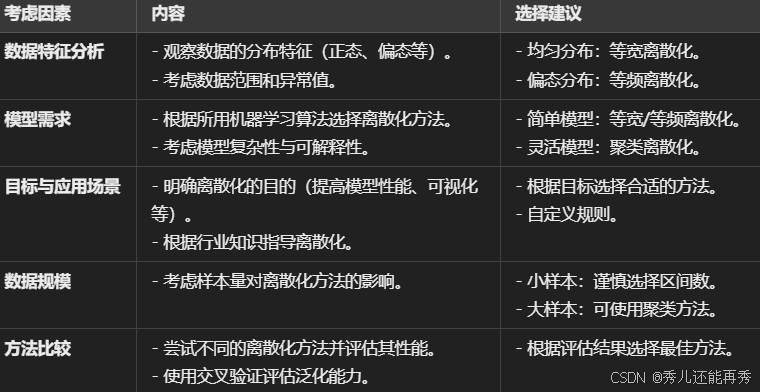
离散化方法选择:
数据变换方法的应用场景总结












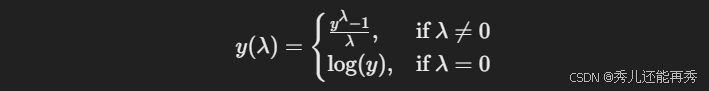






















 893
893

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








