统计特征：偏度和峰度（可视化图例解释）

最新推荐文章于 2025-05-18 13:20:48 发布

秀儿还能再秀

最新推荐文章于 2025-05-18 13:20:48 发布

阅读量4.9k

点赞数 26

文章标签：大数据数据分析 python 学习笔记

本文链接：https://blog.csdn.net/weixin_74268817/article/details/143508352

版权

基本概念

在机器学习和数据分析中，峰度和偏度可以作为特征提取的指标，用于评估数据的分布形状，从而帮助理解数据集的特征并选择合适的模型。

峰度：衡量数据分布的尖锐程度或尾部的厚度。

高峰度：分布曲线尖锐，尾部较重，峰度较高，表示更多极值。
常态峰度：类似正态分布，峰度接近零。
低峰度：分布曲线较平缓，尾部轻，峰度较低，数据更分散。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import kurtosis

plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体字体
plt.rcParams['axes.unicode_minus'] = False  # 处理负号显示
# 设置随机种子
np.random.seed(0)

# 生成不同高峰度的数据
data_h= np.random.laplace(loc=0, scale=1, size=1000)  # 高峰度分布
data_n = np.random.normal(loc=0, scale=1, size=1000)    # 常态峰度分布
data_l = np.random.uniform(low=-2, high=2, size=1000)   # 低峰度分布

# 计算高峰度
kurt_h = kurtosis(data_leptokurtic)
kurt_n = kurtosis(data_mesokurtic)
kurt_l = kurtosis(data_platykurtic)

# 绘图
plt.figure(figsize=(12, 6))

# 高峰度分布
plt.subplot(1, 3, 1)
sns.histplot(data_h, bins=30, kde=True, color='blue', stat='density')
plt.title('高峰度分布')

# 常态峰度分布
plt.subplot(1, 3, 2)
sns.histplot(data_n, bins=30, kde=True, color='green', stat='density')
plt.title('常态峰度分布')

# 低峰度分布
plt.subplot(1, 3, 3)
sns.histplot(data_l, bins=30, kde=True, color='red', stat='density')
plt.title('低峰度分布')  # 修正了这个标题

plt.tight_layout()
plt.show()

偏度：衡量数据分布的对称性或偏斜方向。

正偏 (右偏)：右偏分布指的是数据分布的尾部向右侧延伸，即较高的值（极端值）分布在右侧。此时，均值通常大于中位数。
负偏 (左偏)：左偏分布指的是数据分布的尾部向左侧延伸，即较低的值（极端值）分布在左侧。此时，均值通常小于中位数。
对称 (无偏)：分布呈对称形状，类似于正态分布，偏度接近零。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import skew

# 设置字体以支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体字体
plt.rcParams['axes.unicode_minus'] = False  # 处理负号显示

# 设置随机种子
np.random.seed(0)

# 生成不同偏度的数据
data_r = np.random.exponential(scale=1, size=1000)  # 右偏分布
data_l = -np.random.exponential(scale=1, size=1000)  # 左偏分布
data_n = np.random.normal(loc=0, scale=1, size=1000)  # 对称分布

# 计算偏度
skew_r = skew(data_r)
skew_l = skew(data_l)
skew_n= skew(data_n)

# 绘图
plt.figure(figsize=(15, 5))

# 右偏分布
plt.subplot(1, 3, 1)
sns.histplot(data_r, bins=30, kde=True, color='blue', stat='density')
plt.title(f'右偏分布 (偏度: {skew_r:.2f})')

# 左偏分布
plt.subplot(1, 3, 2)
sns.histplot(data_l, bins=30, kde=True, color='green', stat='density')
plt.title(f'左偏分布 (偏度: {skew_l:.2f})')

# 对称分布
plt.subplot(1, 3, 3)
sns.histplot(data_n, bins=30, kde=True, color='red', stat='density')
plt.title(f'对称分布 (偏度: {skew_n:.2f})')

plt.tight_layout()
plt.show()

检验方法

1、可视化方法（主观判断）

直方图：

偏度：直方图的形状可以显示数据分布的偏斜程度。如果左侧尾巴较长，说明数据左偏；如果右侧尾巴较长，说明数据右偏。

峰度：直方图的尖峭程度可以反映峰度。如果直方图的形状很尖，则可能具有高峰度；如果形状比较平坦，则可能具有低峰度。

结合偏度和峰度一起判断。

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体字体
plt.rcParams['axes.unicode_minus'] = False  # 处理负号显示
np.random.seed(10)

# 示例数据
data = np.random.normal(loc=50, scale=10, size=200)
data = np.append(data, [150, 160, 180])  # 添加异常值

# 绘制直方图
plt.hist(data, bins=30, edgecolor='black')
plt.title("直方图")
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.show()

箱线图:

偏度：可以判断。通过观察箱体的对称性和须的长度，可以判断数据的偏度。如果箱体的中位线偏向一侧，或一侧的须较长，说明数据存在偏斜。

峰度：不直接判断。箱线图主要显示数据的四分位数和极端值，不能直接判断峰度。

# 示例数据
data = np.random.normal(loc=50, scale=10, size=200)
data = np.append(data, [150, 160])  # 添加异常值

# 绘制箱线图
sns.boxplot(data=data)
plt.title("箱线图")
plt.show()

QQ图:

偏度：可以间接判断。QQ图通过将样本分位数与理论分布的分位数进行比较，偏离直线的程度可以间接反映数据的偏度。

峰度：可以判断。QQ图的偏离程度也可以用来判断峰度。如果尾部比理论分布的尾部更重，说明数据的峰度较高。

# 生成示例数据
data3 = np.random.normal(loc=50, scale=10, size=200)
data3 = np.append(data, [150, 190])  # 添加异常值

# 绘制QQ图
stats.probplot(data3, dist="norm", plot=plt)   # dist="norm"，表示与正太分布比较
plt.title("QQ")
plt.show()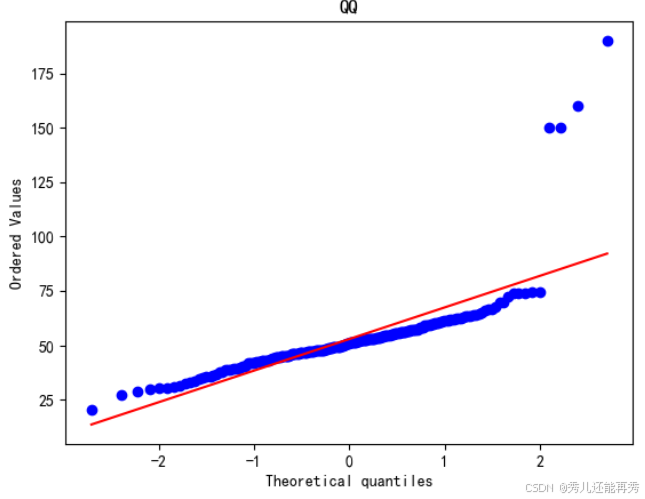

2、统计方法（调包）

import numpy as np
import pandas as pd
from scipy.stats import skew, kurtosis

# 生成一个示例数据集
data = np.random.normal(loc=0, scale=1, size=100)  # 正态分布数据

# 计算偏度和峰度
skewness_ = skew(data)
kurtosis_ = kurtosis(data)   # 默认计算修正峰度
print(f"偏度: {skewness_:.4f}")
print(f"峰度: {kurtosis_:.4f}")

# 偏度: 0.2053
# 峰度: 0.0802

偏度的绝对值通常被认为是：

[0, 0.5]：分布近似对称。

[0.5 , 1]：轻微的偏斜。

[>1 ]：明显的偏斜。

正常峰度（以3为界点）：

峰度 = 3：正态峰度。

峰度 > 3：高峰度（比正态更尖锐）。这通常意味着存在更多的极端值（异常值）。

峰度 < 3：低峰度（比正态更平坦）。这表明数据的极端值较少，数据分散更广。

修正峰度（正常峰度-3，即以0为界点）：

修正峰度 = 0：正态峰度

修正峰度 > 0：高峰度

修正峰度 < 0：低峰度

高峰度

高峰度的特征

分布的集中性更强：高峰度分布说明大部分数据值集中在均值附近，数据密度较高。这通常意味着中间的值变化较小，而多数数据点更靠近均值。
极端值更多：高峰度分布在尾部有更多的极端值或离群点，即数据中包含更多异常的高值或低值。
偏离正态分布：对于假设数据正态分布的模型来说，高峰度可能影响结果的准确性或鲁棒性。

高峰度处理方法

去除异常值：这种方法简单有效，但可能导致信息丢失。
变换数据：对数据进行变换，如使用对数变换、平方根变换或Box-Cox变换，以减小异常值影响。
聚合数据：将数据分组并计算组内的均值或中位数，从而降低异常值的影响。
数据插补：如果异常值影响了模型的表现，可以考虑用插补方法（如均值、邻近值或插值法）来替换异常值。
利用模型鲁棒性：使用对异常值不敏感的模型，如决策树或随机森林。这些模型可以更好地处理高峰度数据。

低峰度

低峰度的特征

分布平坦：低峰度表明数据值的分布较为平坦，数据的集中性较弱。与高峰度相比，数据点分散得更广，意味着均值附近的数据点不如高峰度分布那样密集。
极端值较少：低峰度分布通常在尾部表现出较少的极端值或离群点。这意味着数据中不太可能包含异常的高值或低值，整体上显得更加“正常”。
信息量更均匀：低峰度分布表示信息在不同值之间更均匀地分布，而不是集中在某些特定值上。这种特征可能会影响数据的特征选择和模型构建，因为它可能会导致某些特征的影响力被低估。

低峰度处理方法

增加样本量：收集更多数据，以提高数据集中程度，减少扁平化效应。
特征工程：进行特征选择或构造新特征，增强模型对数据中重要特征的捕捉能力。
使用非参数方法：考虑使用非参数检验或建模方法（如决策树），这些方法对数据分布的假设要求较低。
归一化或标准化：将数据进行归一化或标准化，帮助数据更好地适应模型。
考虑多模型集成：结合不同模型的预测结果，可以帮助提升在低峰度数据上的表现。

左偏和右偏

左偏特征

集中低值：大多数数据值集中在较低的数值上，分布的“峰”偏向左侧。

极端值：存在一些较高的极端值，这些值会拉高均值。

数据分布形态：典型的右偏分布包括指数分布、泊松分布和某些类型的正态分布（如对数正态分布）。

示例：收入分布。大多数人的收入较低，但少数人拥有非常高的收入，导致整体分布右偏。

右偏特征

集中高值：大多数数据值集中在较高的数值上，分布的“峰”偏向右侧。

极端值：存在一些较低的极端值，这些值会拉低均值。

数据分布形态：典型的左偏分布包括某些类型的正态分布和对数分布。

示例：考试成绩分布。大多数学生成绩较高，但可能有少数学生的成绩非常低，导致整体分布左偏。

左偏处理方法

左偏、右偏处理方法

数据变换：

                1、对数变换：对右偏数据进行对数变换可以有效减小偏度，使数据更接近正态分布。

                2、平方根变换：适合于计数数据，能够减少偏度的影响。

                3、反向变换：使用反函数（例如 y=1/x）来处理极端高值，使用反函数（例如y=−x）

                                        来处理极端低值。

去除离群点：通过 Z-score 或 IQR 方法识别和去除极端值，以降低极端值对整体分析的影响

数据分组：将数据分组或分桶，例如使用类别变量来代替原始数值，减少极端值的影响。

模型选择：或者使用适合左偏或右偏分布的模型。