多元函数的基本概念——“高等数学”

各位CSDN的uu们你们好呀，今天，小雅兰的内容是多元函数的基本概念，下面，让我们一起进入多元函数的世界吧

---

平面点集

多元函数的概念

多元函数的极限

多元函数的连续性

有界闭区域上多元连续函数的性质

---

平面点集

第一个是坐标平面

一个平面，在由x轴、y轴所组成的平面直角坐标系内，也就是说在平面直角坐标系中，就叫坐标平面。 

 第二个就是平面点集了

第三个是邻域

 

 

第四个是点与点集的关系

分为内点、外点、边界点、边界、聚点

 

 

由点集所属点的特征

分为开集、闭集、连通集、非连通集

 举两个例子：

 

区域：连通的开集 

闭区域：开区域连同其边界一起构成的点集

下面，来看两个例子：

 有界集、无界集

---

 多元函数的概念

引例

 

 定义

值域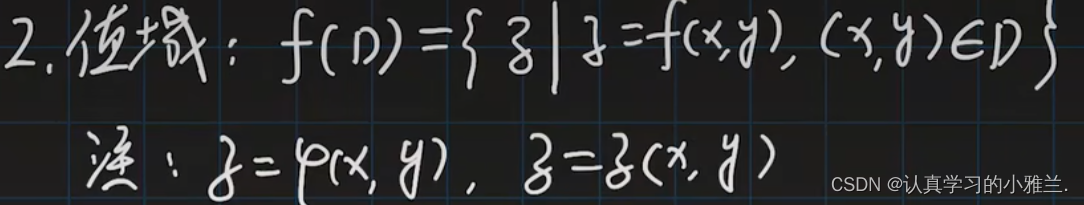 

 推广

自然定义域：使等式有意义的点的集合

二元函数z=f（x，y）的圆形 

 

这样一个三元方程的形式，就是空间中的这样一个曲面 

---

 多元函数的极限

首先，我们先来看看一元函数的极限：

具体的定义：

 注意事项

下面，来看一个例题：

  

 

 

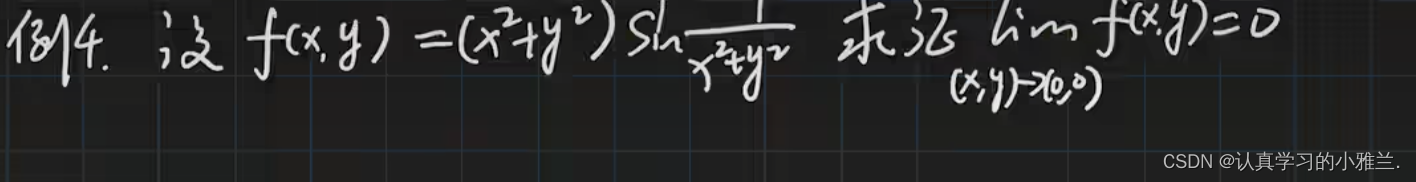
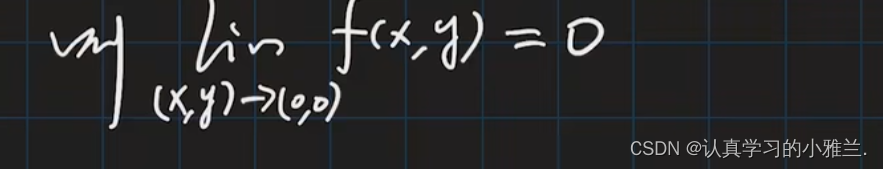
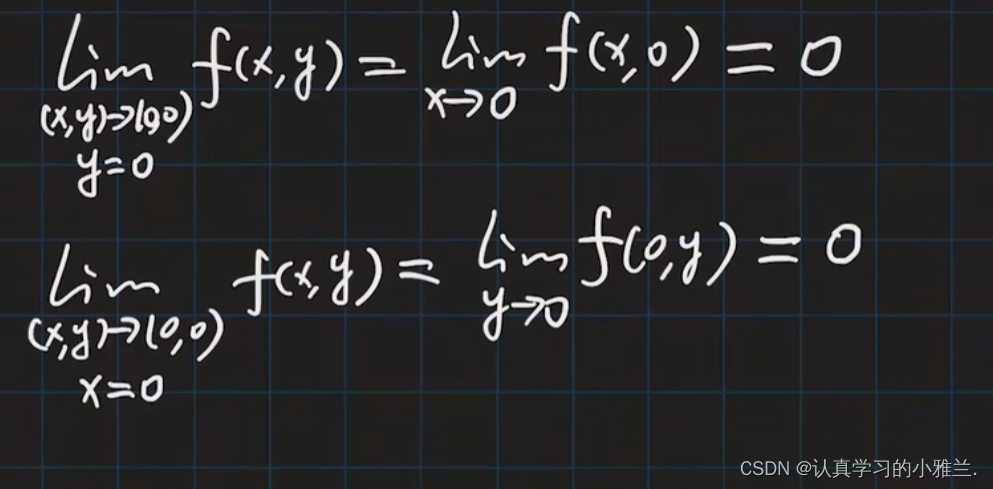
 下面，来看一个例题：

---

 多元函数的连续性

还是以一元函数的连续性为例：

连续的定义

  

 下面，还是来看一个例题：

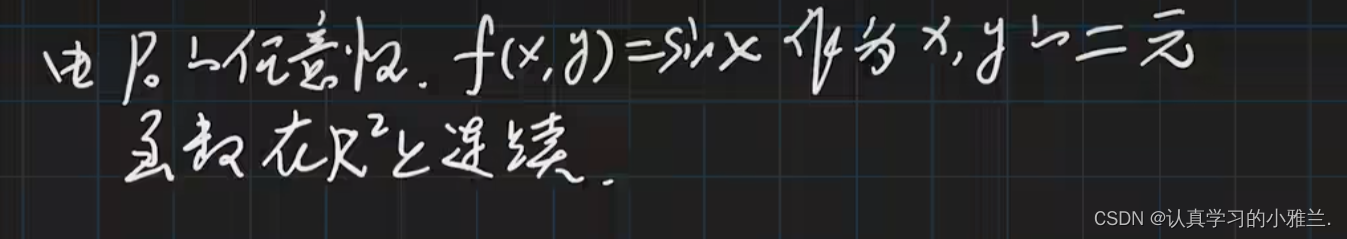
间断点定义 

 

  

下面，来看几个例题：

---

 有界闭区域上多元连续函数的性质

 有界性与最大值、最小值定理

介值定理 

---

 好啦，小雅兰今天的内容就到这里啦，还要继续学习高数噢，希望能过校赛！！！