稳重的DFS学习

wenzhongdehui

已于 2025-04-09 22:49:24 修改

阅读量956

点赞数 27

文章标签：深度优先学习算法 c++

于 2025-04-09 11:21:48 首次发布

本文链接：https://blog.csdn.net/wenzhongdehui/article/details/147072121

版权

(题目的意思是我wenzhong的DFS学习，被我骗进来了吧）

蓝桥杯考试在即，真的贼慌，找了点题刷了刷，更慌了，尤其是做了14年B组真题，感觉自己去了就是炮灰，本来想着发个线性dp和背包dp的文章，结果做题的时候发现，自己连dfs都不会，吓得我连忙来写个dfs学习巩固一下

注：以下学习过程，如果在数据结构课上老师讲过图的基本dfs（我破二本老师都会讲，应该所有老师都会讲吧，不会的看这里），对于理解起来应该简单些，但是我毕竟想要打蓝桥杯，所以写的东西偏向于算法。

（其实无论怎么样，dfs都是一种搜索的算法，基本上会把所有的可能都会访问到，所以这种算法的时间复杂度肯定很高，一般来说会是n的阶乘，甚至是n^n，数值一般不会太大，数据范围差不多就是10）

越是做dfs越能感觉得到，dfs就是一种栈的思想，先进后出

那么废话不多说，上题目辣

第一题

题目源地址

P1784 数独

题目描述

数独是根据9*9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫内的数字均含 1 - 9 ，不重复。每一道合格的数独谜题都有且仅有唯一答案，推理方法也以此为基础，任何无解或多解的题目都是不合格的。

芬兰一位数学家号称设计出全球最难的“数独游戏”，并刊登在报纸上，让大家去挑战。

这位数学家说，他相信只有“智慧最顶尖”的人才有可能破解这个“数独之谜”。

据介绍，目前数独游戏的难度的等级有一到五级，一是入门等级，五则比较难。不过这位数学家说，他所设计的数独游戏难度等级是十一，可以说是所以数独游戏中，难度最高的等级。他还表示，他目前还没遇到解不出来的数独游戏，因此他认为“最具挑战性”的数独游戏并没有出现。

输入格式

一个未填的数独。

输出格式

填好的数独。

输入输出样例

输入
8 0 0 0 0 0 0 0 0
0 0 3 6 0 0 0 0 0
0 7 0 0 9 0 2 0 0
0 5 0 0 0 7 0 0 0
0 0 0 0 4 5 7 0 0
0 0 0 1 0 0 0 3 0
0 0 1 0 0 0 0 6 8
0 0 8 5 0 0 0 1 0
0 9 0 0 0 0 4 0 0

输出
8 1 2 7 5 3 6 4 9
9 4 3 6 8 2 1 7 5
6 7 5 4 9 1 2 8 3
1 5 4 2 3 7 8 9 6
3 6 9 8 4 5 7 2 1
2 8 7 1 6 9 5 3 4
5 2 1 9 7 4 3 6 8
4 3 8 5 2 6 9 1 7
7 9 6 3 1 8 4 5 2

理解一下题意，直接上代码

#include<bits/stdc++.h>
using namespace std;
vector<vector<int>> dt(10,vector<int>(10,-1));
//检查函数，什么？检查什么??你说检查什么!!!
bool check(int x,int y,int n){
    // 检查行
    for(int j=1;j<=9;j++)
        if(dt[x][j]==n) return false;
    // 检查列
    for(int i=1;i<=9;i++)
        if(dt[i][y]==n) return false;
    // 检查3x3宫格
    int bx=(x-1)/3 * 3+1, by=(y-1)/3 * 3+1;
    for(int i=0;i<3;i++)
        for(int j=0;j<3;j++)
            if(dt[bx+i][by+j]==n) return false;
    return true;
}

void dfs(int x,int y,bool& f){
    //顺序4，补全特殊情况
    if (f)return ;
    if (x==10) {
        f=true;
        return;//正常退出位置，说明找到了
    }

    /*但是聪明的你发现了，回溯的时候不会执行这一句
    解决方法两种，第一种转变为bool,在循环过程中加一个return
    第一种改变代码太多，我直接写第二种,增加一个标识的变量*/


    //这一步可以放在循环里面去写，写在外面是因为我改代码的时候拿出来测试错误了
    //感官上来说，更清晰一点不是吗
    //这一步是给下一个调用的dfs的坐标位置
    int xx = x, yy = y + 1;
    if (yy == 10) {
        xx++;
        yy = 1;
    }
    //顺序3，给空位置赋值
    if (dt[x][y]==0){
        for(int i=1;i<=9;i++){ //进行赋值操作

            if(check(x,y,i)){
                dt[x][y]=i;

                dfs(xx,yy,f);//写到这一步会不会有空虚的感觉
                //别急还没写完，用样例开始走一遍代码会发现漏洞百出

                if(f) return;//这一步难以理解，我写的这个变量f很不好，可是我想不到什么好办法

                dt[x][y]=0;//顺序4，回溯

            }//层层递归就会发现，这一段就有栈的思想，一直调用先进入的最后出去，最后调用的先出去
             //其实感觉这一段才是主要核心，其他地方，可以背模版
        }
    }else 
        dfs(xx,yy,f);//继续下一个为止

    return;//未能找到符合条件的，只能被迫退出
}
int main(){
    for(int i=1;i<=9;i++)
        for(int j=1;j<=9;j++)
            cin>> dt[i][j];
    //顺序1，cin数据

    bool f=false;
    dfs(1,1,f);//顺序2.建立dfs,确定起始位置,false不知道是干什么的可以先往后看

    if (f){
        for(int i=1;i<=9;i++){
            for(int j=1;j<=9;j++)
                cout << dt[i][j]<<" ";
            cout<<endl;
        }
    }else cout << "想什么呢，肯定是代码错了";

}
//恭喜你看完了我写的一大堆，如果你觉得加一个bool f太麻烦，有没有更简单的方法
//那我只能说，有的兄弟有的:exit(-1);慎用慎用

（那么通过这个例子，有没有内种先进后出的感觉，实际是算是一种递归的路径）

（其实我写代码之后RE了，最后找AI帮看的代码，你们可以猜一下是哪里RE（Runtime Error））

第二题

题目源地址

P1706 全排列问题

题目描述

按照字典序输出自然数 1到 n 所有不重复的排列，即数列n 的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

输入格式

一个整数 n。

输出格式

由 1到n 组成的所有不重复的数字序列，每行一个序列。

每个数字保留 5 个场宽。

输入

3

输出
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

理解一下题目，直接上代码

#include<bits/stdc++.h>
using namespace std;
int n;
void dfs(vector<int>& nums,vector<bool>& v,int f){
    if (f==n) {
        for(int i=0;i<n;i++){
            cout  << "    " << nums[i];//这是特殊要求的输出格式
        }
        cout << endl;
        return;
    }
    for(int i=1;i<=n;i++){
        if (v[i]){
        	v[i]=false;//标记当前位置的数已经用的，下次dfs的时候就不要再用了
            nums[f]=i;

            dfs(nums,v,f+1);
            //这个f+1也是一个要理解的地方，因为暗含了回溯
            
            //回溯，记得回溯啊宝贝
            v[i]=true;
        }
    }
    return;
}
int main(){
    cin >> n;
    vector<int> nums(n,0);
    vector<bool> v(n+1,true);
    //这个标记数组的概念，可以自己拿样例试一遍，代码就是带着例子过一遍就看懂了

    //这个dfs分别送入了排列数组,标记数组 并且 新增了一个量 来表示v数组下标 会在代码中实时更新（维护了一个变量）
    dfs(nums,v,0);
    return 0;
}

（那么勤奋爱学，聪明机智的你，是否再一次感受到了栈的感觉，但是感觉又不完全一样，感觉像什么呢……树!!!!）

恰好笔者有一个全排列题的图可供参考

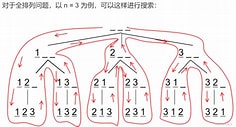
（我觉得非常的生动形象）

那么好那么好，我觉得你肯定可以感觉得到，这两个题，存在基本一致的地方

整理归纳

(类型) dfs （传入数据）{

终止条件

主体{

按照题目要求的写

再次递归调用dfs

回溯

}

return；//这个return也很重要

}//看吧，模版很短吧

传入数据：可选择的有很多，数独的题传入的xy是位置，全排列是一个数组，而且都存在一个标记v，f，可以写入的还有很多，但是根据我的经验来说，尽量就这两个，一个是位置，一个是需求的东西，其他杂七杂八的越写越乱

终止条件：像数独，把9*9的格子填完之后，会填写第十行，这个就是终止条件。全排列也简单，最长就只能排列n个数，多了就是终止

主体：这个应该就是最难的部分，要考虑的东西很多，包括回溯也在这一部分，这一部分太重要了，数独的这一部分就是，如果dfs到的这个格子没有被赋值，那我就尝试赋值继续进行dfs测试是否可行。全排列这一部分是选一个未被选择的数，进行排列，不断返回找出排列的不同结果。

以上初步养成一个规律，先读题，理解题（利用树的结构图是肢解题目过程中需要递归的地方），套用模版，逐步分析传入数据，终止条件和主体部分，完善并优化代码（回溯过程，标记数组，需求结果）

写完以上东西，感觉自己强的不可理喻，上难度上难度

第三题

原题链接

P1219 [USACO1.5] 八皇后 Checker Challenge

题目描述

一个如下的6*6的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

上面的布局可以用序列2 4 6 1 3 5来描述，第 i 个数字表示在第 i 行的相应位置有一个棋子，如下：

行号 1 2 3 4 5 6

列号 2 4 6 1 3 5

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前3 个解。最后一行是解的总个数。

输入格式

一行一个正整数 n，表示棋盘是 n*n 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入
6

输出
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

数据范围 (6<=n<=13)

（有没有感觉跳跃幅度很大，其实就是未能完全的理解题）

（先抽象一遍题意，在棋盘上放置棋子，放置的时候要保证，棋子不在其他棋子的同一行，同一列，同一对角线，其实规则就是，棋子是世界象棋的皇后，在棋盘上放置n个皇后，要求皇后之间不可以互相吃到，题目名也叫八皇后嘛。最后归纳一下，我要在棋盘上放置皇后，保证皇后之间不可以互相吃，找出每一种可以摆放的可能性，并输出前三种可能和全部可能的总数）

先看我错误的代码

#include<bits/stdc++.h>
using namespace std;
int ans=0;int n;
void check(int x,int y,vector<vector<bool>>& v){
    //同行同列标记成false
    for(int i=1;i<=n;i++){
        v[x][i]=false;
        v[i][y]=false;
    }
    //对角线标记成false
    //八向标记，斜向
    for(int i = 1; i <= n; i++) {
        if(x-i >= 1 && y-i >= 1) v[x-i][y-i] = false; // 左上
        if(x+i <= n && y+i <= n) v[x+i][y+i] = false; // 右下
    }
    for(int i = 1; i <= n; i++) {
        if(x-i >= 1 && y+i <= n) v[x-i][y+i] = false; // 右上
        if(x+i <= n && y-i >= 1) v[x+i][y-i] = false; // 左下
    }
    return ;
}
void dfs(int row, vector<vector<bool>> table, vector<int>& nums) {
    if(row == n+1) {
        //只要三个输出，在没满三个之前输出，满了就只++
        if(ans < 3) {
            for(int i=1; i<=n; i++) cout << nums[i] << " ";
            cout << endl;
        }
        ans++;
        return;
    }

    for(int col=1; col<=n; col++) {
        if(table[row][col]) {
            vector<vector<bool>> new_table(table); //复制一份table方便修改和回溯
            nums[row] = col;         
            check(row, col, new_table); 
            dfs(row+1, new_table, nums); 
            //虽然没有明显的回溯，但是有实际上全都回溯了
            //nums[row] = 0;可以省略
        }
    }
}
int main() {
    cin >> n;
    vector<vector<bool>> table(n+1, vector<bool>(n+1, true));
    vector<int> nums(n+1, 0);  // 索引1-n

    //题目其实有隐藏的提醒，每一行只会有一个皇后存在，所以不需要遍历整个table
    //这个是个很大的优化，要不遍历整个table包超时的
    dfs(1, table, nums); 
    cout << ans;
    return 0;
}

那么看完上面我写的代码之后，是不是感觉自己完全ok了，实际上在佬看来还是有很大的优化空间的（因为我没有过全部样例）

那么接下来，我直接上剪枝优化

#include<bits/stdc++.h>
using namespace std;
int ans = 0;int n;
bool check(int x, int y, vector<int>& nums) {
    for (int i = 1; i < x; i++) {
        // 判断是否在同一列
        if (nums[i] == y) return false;
        // 判断是否在同一对角线，即两个坐标差值绝对值是否一样
        if (abs(nums[i] - y) == abs(i - x)) return false;
    }
    //没有判断是否在同一行，因为这个代码的逻辑就是每一行之存在一个
    return true;
}

void dfs(int row, vector<int>& nums) {
    if (row == n + 1) {
        // 只要三个输出，在没满三个之前输出，满了就只++
        if (ans < 3) {
            for (int i = 1; i <= n; i++) cout << nums[i] << " ";
            cout << endl;
        }
        ans++;
        return;
    }

    for (int col = 1; col <= n; col++) {
        // 因为删去了标记数组，没法简单粗暴的判定这个点是否可以放置皇后
        // 所以改变思路，判断当前位置在不在之前行的皇后可以吃掉的位置
        if (check(row, col, nums)) {
            // 不在之前所有皇后可以吃的地方
            nums[row] = col;
            dfs(row + 1, nums);
            nums[row] = 0;
            // 这个记得回溯啊
        }
    }
}

int main() {
    cin >> n;
    // vector<vector<bool>> table(n+1, vector<bool>(n+1, true)); 去除标记数组
    vector<int> nums(n + 1, 0);  // 索引1-n
    dfs(1, nums);
    cout << ans;
    return 0;
}//那么你看这个优化在了什么地方呢
//其一，去掉了table，是不是让dfs调用的时候更简单了
//其二，改变了for循环的判定，因为没有了table，使得无法通过棋盘判定是否可以放皇后
//所以我们改变check判定，减少多余的时间浪费
//提一个专业的，因为不需要更新table，直接的减少了时间复杂度，大概是从O(n多)变成了O(n)

还有更难的dfs，比如必须要剪枝才能执行，记忆化搜索（有点dp的感觉）

我还在网上看，有的老师会把dfs分成两类（递归dfs和用栈的dfs，但是我比较菜我看不懂）

附加图片和讲解视频地址

讲解视频源地址