#A. 毛毛虫树

Description

给你一棵树

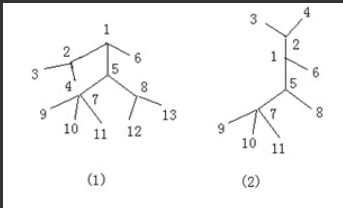
希望你找出一条链来，这条链上的点，及这些点直接相连的点，加起来点数尽可能的多

Format

Input

第一行两个整数N，M，分别表示树中结点个数和树的边数。

接下来M行，每行两个整数a, b表示点a和点 b有边连接（a, b≤N）。

你可以假定没有一对相同的(a, b)会出现一次以上。

N≤300000

Output

一个整数

Samples

输入数据 1

13 12

1 2

1 5

1 6

3 2

4 2

5 7

5 8

7 9

7 10

7 11

8 12

8 13

输出数据 1

11

---

思路

其实这道题是一个树形DP。

树的直径是求边权最大，本题求的则是点数最多,在求解之前，我们先做如下规定：

定义 dp[u]代表以u 的子树所能找到的 最长的“ 毛毛虫链"
定义 sz[u]为 u这个点的度数

分析可知以下几点:

1：如果u是叶子结点，则dp[u]=1;

2: 如果u不是叶子结点，并且整个树的“毛毛虫链”没有经过经点u的话,则点u的子节点对其父亲点u的贡献值分为3个部分：

第1部分为u的子结点v是贡献最大的一个，记为dp[v]；

第2部分为那些与u仅通过一条边相连的点的个数,也就是u的度数，记为sz[u]；

第3部分为u自己这个结点。

于是dp[u]=max(dp[v]+sz[u]+1-2,dp[u])，其中减去的２个点，一个为u的父亲点，一个为u所选中的那个子结点v。

如果整个树的“毛毛虫链”经过经点u，则形成的可行解统一为以u为根的子树中最长“毛毛虫链”加上“次长毛毛虫链”+sz[u]-1,此处并不需要对u是否为根结点进行特判，具体细节大家可自行推导一下。

---

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
int u,v,n,m,dp[10000001],ans;
vector<int> vec[10000001];
void dfs(int now,int fa) 
{
    dp[now] = 1;//初始化(如now为叶子结点,则没有子节点,也就是后面遍历now的所有子节点时dp[now]不会变化)
    int l = vec[now].size(),mx1 = 0,mx2 = 0;
//l:与now距离为1的节点数量,也就是now的度,相当与上面所讲的sz[now]
//mx1:最长链,相当与上面所讲的dp[v]   mx2:次长链
    for(int i = 0; i < l; i++) 
    {
        int t = vec[now][i];
        if(t == fa) continue;//因为now的父节点与now距离为也为1,可我们要遍历的只是now的子节点
        dfs(t,now);
        int k = dp[t];
        if(k > mx1) swap(mx1,k);
        if(k > mx2) swap(mx2,k);
        dp[now] = max(dp[now],mx1 + l - 1);//套用"dp[u]= max(dp[u],dp[v]+sz[u]+1-2)"的公式
    }
    ans = max(ans,mx1 + mx2 + l - 1);
//套用上面所讲的"以u为根的子树中最长“毛毛虫链”加上“次长毛毛虫链”+sz[u]-1"的公式
}
signed main() 
{
    cin>>n>>m;
    while(m--) 
    {
        cin>>u>>v;
        vec[u].push_back(v);//建无向图
        vec[v].push_back(u);
    }
    dfs(1,0);
    cout<<ans;
    return 0;
}