【JZOJ5330】密码
(File IO): input:password.in output:password.out
Time Limits: 1000 ms Memory Limits: 262144 KB
Description

Input

Output

Sample Input
4 2 2
Sample Output
2
Data Constraint

Hint
样例解释
解题思路
看到 pk|Csl(p是质数) 这种东西,立刻想到库默尔定理
库默尔定理
Theorem:
设m,n为正整数,p为素数,则 Cmm+n 含p的幂次等于m+n在p进制下的进位次数。
反过来
Cmn
含p的幂次等于m-n在p进制下的退位次数。
定理证明:
设
f(n,p)
表示n含p的幂次,有
f(n!,p)=∑∞i⌊npi⌋
那么
∵Cnm=m!n!(m−n)!∴f(Cnm,p)=f(m!,p)−f(n!,p)−f((m−n)!,p)
∴f(Cnm,p)=∑i∞⌊mpi⌋−⌊npi⌋−⌊m−npi⌋
⌊mpi⌋−⌊npi⌋−⌊m−npi⌋ 的取值只可能是{0,1},而且当且仅当m-n在p进制下第i位退位时,它的值为1。
所以 Cmn 含p的幂次等于m-n在p进制下的退位次数。
原命题得证!
回到题目,我们只要统计出所有l-s在p进制下退位次数不小于k的组数
考虑从低位到高位转移数位DP:
设
fi,j,0/1,0/1
表示,在p进制下做到第i位,退位次数为j,i位其后的数是否大于上界的后i位,是否退位
转移方程自己推推就好了,几个等差数列而已。
#include<cstring>
#include<cstdio>
#include<cctype>
#include<algorithm>
#define mo 1000000007
using namespace std;
typedef long long ll;
const int N=3333;
int f[N][N][2][2],k;
ll t[1001],n[N],ans,p;
int main(){
freopen("password.in","r",stdin);
freopen("password.out","w",stdout);
for(char c;(c=getchar())>='0' && c<='9';)t[++t[0]]=c-'0';scanf("%lld %d",&p,&k);
for(int i=1;i+i<=t[0];i++)swap(t[i],t[t[0]+1-i]);
while(t[0]){
for(int i=t[0];i;i--){
if(i>1)t[i-1]+=t[i]%p*10;else n[++n[0]]=t[i]%p;t[i]/=p;
}while(t[0] && !t[t[0]])t[0]--;
}if(n[0]<k){printf("0");return 0;}
f[0][0][0][0]=1;
for(int i=0;i<n[0];i++)for(int j=0;j<=i;j++){
f[i+1][j][0][0]=((ll)f[i+1][j][0][0]+(n[i+1]+1)*(n[i+1]+2)/2%mo*(ll)f[i][j][0][0]+n[i+1]*(n[i+1]+1)/2%mo*((ll)f[i][j][0][1]+(ll)f[i][j][1][0])+n[i+1]*(n[i+1]-1)/2%mo*(ll)f[i][j][1][1])%mo;
f[i+1][j+1][0][1]=((ll)f[i+1][j+1][0][1]+(2*p-n[i+1]-2)*(n[i+1]+1)/2%mo*(ll)f[i][j][0][0]+(2*p-n[i+1])*(n[i+1]+1)/2%mo*(ll)f[i][j][0][1]+(2*p-n[i+1]-1)*n[i+1]/2%mo*(ll)f[i][j][1][0]+(2*p-n[i+1]+1)*n[i+1]/2%mo*(ll)f[i][j][1][1])%mo;
f[i+1][j][1][0]=((ll)f[i+1][j][1][0]+(n[i+1]+p+2)*(p-n[i+1]-1)/2%mo*(ll)f[i][j][0][0]+(p+n[i+1])*(p-n[i+1]-1)/2%mo*(ll)f[i][j][0][1]+(p+n[i+1]+1)*(p-n[i+1])/2%mo*(ll)f[i][j][1][0]+(p+n[i+1]-1)*(p-n[i+1])/2%mo*(ll)f[i][j][1][1])%mo;
f[i+1][j+1][1][1]=((ll)f[i+1][j+1][1][1]+(p-n[i+1]-2)*(p-n[i+1]-1)/2%mo*(ll)f[i][j][0][0]+(p-n[i+1])*(p-n[i+1]-1)/2%mo*((ll)f[i][j][0][1]+(ll)f[i][j][1][0])+(p-n[i+1]+1)*(p-n[i+1])/2%mo*(ll)f[i][j][1][1])%mo;
}
for(int i=k;i<=n[0];i++)ans=ans+f[n[0]][i][0][0];printf("%lld",ans%mo);
fclose(stdin);fclose(stdout);
return 0;
}










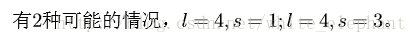














 2450
2450

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








