QR分解：Householder 变换原理与代码设计

Householder 变换

---

反射矩阵

对任意模为1的向量$u\in R$,有矩阵$H=I-2u{u}^T$,并满足：

• $H=H^T$
• $H\ast H=I$

简单证明：

• $H^T=(I-2u{u}^T{)}^T=I-2(u^T{)}^T{u}^T=I-2u{u}^T=H$
• $H\ast H=(I-2u{u}^T)\ast (I-2u{u}^T)=I-4u{u}^T+4u(u^{T}u)u^T=I$

记超平面$S$（过原点以$u$为法向）：
S = { x ∣ u T x = 0 , ∀ x ∈ R n } S=\{x|u^Tx=0,\forall x \in R^n\} S={x∣uTx=0,∀x∈Rn}
任一向量$z\in R^n$可以在子空间$S$和 s p a n { u } span\{u\} span{u}做正交分解：
$$z=x+y,x\in S,y\in \alpha \cdot u,\alpha \in R$$
将矩阵$H$作用到$z$上，于是：
$$\begin{array}{rl}Hz& =Hx+Hy\\ & =(I-2u{u}^T)x+(I-2u{u}^T)y\\ & =x+y-2u{u}^{T}y\\ & =x+y-2\alpha u(u^{T}u)\\ & =x-y\end{array}$$
通过矩阵$H$的变换，将$x+y$以$S$为镜面反射到$x-y$ ，因此矩阵$H$叫做反射矩阵，而这一变换过程叫做Householder变换。

---

上三角化处理

定理：给定两个模长相等的向量$x,y\in R$，则存在反射变幻$H$，使$Hx=y$

对$\forall x\in R^n,||x||=\rho$，可以通过Householder变幻H得到：
$$Hx=[\pm \rho ,0,...,0{]}^T$$
构建反射矩阵H时，需满足$u$的模为1，因此取：
$$u=\frac{x-y}{||x-y||}$$
对于给定方阵，可通过反射变幻逐列进行上三角化操作：
$$\left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\stackrel{H_1=I-2u_1{u}_1^T}{⟶}\left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ 0& \ast & \ast & \ast \\ 0& \ast & \ast & \ast \\ 0& \ast & \ast & \ast \end{array}\right]\stackrel{H_2=I-2u_2{u}_2^T}{⟶}\left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ 0& \ast & \ast & \ast \\ 0& 0& \ast & \ast \\ 0& 0& \ast & \ast \end{array}\right]\stackrel{H_3=I-2u_3{u}_3^T}{⟶}\left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ 0& \ast & \ast & \ast \\ 0& 0& \ast & \ast \\ 0& 0& 0& \ast \end{array}\right]$$
通过一系列$H$作用到$A$，可将其逐渐化为上三角矩阵，于是上述过程可描述为：
$$H_{n-1}{H}_2{H}_1\cdot A=R,PA=R,A=P^{T}R=QR$$
注：这里的$H_n$实际上为$diag(I,H_n)$,仅为表达公式的合理性。在实际代码实现过程中，我们并不会将其补全再计算。

逐列上三角化操作流程

例如，对于$m\times n$维矩阵$A_{m\times n}(m\ge n)$进行上三角化操作，从第一列$A_1=[a_{11}{a}_{21}\cdots a_{m1}{]}^T$开始：

• 计算$\rho =-sgn(a_{11})\stackrel{m}{\sum _{i=1}}{a}_{i1}$，其中$sgn$为取符号操作，$-sgn(a_{11})$是为了保证$|u_1|=|a_{11}-\rho |$尽可能地大，避免数值精度损失，于是变换后的${\hat{A}}_1=[\rho ,0,\dots ,0{]}^T$。

• 计算$u_1$（$x-y$），由式（5）可知，这里$x$指的是变换前的$A_1=[a_{11}{a}_{21}\cdots a_{m1}{]}^T$，$y$指的是变换后的${\hat{A}}_1=[\rho ,0,\dots ,0{]}^T$。显然，$u_1(1)=a_{11}-\rho ,u(n)=A_1(n),n>1$

• 计算缩放因子${\beta }_1$，${\beta }_1=||x-y||=||u||=\frac{-1}{\rho u_1(1)}$

于是：
$$T_{u_1}{A}_1=[\rho ,0,\dots ,0{]}^T$$
上述公式即完成了对第一列元素的更新，主对角线元素以下皆为0。对于第$2,3,\dots ,n$列元素的更新，可按照下式进行：
$$T_{u_j}{A}_j=A_j-\beta (A_j^{T}u)u$$
当n列元素均更新完毕后，至此，$H_1\cdot A=R_1$已计算完毕，已完成等式（6）中第一步至第二步的转化。仿照上述步骤，逐列对矩阵$A_{m\times n}$进行上三角化操作。当矩阵加入新的参数时，为了避免重复计算，需要记录$u_1,u2,\dots ,u_n$和${\beta }_1,{\beta }_2,\dots ,{\beta }_n$。

---

C语言代码实现

仿照上述公式实现下C语言代码，在工程应用中，为了节省空间，可以将需要记录的$u_1,u2,\dots ,u_n$和${\beta }_1,{\beta }_2,\dots ,{\beta }_n$记录在上三角化之后的矩阵中。若是如此，则需要确保矩阵空间开辟时，行数要增加2。

例如：对矩阵$A_{4\times 4}$进行上三角化操作（实际开辟维度为$6\times 4$），当第一列完成上三角化后：
$$\left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\stackrel{H_1=I-2u_1{u}_1^T}{⟶}\left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ 0& \ast & \ast & \ast \\ 0& \ast & \ast & \ast \\ 0& \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \\ \ast & \ast & \ast & \ast \end{array}\right]\stackrel{A_{i1}=u_i,(i>1)}{⟶}\left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ u_1& \ast & \ast & \ast \\ u_2& \ast & \ast & \ast \\ u_3& \ast & \ast & \ast \\ u_4& \ast & \ast & \ast \\ {\beta }_1& \ast & \ast & \ast \end{array}\right]$$
当所有列均上三角完成后，矩阵A为：
$$\left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ u_{11}& \ast & \ast & \ast \\ u_{12}& u_{21}& \ast & \ast \\ u_{13}& u_{22}& u_{31}& \ast \\ u_{14}& u_{23}& u_{32}& u_{41}\\ {\beta }_1& {\beta }_2& {\beta }_3& {\beta }_4\end{array}\right]$$

在实际工程计算中，后续继续增加待定参数时，无需重复计算$u$和$\beta$，提高计算效率。

---

具体代码实现如下：

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h>

#define MAX 1024
#define ROW 4
#define COL 4

// 返回x的绝对值，y的符号
double sign(double x, double y)
{
    return fabs(x) * (y >= 0 ? 1 : -1);
}
// 获取每列元素，u,s,beta
void get_ele(double **src, int n, int row, double u[], double *s, double *beta)
{
    int i, j;
    double s1;
    *beta = *s = s1 = 0.0;
    for (i = n; i < row; i++)
    {
        s1 += src[i][n] * src[i][n];
    }
    s1 = -sqrt(s1) * sign(1, src[n][n]);
    if (s1 == 0.0)
    {
        printf("*****WARRING(get_ele):s equal 0.0, column: %d\n", n + 1);
        return;
    }
    u[0] = src[n][n] - s1;
    if (u[0] == 0.0)
    {
        printf("*****WARRING(get_ele):u[0] equal 0.0, column: %d\n", n + 1);
        return;
    }
    for (i = 1; i < row - n; i++)
    {
        u[i] = src[n + i][n];
    }
    *beta = 1.0 / s1 / u[0];
    *s = s1;
}
// householder变换
void householder(double **src, int row, int col, bool save)
{
    int i, j, k, flag = 1, tmp;
    double s, beta, gama;
    double u[MAX] = {0};

    if (src == NULL)
    {
        printf("*****ERROR(householder):src Matrix is NULL, exit!\n");
        exit(-1);
    }
    for (i = 0; i < col; i++)
    {
        // check elemental first
        flag = 1;
        tmp = 0;
        for (j = i + 1; j < row; j++)
        {
            if (src[j][i] == 0)
            {
                tmp++;
            }
        }
        if (tmp == row)
        {
            flag = 0;
            if (save)
            {
                src[j + 1][i] = 0;
                src[j = 2][i] = 0;
            }
        }
        if (flag)
        {
            get_ele(src, i, col, u, &s, &beta);
            if (s == 0.0)
                continue;
            src[i][i] = s;
            for (j = i + 1; j < col; j++)
            {
                gama = 0.0;
                for (k = i; k < row; k++)
                {
                    gama += u[k - i] * src[k][j];
                }
                if (gama == 0.0)
                    continue;
                gama *= beta;
                for (k = i; k < row; k++)
                {
                    src[k][j] += gama * u[k - i];
                }
            }
        }
        if (save)
        {
            for (j = i + 1; j < row + 1; j++)
            {
                src[j][i] = u[j - i - 1];
            }
            src[j][i] = beta;
        }
        else
        {
            for (j = i + 1; j < row; j++)
            {
                src[j][i] = 0.0;
            }
        }
    }
}

---

测试用例：

void test1(bool save)
{
    int i, j;
    double **arr = (double **)malloc(sizeof(double *) * (ROW + 2));
    for (i = 0; i < ROW + 2; i++)
    {
        arr[i] = (double *)malloc(sizeof(double) * COL);
        memset(arr[i], 0, sizeof(double) * COL);
    }
    arr[0][0] = 1;
    arr[1][0] = 1;
    arr[2][0] = 1;
    arr[3][0] = 1;

    arr[0][1] = 2;
    arr[1][1] = 0;
    arr[2][1] = 0;
    arr[3][1] = 2;

    arr[0][2] = 0;
    arr[1][2] = 3;
    arr[2][2] = 3;
    arr[3][2] = 0;

    arr[0][3] = 1;
    arr[1][3] = 1;
    arr[2][3] = 2;
    arr[3][3] = 2;

    householder(arr, ROW, COL, save);
	
    
    for (i = 0; i < ROW + 2; i++)
    {
        for (j = 0; j < COL; j++)
        {
            printf("%5.2lf  ", arr[i][j]);
        }
        putchar('\n');
    }
}

int main(int argc, char *argv[])
{
    test1(false);
    test1(true);
    return 0;
}

---

结果：

第一种情况为不存储$u,\beta$，第二种情况则为存储，根据具体需求进行选择。

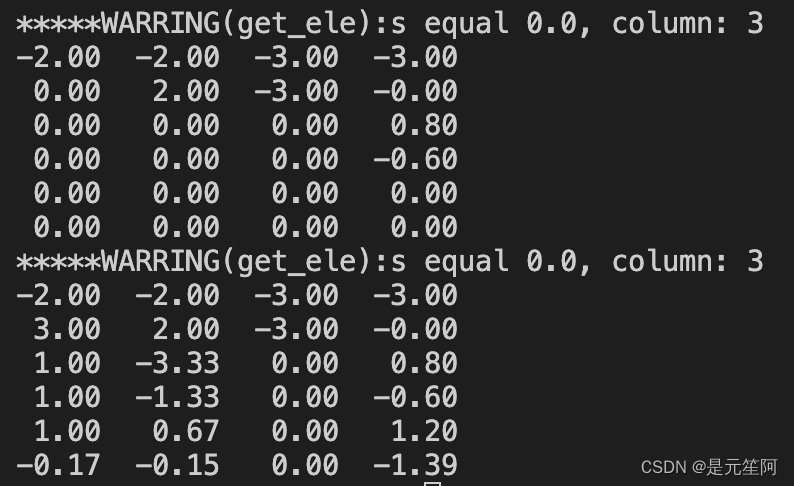
注意：

• s的计算策略不同（s1=sqrt(s1)或者 s1 = -sqrt(s1) * sign(1, src[n][n]) ），最后展示结果略有差异，后者稳定性更佳，通过矩阵的基本原理可知，这几种结果均是等价的
• 实际工程计算中，s为0时将会影响后续对矩阵进行求逆，需要谨慎