计算卫星高度角、方位角（XYZ转ENU，ENU转RAH）

    最小二乘定权、电离层对流层改正，都需要卫星的高度角、方位角。本章将介绍求解完卫星的地固坐标系的位置后，如何求解卫星的高度角、方位角。

    卫星位置求解请参考之前的博客：卫星位置解算原理与程序设计

   

参考书籍：黄丁发，熊永良，周乐韬等，GPS卫星导航定位技术与方法，科学出版社。

本文内容较适合初学者进行学习，如若需要更高精度的计算，请移步至RTKLIB函数专栏，有详细介绍。

更新：修改了文章中笔误情况，对代码进行了优化，加强了整体逻辑。

---

目录

公式原理

程序设计（C语言）

结构体定义：

xyz转blh：

xyz转enu：

求卫星方位角、高度角 

---

主要步骤： 

        1）欧拉角旋转的方法将卫星的xyz坐标转换为站心坐标系的enu坐标（求解ENU需要BLH）

        2）然后通过高度角和方位角公式计算卫星在站心坐标系中的高度角和方位角。

---

公式原理

    站心坐标系也称NEU坐标系或东北高坐标系，在地球上任一点观测卫星时，最直观和最方便的办法是知道卫星所在的瞬时位置的方位和仰角。因此，需将卫星的地固坐标系转化成站心坐标系。 

    站心直角坐标系是以测站为坐标原点的左手坐标系，其N轴指向过该测站的子午线，北向为正；U轴重合与该点上WGS84椭球法线，向外为正；E轴位于该点的切平面，东向为正，如下图所示： 

站心直角坐标系

     站心坐标系常用极坐标表示（方位角A、高度角h、向径r），如下图所示：

站心极坐标系
​​​​

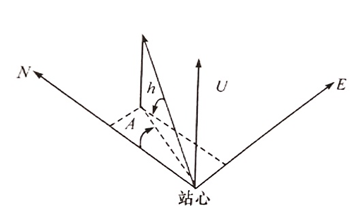
    建立以已知测站点为原点的站心直角坐标系，则卫星在该坐标系的坐标XL(E、N、U)为：

式中：为卫星在地固系中的坐标向量；为测站在地固坐标系中的坐标向量；为卫星在站心坐标系中的坐标向量；R为旋转矩阵，即： 

 式中：B,L为测站的大地维度和大地精度。

    卫星从站心直角坐标系转换到站心极坐标系的公式为：

式中：r为卫星向径，A为卫星方位角，h为卫星的高度角。

---

程序设计（C语言）

整体流程为：

1）通过测站XYZ求出其经纬度

2）通过测站经维度与测站和卫星的三维坐标差，求出卫星以测站为原点的ENU坐标

3）通过ENU，计算卫星的方位角与高度角

下面代码，XYZ单位均为米，角度单位均为弧度制，Xr，Yr，Zr表示参考点（测站）的三维坐标，Xs，Ys，Zs表示卫星的三维坐标。

结构体定义：

#include <stdio.h>
#include <math.h>
typedef struct BLH
{
	double B;
	double L;
	double H;
} BLH, *pBLH;

typedef struct ENU
{
	double E;
	double N;
	double U;
} ENU, *pENU;

typedef struct RAH
{
    double R;
    double A;
    double H;
} RAH, *pRHA;

xyz转blh：

xyz转blh的原理与程序设计思路请见：xyz转BLH

BLH xyz2blh(double X, double Y, double Z)
{
	double a,f,e2,B = 0.0, N = 0.0, H = 0.0, R0, R1, deltaH, deltaB;;
	a=6378137.0,f=(1.0 / 298.257223563),e2=f*(2-f);
	BLH res = { 0 };
	R0 = sqrt(pow(X, 2) + pow(Y, 2));
	R1 = sqrt(pow(X, 2) + pow(Y, 2) + pow(Z, 2));
	//经度直接求解
	res.L = atan2(Y, X);
	//迭代求大地维度和大地高
	N = a;
	H = R1 - a;
	B = atan2(Z * (N + H), R0 * (N * (1 - e2) + H));
	do
	{
		deltaH = N;//判断收敛所用
		deltaB = B;
		N = a / sqrt(1 - e2 * pow(sin(B), 2));
		H = R0 / cos(B) - N;
		B = atan2(Z * (N + H), R0 * (N * (1 - e2) + H));
	} while (fabs(deltaH - H) > 1.0e-3 && fabs(deltaB - B) > 1.0e-9);
	res.B = B;
	res.H = H;
	return res;
}

xyz转enu：

ENU xyz2enu(double Xr, double Yr, double Zr, double Xs, double Ys, double Zs)
{
    ENU enu = { 0 };
    BLH ref = xyz2blh(Xr, Yr, Zr);
    double sinL = sin(ref.L);
    double cosL = cos(ref.L);
    double sinB = sin(ref.B);
    double cosB = cos(ref.B);
    double dx = Xs - Xr;
    double dy = Ys - Yr;
    double dz = Zs - Zr;
    enu.E = -sinL*dx + cosL*dy;
    enu.N = -sinB*cosL*dx - sinB*sinL*dy + cosB*dz;
    enu.U = cosB*cosL*dx + cosB*sinL*dy + sinB*dz;
    return enu;
}

求卫星方位角、高度角 

RAH Satrah(double Xr, double Yr, double Zr, double Xs, double Ys, double Zs)
{
    RAH rah = {0};
    ENU enu = xyz2enu(Xr, Yr, Zr, Xs, Ys, Zs);
    rah.H = atan2(enu.U, sqrt(enu.E * enu.E + enu.N * enu.N));
    rah.A = atan2(enu.E, enu.N);
    if (rah.A < 0)
        rah.A += 2 * PI;
    if (rah.A > 2 * PI)
        rah.A -= 2 * PI;
    rah.R = sqrt(enu.E * enu.E + enu.N * enu.N + enu.U * enu.U);
    return rah;
}

1）atan2为四象限反正切函数（atan，atan2并不相同），三角函数单位均为弧度

2）方位角A范围在0~360°；若A＜0，A=A+2pi；若A＞2pi，A=A-2pi

3）atan2的范围为-90°～90°，高度角的范围在0～90°，RTKLIB中保留了高度角的符号，因此无需对高度角再进行归化。

3）本次演示代码为使逻辑更加清晰，采取传入形参，以结构体作为返回值，也可以直接传入指针，通过指针修改更加便捷。

4）计算BLH时，大地高未加入地球曲率改正，若对大地高有精度要求，请移步至RTKLIB函数专栏，里面有详细介绍。