本文将给大家介绍一下如何利用矩阵分解来做推荐系统算法。矩阵分解是指把一个矩阵分解成若干个矩阵的某种运算的合成,一般见得比较多的是相乘,本文给大家的介绍的也是相乘。一个比较著名的矩阵分解算法是SVD,SVD是将已有的评分矩阵分解为3个矩阵,有了这3个矩阵,就可以预测用户对某个未评分item的分值,一般将原始的评分矩阵分解成这3个矩阵之后,会做一定的降维处理,之后再做预测。利用SVD做推荐已经取得了良的效果,但是由于进行SVD计算时,不能有缺失值,如果要用SVD,则必须先填补缺失值,如果全填为0,则表示用户打了0分,显然不合理,填为其它值如随机值等也不合适。
那么有没有一种方法能只考虑评过分的item而不考虑缺失评分的item?有,这里给大家介绍一种用类似SVD的方法将矩阵分解为两个矩阵相乘,并且只考虑有评论的项,训练时可以不考虑缺失项。
首先将 user 对 item 的评分表示为矩阵,如原始的评分矩阵:
将该矩阵分解为两个矩阵相乘:
其中左边矩阵的非空元素为





当分解成了Q和P两个矩阵后,空白处的值就可以通过Q矩阵的某列和P矩阵的某列相乘,得到缺失处的值。这背后的核心思想,简单说就是,找到两个矩阵,它们相乘之后得到的那个矩阵的值,和待分解矩阵中有值的位置中的值尽可能地接近,这样以来,分解出来的两个矩阵相乘就尽可能地还原了待分解矩阵,因为有值的地方,值都相差得尽可能地小,那么没有值的地方,通过这样的方式算出的值,也就比较符合趋势,毕竟矩阵尽可能地接近了有值的位置上的值。
那么,我们如何求得那两个矩阵呢,可以用很容易地用gradient descent求得,首先写出 cost function:
第一项就是误差项,就是用原评分矩阵中有值的项,减去Q和P对应行、列相应后得到的值,第二项是正则化项,防止过拟合。那么最小化 cost function 就求出了P和Q:
用gradient descent求解P和Q,求梯度步骤很简单,就省略了。现在给出update rules,对每一个原矩阵中有值的项:
多次迭代之收敛后就求出了矩阵P和Q。
上面是将评分矩阵仅仅分解成两个矩阵相乘,这是最简单的形式,除了这种简单的形式,还可以加一些其它的约束以改善推荐的效果,例如分解成下列形式:

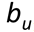


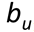

下面给大家介绍一篇paper,An Experimental Study on Implicit SocialRecommendation (SIGIR2013),这篇paper是研究用矩阵分解的方法做推荐系统。上面说到,除了将评分矩阵仅仅分解成两个矩阵相乘之外,还可以加一些其它约束,这些约束一般是以正则化项的形式出现在cost function中,下面给出这篇paper中cost function:
其中

第1,4,5项比较好理解,就是之前介绍的最简单的那种形式,第2,3项是作者提出的user之间的隐含关系以及item之间的隐含关系考虑进去所定义出来的项,其中

user i 和 user f 之间的皮尔森相关系数:
item j 和 item q 之间的皮尔森相关系数:
paper里做了一个小的处理,对于最不相似的那些user和item,把相似度取了相反数,以便和相似用户放在一起统一训练。 这样一来,cost function 中第2,3项的作用就在于,希望两个similarity高的user,它们对应的u向量接近,同样希望两个similarity高的item,它们对应的v向量接近。这个应该很好理解,比如说,有两个user它们的similarity很高,但这两个user对应的u向量相差得很大,那么cost function中的这项
好了,这下就能求出矩阵U和V啦,那怎么检验训练出来的model是好是坏呢?那就要用一些trainingset之外的评分数据来检验,就是在训练的时候,给矩阵保留了一些值不参与训练,在训练完成后,用矩阵U和V计算出原分矩阵中的那些保留值的值对应位置的值,跟原来保留的值比较,看看误差是多少,一般常用均方根误差(RMSE)来衡量:
参考:
An Experimental Study on Implicit SocialRecommendation (SIGIR2013)
Stanford CS246 课程 PPT

































 382
382











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








