案例系列：银行个人贷款营销_预测客户是否购买贷款_多个分类模型比较

银行个人贷款营销_预测客户是否购买贷款_多个分类模型比较

链接

数据链接
https://www.kaggle.com/datasets/itsmesunil/bank-loan-modelling/

代码链接
https://download.csdn.net/download/wjjc1017/88640155

介绍

在这个项目中，我们将解决一个关于对Thera-Bank数据集进行个人贷款分类的问题。Thera-Bank的大部分客户都是存款人。同时也是借款人（资产客户）的客户数量相当少，银行有兴趣快速扩大这一客户群体，通过贷款利息来增加收入。特别是，管理层希望寻找方法将其负债客户转化为零售贷款客户，同时保持他们作为存款人。去年银行针对存款客户进行的一项活动显示了超过9.6%的转化率成功。这促使零售营销部门开发了更好的目标营销活动，以提高成功率并减少预算开支。该部门希望开发一个分类器，帮助他们识别更有可能购买贷款的潜在客户。这将提高成功率同时降低活动成本。

数据集包含客户信息和客户对上次个人贷款活动的响应：

• ID：客户的ID

• Age：客户的年龄（以完整的年份计算）

• Experience：工作经验年限

• Income：年收入金额（以千为单位）

• Zipcode：客户所在的邮政编码

• Family：家庭成员数量

• CCAvg：信用卡的平均月度消费金额（以千为单位）

• Education：教育水平（1：学士学位，2：硕士学位，3：高级/专业学位）

• Mortgage：房屋抵押价值（如果有的话，以千为单位）

• Securities Account：客户是否在该银行拥有证券账户？

• CD Account：客户是否在该银行拥有定期存款账户（CD）？

• Online：客户是否使用网上银行服务？

• CreditCard：客户是否使用该银行发行的信用卡？

• Personal Loan：该客户是否接受了上次活动中提供的个人贷款？（目标变量）

目标： 使用不同的分类模型预测客户购买个人贷款的可能性。

让我们开始吧：

步骤1：导入库

# 导入所需的库

import numpy as np
import pandas as pd
import pandas_profiling
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
from matplotlib.colors import ListedColormap, LinearSegmentedColormap
from sklearn.model_selection import train_test_split, GridSearchCV, StratifiedKFold, cross_val_score
from sklearn.preprocessing import KBinsDiscretizer, OneHotEncoder, StandardScaler
from sklearn.naive_bayes import ComplementNB, BernoulliNB
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from sklearn.ensemble import AdaBoostClassifier, GradientBoostingClassifier
from xgboost import XGBClassifier
from sklearn.pipeline import Pipeline
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score, roc_auc_score
from sklearn.metrics import classification_report, RocCurveDisplay, ConfusionMatrixDisplay
from scipy import stats
from sklearn.base import clone 
%matplotlib inline

# 以上是导入所需的库，这些库包含了数据处理、可视化、模型训练和评估等功能。

# 以下是代码的具体实现部分，具体实现了数据预处理、模型训练和评估等功能。

第二步：读取数据集

# 读取Excel文件中的数据，并将数据存储在DataFrame中
df = pd.read_excel('/kaggle/input/bank-loan-modelling/Bank_Personal_Loan_Modelling.xlsx', sheet_name='Data')

# 显示DataFrame的前5行数据
df.head(5)

	ID	Age	Experience	Income	ZIP Code	Family	CCAvg	Education	Mortgage	Personal Loan	Securities Account	CD Account	Online	CreditCard
0	1	25	1	49	91107	4	1.6	1	0	0	1	0	0	0
1	2	45	19	34	90089	3	1.5	1	0	0	1	0	0	0
2	3	39	15	11	94720	1	1.0	1	0	0	0	0	0	0
3	4	35	9	100	94112	1	2.7	2	0	0	0	0	0	0
4	5	35	8	45	91330	4	1.0	2	0	0	0	0	0	1

步骤3：数据集单变量分析

为了更精确地检查数据集，我们使用 pandas_profiling 进行单变量分析。它通过 df.profile_report() 扩展了 pandas dataframe，以便进行快速数据分析：

# 使用pandas_profiling生成数据集的报告
df.profile_report()

Summarize dataset:   0%|          | 0/5 [00:00<?, ?it/s]



Generate report structure:   0%|          | 0/1 [00:00<?, ?it/s]



Render HTML:   0%|          | 0/1 [00:00<?, ?it/s]

**____________________________________________

数据集基本信息：

• 数据集中有5000个客户。
• 我们有14个变量，包括13个自变量和1个因变量，即个人贷款。
• 我们有6个数值变量：ID，年龄，经验，收入，信用卡平均消费，抵押贷款
• 我们有3个分类变量：家庭，教育，邮编
• 我们有5个布尔变量：个人贷款，证券账户，存款账户，网上银行，信用卡
• 数据集中没有缺失值。
• 数据集中没有重复值。
• 数据集中的经验存在负值，这是不合理的。
• ID均匀分布。因此，ID作为标识符，对模型缺乏有价值的信息。
• 邮编包含大量类别（467个类别）。因此，它似乎对我们的模型缺乏很多信息。

分类变量分析：

• 教育 - 42%的候选人拥有学士学位，30%拥有硕士学位，28%是专业人士。
• 家庭 - 约29%的客户家庭规模为1人，26%为2人，20%为3人，24%为4人。

布尔变量分析：

• 个人贷款 - 上次活动中约90%的客户没有接受个人贷款。数据集不平衡！
• 存款账户 - 94%的客户没有与该银行开设存款账户。
• 信用卡 - 约71%的客户不使用信用卡。
• 网上银行 - 约60%的客户使用网上银行服务。
• 证券账户 - 约90%的客户没有与该银行开设证券账户。

数值变量分析：

• 年龄 - 客户的平均年龄为45岁，标准差为11.5。直方图曲线相对对称。
• 信用卡平均消费 - 每月信用卡平均消费的平均值为1.94，标准差为1.75。曲线高度正偏斜。
• 收入 - 客户的平均年收入为73.77，标准差为46。曲线中度正偏斜。
• 抵押贷款 - 房屋抵押贷款的平均值为56.5，标准差为101.71！曲线高度正偏斜（偏度=2.1），有很多异常值（峰度=4.76）

可以看出，ID具有均匀分布。ID的值都是唯一的，实际上ID作为标识符，对模型缺乏有价值的信息。因此，我们将删除此特征：

# 删除数据框df中的'ID'列，axis=1表示按列删除，inplace=True表示在原数据框上进行修改

步骤4：相关性分析

让我们比较一下Spearman的相关性和Pearson的相关性：

• Pearson适用于两个变量之间的线性关系，而Spearman适用于单调关系。
• Pearson使用变量的原始数据值，而Spearman使用排名顺序的变量。

当变量之间存在“可能是单调的，可能是线性的”关系时，我们最好使用Spearman而不是Pearson：

# 导入需要的模块
from matplotlib.colors import LinearSegmentedColormap

# 定义一个名为"royalblue"的线性分段颜色映射
# 该颜色映射由两个颜色组成，分别是白色和深蓝色
royalblue = LinearSegmentedColormap.from_list('royalblue', [(0, (1,1,1)), (1, (0.25,0.41,0.88))])

# 创建一个反转的"royalblue"颜色映射
royalblue_r = royalblue.reversed()

# 导入必要的库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 计算Spearman相关系数
target = 'Personal Loan'  # 目标变量为'Personal Loan'
df_ordered = pd.concat([df.drop(target,axis=1), df[target]],axis=1)  # 将目标变量放在数据框的最后一列
corr = df_ordered.corr(method='spearman')  # 计算相关系数矩阵，使用Spearman方法

# 创建一个掩码，以便只显示相关系数值一次
mask = np.zeros_like(corr)  # 创建一个与相关系数矩阵大小相同的全零矩阵
mask[np.triu_indices_from(mask,1)] = True  # 将矩阵的上三角部分设为True，下三角部分设为False

# 绘制热力图
plt.figure(figsize=(12,8), dpi=80)  # 设置图形大小
sns.heatmap(corr, mask=mask, annot=True, cmap=royalblue, fmt='.2f', linewidths=0.2)  # 绘制热力图，使用掩码显示相关系数，显示数值，使用royalblue颜色映射，保留两位小数，设置边框宽度为0.2
plt.show()  # 显示图形

结论：

• 个人贷款 与 收入、CD账户、平均信用卡支出 高度相关。
• 经验 与 年龄 高度相关。 (ρ = 0.99)
• 平均信用卡支出 与 收入 有较高的相关性。 (ρ = 0.58)

步骤 5：数据清洗

数据清洗，也被称为数据清理，是将原始数据准备和结构化的过程，以便用于进一步的分析。它包括识别和纠正不正确或不完整的数据，删除无关的数据，填补缺失值，并转换现有变量。数据清洗是任何机器学习项目中的重要步骤，因为它通过减少噪声和错误来提高模型的准确性。清洗不好的数据可能导致过于复杂的模型，难以解释，并且有很高的过拟合风险。此外，脏数据可能会显著降低模型的准确性；即使有少量噪声，也会大大降低其性能。

步骤 5.1：噪声处理

噪声处理 是在数据用于分析之前，将无关或嘈杂的部分从数据集中移除的过程。

I) 邮政编码噪声处理：

在第3步中，我们发现邮政编码特征的最小值远小于平均值。让我们再次查看该特征的直方图：

# 设置图形的样式为darkgrid
sns.set_style('darkgrid')

# 设置颜色为royalblue
color = 'royalblue'

# 创建一个图形对象，设置图形的大小和分辨率
plt.figure(figsize=(15,5), dpi=120)

# 绘制直方图，x轴为'ZIP Code'列的数据，数据来源为df，设置bin的数量为60，颜色为color
graph = sns.histplot(x='ZIP Code', data=df, bins=60, color=color)

# 显示每个柱状图的非零值
labels = [str(v) if v else '' for v in graph.containers[0].datavalues]
graph.bar_label(graph.containers[0], labels=labels)

# 添加一个注释，注释内容为'Noise'，注释的位置为(10000,60)，注释文本的位置为(12000,400)，颜色为color，字体大小为15
plt.annotate('Noise', xy=(10000,60), xytext=(12000,400), color=color, fontsize=15, 
             arrowprops=dict(facecolor=color, shrink=0.01))

# 设置x轴标签为'ZIP Code'，字体大小为15
plt.xlabel('ZIP Code', fontsize=15)

# 设置y轴标签为'Count'，字体大小为15
plt.ylabel('Count', fontsize=15)

# 设置图形的标题为'ZIP Code Distribution'，字体大小为20
plt.suptitle('ZIP Code Distribution', fontsize=20)

# 调整图形的布局
plt.tight_layout()

# 显示图形
plt.show()

# 读取数据文件，并将其存储在名为df的数据框中
df = pd.read_csv('data.csv')

# 通过筛选条件，选取'ZIP Code'列中小于20000的行，并将结果存储在新的数据框中
filtered_df = df[df['ZIP Code'] < 20000]

	Age	Experience	Income	ZIP Code	Family	CCAvg	Education	Mortgage	Personal Loan	Securities Account	CD Account	Online	CreditCard
384	51	25	21	9307	4	0.6	3	0	0	0	0	1	1

我们在邮政编码中发现了1个噪声数据。我们删除了相应的样本，因为它只有4位数，而该特征的其他值都有5位数。

# 导入必要的库
import pandas as pd

# 读取数据集
df = pd.read_csv('data.csv')

# 删除'ZIP Code'列中小于20000的行
df.drop(df[df['ZIP Code'] < 20000].index, inplace=True)

# 重置索引
df.reset_index(drop=True, inplace=True)

# 注释：
# 1. 导入pandas库，用于数据处理和分析
# 2. 读取名为'data.csv'的数据集，并将其存储在变量df中
# 3. 使用布尔索引，找到'ZIP Code'列中小于20000的行，并将其索引传递给drop函数
# 4. inplace=True表示在原始数据集上进行修改，即删除满足条件的行
# 5. 使用reset_index函数重置索引，drop=True表示不保留原始索引，inplace=True表示在原始数据集上进行修改

II) 经验噪音处理：

如第三步所示，数据集中包含了Experience的负值。考虑到该特征表示的是工作经验的年数，这些负值被认为是噪声：

# 统计数据框df中Experience列中小于0的值的数量
df[df['Experience'] < 0]['Experience'].count()

52

统计唯一的负值数量：

# 导入必要的库
import pandas as pd

# 读取数据集
df = pd.read_csv('data.csv')

# 选择Experience列中小于0的行，并计算每个值的出现次数
negative_experience_counts = df[df['Experience'] < 0]['Experience'].value_counts()

# 打印结果
print(negative_experience_counts)

# 注释：
# 1. 导入pandas库，用于数据处理和分析
# 2. 读取名为data.csv的数据集，并将其存储在名为df的DataFrame对象中
# 3. 选择Experience列中小于0的行，使用布尔索引进行筛选
# 4. 对筛选后的Experience列进行值计数，统计每个值的出现次数
# 5. 将结果存储在名为negative_experience_counts的Series对象中
# 6. 打印negative_experience_counts，显示每个负值经验的出现次数

-1    33
-2    15
-3     4
Name: Experience, dtype: int64

由于经验特征中这些噪声值的数量很少，我们假设这些值被错误地记录为负值，并将其替换为它们的绝对值：

# 给DataFrame中的'Experience'列的每个元素取绝对值
df['Experience'] = df['Experience'].apply(abs)

步骤 5.2：异常值处理

任务：请翻译以下markdown为中文，请保留markdown的格式，并输出翻译结果。

语料:
异常值 是数据集中明显高于或低于大多数其他值的数据点。

峰度 是分布的“尾部”或形状的度量。如果峰度值大于3，则变量很可能包含异常值。这是因为过度的峰度表明数据点在尾部的集中程度高于正常水平，这可能表明存在异常值。

在第三步中，所有连续特征中，只有 抵押贷款 特征的峰度值超过了3。为了检测该特征中可能存在的异常值，我们使用 Z-score技术。

让我们再次看一下抵押贷款的分布情况：

# 设置图表的字体大小
sns.set(rc={'axes.labelsize': 15})

# 创建一个包含两个子图的图表
fig, ax = plt.subplots(1, 2, figsize=(15, 5), dpi=120)

# 在第一个子图中绘制Mortgage的直方图
sns.histplot(x='Mortgage', data=df, color='royalblue', ax=ax[0])

# 在第二个子图中绘制Mortgage的箱线图
sns.boxplot(x='Mortgage', data=df, color='royalblue', ax=ax[1])

# 设置总标题
plt.suptitle('Mortgage Distribution', fontsize=20)

# 调整子图的布局
plt.tight_layout()

# 显示图表
plt.show()

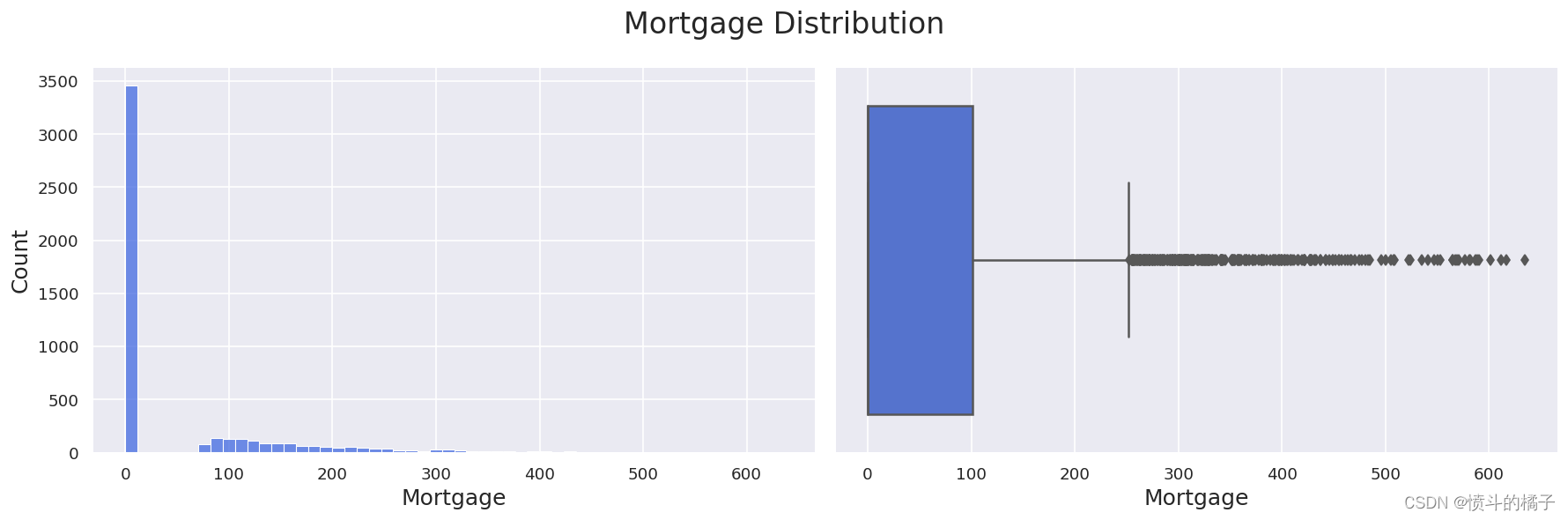
Z-score方法用于异常值检测，是一种统计技术，通过计算每个数据点与均值相差多少个标准差来检测数据集中的异常值。如果一个数据点的Z得分超过了3个标准差，那么它被认为是一个异常值。我们使用scipy.stats模块来执行zscore技术：

# 通过布尔值的Series筛选出'Mortgage'列中标准分数大于3的数据，并计算数量
outlier_count = df[is_outlier]['Mortgage'].count()

105

我们发现了105条Z分数抵押贷款价值大于3的记录。因此，我们将这105条记录视为异常值，并从我们的数据集中过滤掉这些记录。

# 根据'Mortgage'列的z-score值，找出异常值的索引
outlier_indexes = df[stats.zscore(df['Mortgage']) > 3].index

# 删除包含异常值的行
df.drop(outlier_indexes, inplace=True)

# 重置索引
df.reset_index(drop=True, inplace=True)

步骤 5.3: 缺失值处理

在第三步中，我们发现我们的数据集不包含任何__缺失值__。现在让我们再次检查是否有任何缺失值：

# 给定的代码是用来计算DataFrame中缺失值的总数的
# df.isnull()会返回一个与DataFrame df相同大小的布尔型DataFrame，其中缺失值为True，非缺失值为False
# df.isnull().sum()会对每一列进行求和操作，得到一个Series，其中每个元素表示该列中缺失值的数量
# df.isnull().sum().sum()会对Series中的所有元素进行求和操作，得到DataFrame中所有列的缺失值总数
# 最终的结果是一个整数，表示DataFrame中所有列的缺失值总数
df.isnull().sum().sum()

0

数据集中明显没有缺失值。

步骤 5.4：重复值处理

重复值处理 是在将数据集输入机器学习算法之前，从数据集中删除重复记录的过程。这是为了确保只使用唯一的样本来训练和评估机器学习算法：

# 对所有重复行的求和结果再次进行求和操作
df[df.duplicated(keep=False)].sum().sum()

0.0

数据集中明显没有重复项。

步骤 5.5：特征转换

在数据集中，CCAVG代表平均每月信用卡消费，而Income代表年收入金额。
为了使特征的单位相等，我们将平均每月信用卡消费转换为年度消费金额：

# 将df数据框中的'CCAvg'列的值乘以12，得到每年的信用卡平均支出

df['CCAvg'] = df['CCAvg']*12

第六步：双变量分析

在第3步中，我们单独考虑了每个变量的单变量分析，现在我们将再次考虑它们与目标变量的关系。

首先，我们将确定目标变量与分类特征之间的关系。然后，我们将比较数值特征与目标变量。

步骤 6.1：分类特征与目标变量

在这部分中，我们将创建100%堆叠条形图和柱状图，分别显示每个分类特征类别中购买和未购买贷款的比例。

# 定义一个包含数据集中重要分类特征名称的列表
Cat_Features = ['CD Account','Education','Family','Securities Account','Online','Securities Account']

# 为了简化操作，将目标变量的名称定义为一个变量
Target = 'Personal Loan'

# 创建一个2行3列的图表，大小为15x12，分辨率为200
fig, ax = plt.subplots(nrows=2, ncols=3, figsize=(15,12), dpi=200)

# 遍历Cat_Features列表中的每个元素
for i,col in enumerate(Cat_Features):
    
    # 创建一个交叉表，显示每个特征类别中购买和未购买贷款的比例
    cross_tab = pd.crosstab(index=df[col], columns=df[Target])
    
    # 使用normalize=True参数可以得到按索引归一化的数据比例
    cross_tab_prop = pd.crosstab(index=df[col], columns=df[Target], normalize='index')

    # 定义颜色映射
    cmp = ListedColormap(['royalblue', 'darkturquoise'])
    
    # 绘制堆叠条形图
    x, y = i//3, i%3
    cross_tab_prop.plot(kind='bar', ax=ax[x,y], stacked=True, width=0.8, colormap=cmp,
                        legend=False, ylabel='Proportion', sharey=True)
    
    # 在图表中添加每个条形的比例和计数
    for idx, val in enumerate([*cross_tab.index.values]):
        for (proportion, count, y_location) in zip(cross_tab_prop.loc[val],cross_tab.loc[val],cross_tab_prop.loc[val].cumsum()):
            ax[x,y].text(x=idx-0.22, y=(y_location-proportion)+(proportion/2)-0.03,
                         s = f'  {count}\n({np.round(proportion * 100, 1)}%)', 
                         color = "black", fontsize=9, fontweight="bold")
    
    # 添加图例
    ax[x,y].legend(title='Personal Loan', loc=(0.7,0.9), fontsize=8, ncol=2)
    # 设置y轴范围
    ax[x,y].set_ylim([0,1.12])
    # 旋转x轴刻度标签
    ax[x,y].set_xticklabels(ax[x,y].get_xticklabels(), rotation=0)
            

# 设置总标题
plt.suptitle('Categorical Features vs Target Stacked Barplots', fontsize=22)
plt.tight_layout()                     
plt.show()

结论:

• 拥有银行存款证书（CD）的客户似乎会从银行购买个人贷款。

• 受教育程度较高的客户更有可能购买个人贷款。

• 家庭成员数量对购买个人贷款的概率没有显著影响。

• 在银行拥有或不拥有证券账户的客户对购买个人贷款的概率没有影响。

• 使用或不使用网上银行的客户似乎对购买个人贷款的概率没有任何影响。

• 使用或不使用信用卡的客户似乎对购买个人贷款的可能性没有影响。

步骤 6.2：数值特征 vs 目标变量

在这部分中，我们将尝试找出购买个人贷款的客户与不购买个人贷款的客户之间数值特征的 平均值 和 分布情况。

# 定义一个包含数据集中重要数值特征名称的列表
Num_Features = ['CCAvg','Income','Mortgage','Age','Experience']

# 设置颜色主题
sns.set_palette(['royalblue', 'darkturquoise'])

# 创建一个包含5行2列的图表，设置图表大小为15x15，分辨率为200dpi，设置宽度比例为1:2
fig, ax = plt.subplots(5, 2, figsize=(15,15), dpi=200, gridspec_kw={'width_ratios': [1, 2]})

# 遍历Num_Features列表中的每个特征
for i, col in enumerate(Num_Features):
    # 创建柱状图
    graph = sns.barplot(data=df, x=Target, y=col, ax=ax[i,0])
    
    # 创建核密度估计图
    # 绘制Target为0的数据的核密度曲线，设置填充，线宽为2，图表为ax[i,1]，标签为'0'
    sns.kdeplot(data=df[df[Target]==0], x=col, fill=True, linewidth=2, ax=ax[i,1], label='0')
    # 绘制Target为1的数据的核密度曲线，设置填充，线宽为2，图表为ax[i,1]，标签为'1'
    sns.kdeplot(data=df[df[Target]==1], x=col, fill=True, linewidth=2, ax=ax[i,1], label='1')
    
    # 设置y轴刻度为空
    ax[i,1].set_yticks([])
    # 设置图例标题为'Personal Loan'，位置为右上角
    ax[i,1].legend(title='Personal Loan', loc='upper right')
    
    # 为柱状图添加标签
    for cont in graph.containers:
        graph.bar_label(cont, fmt='         %.3g')

# 设置总标题为'Numerical Features vs Target Distribution'，字体大小为22
plt.suptitle('Numerical Features vs Target Distribution', fontsize=22)
# 调整子图布局
plt.tight_layout()
# 显示图表
plt.show()

结论:

• 在信用卡上花费更多的客户更有可能申请个人贷款。

• 收入较高的客户更有可能购买个人贷款。

• 抵押贷款价值较高的客户更有可能购买个人贷款。

• 可以推断出客户的年龄对购买个人贷款的概率没有影响。

• 工作经验对贷款购买的影响与客户年龄类似。经验的分布与年龄的分布非常相似，因为经验与年龄强相关。

因此，我们移除经验，因为它提供的信息与年龄相比没有更多的价值。

# 删除数据框df中的'Experience'列
# 参数axis=1表示按列删除，inplace=True表示在原数据框上进行修改
df.drop('Experience', axis=1, inplace=True)

第七步：训练测试分割

首先，需要定义给定数据集的特征（X）和输出标签（y）。X是一个包含所有给定观测的不同特征值的数据框，而y是一个包含每个观测所属的分类标签的系列。

# 从DataFrame中删除'Personal Loan'列，并将结果赋值给X
X = df.drop('Personal Loan', axis=1)

# 从DataFrame中提取'Personal Loan'列，并将结果赋值给y
y = df['Personal Loan']

我们需要在监督式机器学习中执行 训练测试拆分 ，以在模型训练后评估其性能。数据集通常被分为两部分：训练集用于训练模型，测试集用于衡量模型在新数据上的表现。训练测试拆分允许我们通过检查模型在未见数据上的性能来评估其泛化能力。这种技术可以用于识别模型中的任何偏差和方差，并确保它在未见示例上具有良好的泛化能力。

不平衡数据集：

不平衡数据集是指类别不平衡或不相等的数据集。这意味着每个目标类别的样本数量不平等，某些类别可能比其他类别有更多的样本。

正如我们在第3步中所看到的，我们正在处理的数据集是一个不平衡的数据集。让我们再次检查一下：

import matplotlib.pyplot as plt

# 创建一个图形对象，设置dpi为80
plt.figure(dpi=80)

# 绘制频率百分比的条形图
df['Personal Loan'].value_counts(normalize=True).mul(100).plot(kind='barh', width=0.8, figsize=(8,5))

# 将频率百分比添加到图中
labels = df['Personal Loan'].value_counts(normalize=True).mul(100).round(1)
for i in labels.index:
    # 在图中的每个条形上添加文本，显示百分比
    plt.text(labels[i], i, str(labels[i])+ '%', fontsize=15, weight='bold')

# 设置x轴的范围为0到110
plt.xlim([0, 110])
# 设置x轴标签为"Frequency Percentage"，字体大小为15
plt.xlabel('Frequency Percentage', fontsize=15)
# 设置y轴标签为"Personal Loan"，字体大小为15
plt.ylabel('Personal Loan', fontsize=15)
# 设置图的标题为"Frequency Percentage of Target Classes"，字体大小为15
plt.title('Frequency Percentage of Target Classes', fontsize=15)
# 显示图形
plt.show()

如您所见，我们正在处理的数据集是不平衡的。

不平衡数据集的问题：

1. 不平衡的数据集可能导致算法对多数类别有偏见。这意味着在不平衡的数据集上训练的任何分类算法通常会将少数类别错误地分类为多数类别。

2. 当机器学习模型使用不平衡数据进行训练时，其性能可能会严重偏向某一类别。例如，我们的数据集中有91.2%的0类和8.8%的1类，那么学习模型可能很容易优化为将所有测试输入预测为属于0类，并且仍然能够获得91.2%的准确率！

3. 如果模型在严重不平衡的数据上进行训练，它可能会对数据中的潜在趋势产生错误的理解。模型可能无法识别某些值在不同类别之间的分布方式，甚至无法识别某些类别之间的重叠情况。

处理不平衡数据集的技术：

1. 训练测试分割的方法：

处理不平衡数据集时，训练测试分割的方法是使用分层抽样（stratification）。分层抽样是将不平衡数据集分割成训练集和测试集的重要步骤。分层抽样确保每个类别在训练集和测试集中的比例保持一致。这一点很重要，因为它可以更准确地评估模型，避免由于某个类别在任一数据集中过度表示而导致的偏差。分层抽样还确保在将数据集分割成训练集和测试集后，保留了整个数据集中不同类别之间存在的任何趋势或相关性。

# 导入train_test_split函数用于划分训练集和测试集
from sklearn.model_selection import train_test_split

# 使用train_test_split函数划分数据集
# X为特征数据，y为目标数据
# test_size=0.2表示将数据集划分为80%的训练集和20%的测试集
# random_state=0表示随机种子，保证每次划分的结果相同
# stratify=y表示按照y的类别比例划分数据集，保证训练集和测试集中各类别的比例相同
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)

让我们来看看训练集和测试集中每个类别的比例：

# 定义一个包含频率百分比的数据框
df_perc = pd.concat([y.value_counts(normalize=True).mul(100).round(1),
                     y_train.value_counts(normalize=True).mul(100).round(1),
                     y_test.value_counts(normalize=True).mul(100).round(1)], axis=1)
df_perc.columns=['Dataset','Training','Test']
df_perc = df_perc.T

# 绘制频率百分比的条形图
df_perc.plot(kind='barh', stacked=True, figsize=(10,5), width=0.6)

# 在图上添加百分比
for idx, val in enumerate([*df_perc.index.values]):
    for (percentage, y_location) in zip(df_perc.loc[val], df_perc.loc[val].cumsum()):
        plt.text(x=(y_location - percentage) + (percentage / 2)-3,
                 y=idx - 0.05,
                 s=f'{percentage}%', 
                 color="black",
                 fontsize=12,
                 fontweight="bold")

# 添加图例
plt.legend(title='Personal Loan', loc=(1.01,0.8))
plt.xlabel('Frequency Percentage', fontsize=15)
plt.title('Frequency Percentage of Target Classes among Training and Test Sets', fontsize=15)
plt.show()

如上所示，样本被随机分割，以保证每个类别在训练集和测试集中的比例保持一致。

2. 模型评估的方法：

处理不平衡数据集时，模型评估的方法是使用适当的指标，包括召回率（recall）、精确率（precision）、F1分数和AUC（曲线下面积），这些指标在处理不平衡数据集时比传统的准确率指标更合适，因为传统准确率指标默认不考虑类别不平衡的情况。

在这个项目中，主要目标是对可能购买贷款的潜在客户进行分类。用于评估模型性能的指标将对确定模型能够多好地识别这些潜在客户起重要作用。

• 召回率是模型正确识别的实际正例比例的度量。高召回率意味着模型的假阴性数量较低，在这个项目中是可取的，因为这意味着模型没有错过太多潜在的贷款客户。

• 精确率是模型识别的正例中实际为正例的比例的度量。高精确率意味着模型的假阳性数量较低，在这个项目中是可取的，因为这意味着模型没有将太多的非贷款客户识别为潜在贷款客户。

• F1分数是召回率和精确率之间的权衡的度量。它被计算为召回率和精确率的调和平均值。高F1分数表示召回率和精确率之间的平衡。

对于这个项目，类别 ‘1’ 的召回率和精确率都是重要的指标，所以类别 ‘1’ 的F1分数应被视为最重要的指标。高F1分数表示在尽可能识别出多个潜在贷款客户（高召回率）的同时，最小化误识别的非贷款客户（高精确率）之间的平衡。这对于银行来说很重要，因为它希望提高存款人转为借款人的转化率，同时降低营销活动的成本。

3. 模型构建的方法：

I) 基于数据的方法：

• 随机欠采样：欠采样是指随机从多数类中删除实例，以减小其大小。

  • 缺点：丢弃大部分训练集导致信息丢失。

• 随机过采样：它涉及向少数类中添加额外的实例副本，使其大小更加平衡。

  • 缺点：过拟合，由于复制少数类的观察而引起。

• SMOTE：SMOTE（合成少数类过采样技术）是一种过采样技术，它从少数类中创建新的合成观察结果。通过这种方式，算法避免了随机过采样导致的过拟合问题。

  • 缺点：由于SMOTE随机创建新数据行，新创建的合成样本缺乏真实的价值信息，从而可能导致整体准确性降低。此外，如果存在类之间的自然边界，例如重叠的类，由于通过SMOTE人工创建数据点，可能会产生额外的异常值。

II) 基于模型的方法：

• 惩罚算法：通过给定更多权重给特定的分类标签，使得对少数类的正确分类比对多数类的正确分类在优化过程中更加重要。

• 使用基于树的算法：基于树的算法如随机森林、极端随机树和XGBoost可以自然地处理不平衡数据，因为它们根据随机决策树的多数投票来做出决策，并且在训练之前不需要平衡类别。

考虑到基于数据的方法的缺点，我们将只实施基于模型的方法。

第八步：特征选择

特征选择 是选择用于模型构建的相关特征子集的过程。

特征选择的优势：

1. 提高准确性：当特征较少时，模型需要学习的方面较少，这可能导致在预测新数据时产生较少的错误。

2. 提高解释性：特征选择有助于识别重要特征，并通过从数据集中删除冗余或不相关的特征使模型更具解释性。

3. 更快的训练时间：特征选择通过减少需要进行的计算数量来降低计算成本，以便训练和测试模型。这反过来减少了训练时间，使模型更高效。

4. 减少过拟合：通过从数据中删除不相关和冗余的特征，特征选择还可以帮助减少过拟合。过拟合可能发生在模型中包含过多变量而没有足够的观测或应用正则化技术的情况下。

特征选择方法：

I) 包装方法：

这些方法使用预测模型对每个特征子集进行评分，并确定每个特征的重要性。最重要的包装方法有：

• 前向选择： 前向选择是一种迭代的特征选择方法，它从模型中没有特征开始，逐个将最具预测性的特征添加到模型中，当验证分数没有改善时停止。这个过程重复进行，直到满足某些条件或考虑了所有可能的特征集合。通过使用度量标准，算法可以确定哪些特征组合最能改善模型性能。前向选择的结果是一个有序列表，根据其对提高模型准确性的贡献对特征的重要性进行排名。

• 置换： 置换通过对特征的值进行洗牌，从而创建一个随机排列，测量模型准确性下降的程度来评估给定特征的影响。准确性下降越大，该特征对解决手头任务的重要性就越大。

• 删除列： 这个方法的思想是计算所有预测变量的模型性能，并删除一个单独的预测变量，观察性能的降低程度。特征越重要，模型性能下降越大。

II) 过滤方法：

这些方法使用统计量度量，例如：

• 相关系数
• 信息增益
• 卡方检验

III) 嵌入方法：

嵌入方法结合了过滤方法和包装方法的元素，通过在特征选择过程中构建预测模型来更好地评估潜在特征。嵌入方法的示例包括：

• LASSO回归
• 决策树
• 随机森林
• 梯度提升机（GBM）

我们将继续使用删除列特征重要性方法，因为它实际上是计算特征重要性的最准确的方式。

注意：删除列方法不能反映出特征本身的内在预测价值，而是反映了该特征对特定模型的重要性。

步骤 8.1：删除列特征重要性实现

正如我们之前讨论的那样，对于这个项目来说，类别’1’的f1-score应被视为最重要的指标。

# 定义一个评分函数
def f1_metric(model, X_train, y_train):
    '''
    这个函数用于报告指定类别（正类别或者1）的f1-score指标
    '''
    return f1_score(y_train, model.predict(X_train), average='binary')

克隆模型 可以用于创建同一模型的多个版本。这样，可以使用不同的参数或数据集测试模型的不同版本。这可以更全面和准确地评估模型，以避免一个版本过度偏向于先前的版本。此外，了解稍微不同的参数如何影响模型的性能可能是有益的。通过克隆模型，我们可以快速轻松地生成多个模型并进行并行测试。

接下来，我们将通过一个使用克隆的函数来实现删除列特征重要性技术：

def drop_column_importance(model, X_train, y_train, random_state=0):
    # 创建一个空列表来存储特征重要性
    importances = []
    
    # 克隆模型
    model_clone = clone(model)
    
    # 设置随机种子以确保可比性
    model_clone.random_state = random_state
    
    # 训练模型
    model_clone.fit(X_train, y_train)
    
    # 使用StratifiedKFold创建交叉验证对象
    cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=0)
    
    # 使用交叉验证评估基准模型的得分
    benchmark_score = cross_val_score(model_clone, X_train, y_train, cv=cv, scoring=f1_metric).mean()

    # 遍历所有特征并存储特征重要性
    for col in X_train.columns:
        # 克隆模型
        model_clone = clone(model)
        
        # 设置随机种子以确保可比性
        model_clone.random_state = random_state
        
        # 在删除一个特征的数据集上训练模型
        model_clone.fit(X_train.drop(col, axis=1), y_train)
        
        # 评估删除特征后的模型得分
        drop_column_score = cross_val_score(model_clone, X_train.drop(col, axis=1), y_train, cv=cv, scoring=f1_metric).mean()
        
        # 存储特征重要性，定义为基准模型得分与删除特征后模型得分之差
        importances.append(benchmark_score - drop_column_score)
        
    # 将特征及其重要性以DataFrame的形式返回
    importances_df = pd.DataFrame({'feature': X_train.columns, 'feature importance': importances}) \
                     .sort_values('feature importance', ascending=False).reset_index(drop=True)
           
    return importances_df

任务：请翻译以下markdown为中文，请保留markdown的格式，并输出翻译结果。

语料:
定义一个函数来使用条形图来可视化删除列特征重要性技术的结果：

def drop_column_importance_plot(model, X_train, y_train):
    # 调用drop-column特征重要性函数
    df_drop_column = drop_column_importance(model, X_train, y_train, random_state=0)
    # 重命名列名
    df_drop_column.columns = ['Feature', 'Feature Importance']
    
    # 绘制条形图
    plt.figure(figsize=(12,10))
    sns.barplot(data=df_drop_column, x='Feature Importance', y='Feature', orient='h', color='royalblue')
    plt.title('Drop Column Feature Importance', fontsize=20)
    plt.show()

在接下来的步骤中，我们将在构建最终模型之前使用这些函数来检测冗余特征，针对每个分类算法。

第九步：朴素贝叶斯模型构建

朴素贝叶斯

朴素贝叶斯 是一种机器学习中的 分类 算法。它用于预测给定输入属于不同类别的概率。它基于贝叶斯定理，利用类别的先验概率和给定类别的特征的似然概率来计算类别的后验概率。然后选择具有最高后验概率的类别作为输入的预测类别。朴素贝叶斯分类器算法对数据和问题做出了几个假设。

朴素贝叶斯的主要假设：

1. 独立性： 该算法假设数据中的所有特征在给定类别的情况下相互独立。这是算法中的“朴素”部分，在现实世界的问题中通常是不现实的，但它可以提供计算效率高的解决方案。

2. 条件独立性： 该算法还假设特征在给定类别的情况下是条件独立的，这意味着给定其他特征的情况下，一个特征的概率与其他特征无关。

3. 常数类别先验概率： 该算法假设类别的先验概率是常数，并且不随数据而变化。

注意： 朴素贝叶斯的基本假设已经满足，因为只有两个特征高度相关，即经验和年龄，而经验特征已经在之前被移除。

sklearn中可用的不同类型的朴素贝叶斯算法：

• 高斯朴素贝叶斯： 当数据是连续的且符合__正态__分布时使用该算法。

• 多项式朴素贝叶斯： 当数据是离散的且表示每个类别的__出现次数__时使用该算法。

• 伯努利朴素贝叶斯： 该算法类似于多项式朴素贝叶斯，但当数据是__二进制__时使用。

• 补充朴素贝叶斯： 该算法类似于多项式朴素贝叶斯，但专为__不平衡数据集__设计。

• 分类朴素贝叶斯： 该算法类似于多项式朴素贝叶斯，但专为__分类数据而不是计数数据__设计。

在这个项目中，我们的数据集包含了具有不同分布的特征：

• 连续特征 - 年龄，收入，CCAvg，抵押贷款
• 二进制特征 - 证券账户，CD账户，在线，信用卡
• 多项式特征 - 家庭
• 分类特征 - 教育，邮政编码

策略：

• 第一策略 是在数据的连续部分上独立拟合高斯NB模型，在多项式部分上拟合补充NB模型（不平衡数据集），在伯努利部分上拟合伯努利模型，并在分类部分上拟合分类NB模型。在将每个模型拟合到相应的数据部分之后，我们通过使用预测概率（使用predict_proba方法）作为新特征来转换数据集，然后在新特征上重新拟合一个新的高斯NB模型。

• 第二策略 是将连续特征离散化，并应用不同的基于离散数据的朴素贝叶斯模型，包括补充NB和伯努利NB，以找到性能最佳的模型。

我们将实施__第二个策略__，因为根据步骤6.2，收入，CCAvg和抵押贷款是重要特征，但它们的分布不是正态分布，且具有较高的偏度和峰度，这在执行高斯NB时会导致较大的误差。

步骤 9.1：补充朴素贝叶斯模型构建

多项式朴素贝叶斯（Multinomial NB） 是一种常用于文本分类任务的概率分类器。它基于这样的假设：给定类别标签，文本中的特征（例如单词）在条件独立性下成立。多项式朴素贝叶斯使用多项式分布来建模给定类别标签时每个特征的概率。

补充朴素贝叶斯（Complement NB） 是多项式朴素贝叶斯算法的一种变体，旨在纠正多项式朴素贝叶斯算法中固有的偏差。多项式朴素贝叶斯算法倾向于为具有更多训练样本的类别分配更高的概率。补充朴素贝叶斯通过计算标准朴素贝叶斯概率估计的补集，并使用这些补集概率进行预测，以纠正这种偏差。

由于我们的数据集不平衡，我们将使用补充朴素贝叶斯（CNB）而不是多项式朴素贝叶斯（MNB）。

步骤 9.1.1：补充朴素贝叶斯特征离散化

KBinsDiscretizer类来自scikit-learn，提供了使用分箱方法进行离散化的实现。它允许我们在不同的箱数（n_bins）和分箱策略之间进行选择。

我们将定义一个包含GridSearchCV类的函数，以找到最佳的n_bins和strategy组合。换句话说，我们尝试在定义的范围内尝试所有的n_bins和strategy组合，并使用考虑的NB模型来评估离散化器在验证集上的性能，以找到最佳的组合。

def discretization_report(df, clf):
    '''
    这个函数找到连续特征离散化的最佳组合n_bins和strategy
    '''
    # 定义要进行离散化的连续特征
    cols_to_discretize = ['Age', 'Income', 'CCAvg', 'Mortgage']

    # 定义特征（X）和输出标签（y）
    X = df[cols_to_discretize]
    y = df['Personal Loan']

    # 将数据集拆分为训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)

    # 定义网格搜索参数
    param_grid = {'discretizer__strategy': ['uniform', 'quantile', 'kmeans'],
                  'discretizer__n_bins': np.arange(2,11)}

    # 定义KBinsDiscretizer、OneHotEncoder和ComplementNB对象
    discretizer = KBinsDiscretizer(encode='ordinal')
    onehot = OneHotEncoder(handle_unknown='ignore', drop='first')

    # 创建流水线
    pipeline = Pipeline([('discretizer', discretizer), ('onehot', onehot), ('clf', clf)])

    # 使用StratifiedKFold创建交叉验证对象，以确保所有折叠中的类分布相同
    cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=0)

    # 创建GridSearchCV对象
    grid_search = GridSearchCV(pipeline, param_grid, cv=cv, scoring='f1')
    
    # 将GridSearchCV对象拟合到训练数据上
    grid_search.fit(X_train, y_train)

    # 打印最佳参数和最佳得分
    print("最佳离散化参数:", grid_search.best_params_)
    print("最佳得分:", grid_search.best_score_)
    
    # 返回n_bins和strategy的最佳值
    return grid_search.best_params_['discretizer__n_bins'], grid_search.best_params_['discretizer__strategy']

任务：请使用discretization_report函数找到KBinsDiscretizer参数的最佳值。

# 忽略一个警告，警告可能在某些情况下，箱子的宽度太小
warnings.simplefilter(action='ignore')

# 初始化CNB分类器
cnb = ComplementNB()

# 调用discretization_report函数
n_bins, strategy = discretization_report(df, cnb)

Best discretization parameters: {'discretizer__n_bins': 6, 'discretizer__strategy': 'quantile'}
Best score: 0.5354708442834474

最佳的n_bins和strategy值在考虑CNB模型时得到：

• n_bins : 6
• strategy : quantile（每个特征中的所有bin具有相同数量的数据点）

步骤 9.1.2：补充 NB 特征编码

在获得了KBinsDiscretizer参数的最优值（包括n_bins和strategy）之后，我们使用这些最优参数对连续特征进行离散化处理。然后，我们对非二进制分类特征进行虚拟编码。我们定义了一个用于特征编码的函数：

def nb_feature_encoding(df, n_bins, strategy, cols_to_encode):
    '''
    这个函数在考虑到最佳的n_bins和strategy值之后，对所需的分类特征进行特征离散化后执行虚拟编码。
    '''
    # 定义要进行离散化的连续特征
    cols_to_discretize = ['Age', 'Income', 'CCAvg', 'Mortgage']

    # 定义特征（X）和输出标签（y）
    X = df.drop('Personal Loan', axis=1)
    y = df['Personal Loan'] 

    # 将数据集拆分为训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)

    # 对连续特征进行离散化
    discretizer = KBinsDiscretizer(n_bins=n_bins, strategy=strategy, encode='ordinal')
    X_train[cols_to_discretize] = discretizer.fit_transform(X_train[cols_to_discretize])
    X_test[cols_to_discretize] = discretizer.transform(X_test[cols_to_discretize])

    # 对离散化后的特征进行独热编码
    X_train = pd.get_dummies(X_train, columns=cols_to_encode, drop_first=True)
    X_test = pd.get_dummies(X_test, columns=cols_to_encode, drop_first=True)
    
    # 将测试集的列与训练集对齐
    X_test = X_test.reindex(columns=X_train.columns, fill_value=0)
    
    # 返回转换后的特征
    return X_train, X_test

应用nb_feature_encoding函数对所需特征进行onehot编码：

# 定义函数 nb_feature_encoding，用于对非二进制特征进行独热编码
def nb_feature_encoding(df, n_bins, strategy, cols_to_encode):
    # 创建一个新的 DataFrame，用于存储编码后的特征
    encoded_df = pd.DataFrame()
    
    # 遍历需要编码的特征
    for col in cols_to_encode:
        # 将特征的值转换为二维数组形式
        feature_values = df[col].values.reshape(-1, 1)
        
        # 使用 KBinsDiscretizer 对特征进行分箱处理
        enc = KBinsDiscretizer(n_bins=n_bins, encode='onehot', strategy=strategy)
        encoded_feature = enc.fit_transform(feature_values)
        
        # 将编码后的特征转换为 DataFrame，并添加到 encoded_df 中
        encoded_feature_df = pd.DataFrame(encoded_feature.toarray(), columns=enc.get_feature_names_out([col]))
        encoded_df = pd.concat([encoded_df, encoded_feature_df], axis=1)
    
    # 将编码后的特征与原始数据集的其他特征进行合并
    encoded_df = pd.concat([encoded_df, df.drop(cols_to_encode, axis=1)], axis=1)
    
    # 将数据集划分为训练集和测试集
    X_train = encoded_df[:len(df_train)]
    X_test = encoded_df[len(df_train):]
    
    return X_train, X_test

# 定义需要进行独热编码的非二进制特征列表
cols_to_encode = ['Age', 'Income', 'CCAvg', 'Mortgage', 'Family', 'Education']

# 调用 nb_feature_encoding 函数对数据集进行特征编码
X_train, X_test = nb_feature_encoding(df, n_bins, strategy, cols_to_encode)

步骤 9.1.3：补充朴素贝叶斯特征子集选择

为了找到考虑CNB模型的最重要特征，我们使用之前定义的drop_column_importance_plot函数。

# 初始化CNB分类器
cnb = ComplementNB()

# 调用drop_column_importance_plot函数，绘制特征重要性图
drop_column_importance_plot(cnb, X_train, y_train)

负重要性在删除列特征重要性中意味着从模型中删除相应的特征实际上会改善模型性能。因此，我们对数据集进行筛选：

# 调用函数计算特征重要性并删除重要性为0的特征
feature_importances = drop_column_importance(cnb, X_train, y_train, 0)

# 选择重要性大于0的特征
selected_features = feature_importances[feature_importances['feature importance'] > 0]['feature']

# 根据选择的特征过滤训练集和测试集
X_train = X_train[selected_features]
X_test = X_test[selected_features]

步骤 9.1.4：补充朴素贝叶斯模型构建

在删除不相关的特征后，我们训练最终的CNB模型：

# 导入ComplementNB模型
from sklearn.naive_bayes import ComplementNB

# 创建ComplementNB模型的实例
cnb = ComplementNB()

# 使用训练数据X_train和对应的标签y_train来训练ComplementNB模型
cnb.fit(X_train, y_train)

ComplementNB()

步骤 9.1.5：补充朴素贝叶斯模型评估

为了评估模型的性能，我们定义了一个函数，这样它就可以用来评估后续的模型。

# 定义一个函数metrics_calculator用于计算给定模型在测试数据上的所有性能指标
def metrics_calculator(clf, X_test, y_test, model_name):
    '''
    This function calculates all desired performance metrics for a given model on test data.
    '''
    # 使用给定的模型对测试数据进行预测
    y_pred = clf.predict(X_test)
    
    # 创建一个包含所有性能指标的数据框result
    result = pd.DataFrame(data=[accuracy_score(y_test, y_pred),  # 准确率
                                precision_score(y_test, y_pred, average='binary'),  # 精确率
                                recall_score(y_test, y_pred, average='binary'),  # 召回率
                                f1_score(y_test, y_pred, average='binary'),  # F1分数
                                roc_auc_score(y_test, clf.predict_proba(X_test)[::,1])],  # AUC值
                          index=['Accuracy','Precision','Recall','F1-score','AUC'],  # 指标名称
                          columns = [model_name])  # 模型名称
    
    # 将结果转换为百分比形式，并保留两位小数
    result = (result * 100).round(2).astype(str) + '%'                            
    
    # 返回结果
    return result

# 模型评估函数

def model_evaluation(clf, X_train, X_test, y_train, y_test, model_name):
    '''
    该函数提供了模型性能的完整报告，包括分类报告、混淆矩阵和ROC曲线。
    '''

    # 设置字体大小
    sns.set(font_scale=1.2)
    
    # 生成训练集的分类报告
    y_pred_train = clf.predict(X_train)
    print("\n\t  训练集的分类报告")
    print("-"*55)
    print(classification_report(y_train, y_pred_train))

    # 生成测试集的分类报告
    y_pred_test = clf.predict(X_test)
    print("\n\t   测试集的分类报告")
    print("-"*55)
    print(classification_report(y_test, y_pred_test))
    
    # 创建图形和子图
    fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5), dpi=100, gridspec_kw={'width_ratios': [2, 2, 1]})
    
    # 绘制测试集的混淆矩阵
    ConfusionMatrixDisplay.from_estimator(clf, X_test, y_test, colorbar=False, cmap=royalblue_r, ax=ax1)
    ax1.set_title('测试数据的混淆矩阵')                                     
    ax1.grid(False)
    
    # 绘制测试数据的ROC曲线并显示AUC分数
    RocCurveDisplay.from_estimator(clf, X_test, y_test, ax=ax2)
    ax2.set_xlabel('假阳性率')
    ax2.set_ylabel('真阳性率')
    ax2.set_title('测试数据的ROC曲线（正类别: 1）')
    
    # 报告指定正类别的结果
    result = metrics_calculator(clf, X_test, y_test, model_name)
    table = ax3.table(cellText=result.values, colLabels=result.columns, rowLabels=result.index, loc='center')
    table.scale(0.6, 2)
    table.set_fontsize(12)
    ax3.axis('tight')
    ax3.axis('off')
    # 修改颜色
    for key, cell in table.get_celld().items():
        if key[0] == 0:
            cell.set_color('royalblue')
    plt.tight_layout()
    plt.show()

让我们调用上述函数来评估我们的CNB模型：

# 导入所需的库
from sklearn.naive_bayes import ComplementNB
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score

def model_evaluation(model, X_train, X_test, y_train, y_test, model_name):
    """
    模型评估函数，用于评估分类模型的性能指标

    参数：
    model: 分类模型对象
    X_train: 训练集特征数据
    X_test: 测试集特征数据
    y_train: 训练集标签数据
    y_test: 测试集标签数据
    model_name: 模型名称

    返回：
    无返回值，打印模型的性能指标

    """

    # 使用训练集数据拟合模型
    model.fit(X_train, y_train)

    # 使用训练好的模型对测试集数据进行预测
    y_pred = model.predict(X_test)

    # 计算模型的准确率
    accuracy = accuracy_score(y_test, y_pred)

    # 计算模型的精确率
    precision = precision_score(y_test, y_pred, average='weighted')

    # 计算模型的召回率
    recall = recall_score(y_test, y_pred, average='weighted')

    # 计算模型的F1-score
    f1 = f1_score(y_test, y_pred, average='weighted')

    # 打印模型的性能指标
    print(f"模型名称: {model_name}")
    print(f"准确率: {accuracy}")
    print(f"精确率: {precision}")
    print(f"召回率: {recall}")
    print(f"F1-score: {f1}")

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      0.87      0.93      3569
           1       0.41      0.95      0.57       346

    accuracy                           0.88      3915
   macro avg       0.70      0.91      0.75      3915
weighted avg       0.94      0.88      0.90      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      0.85      0.92       892
           1       0.38      0.94      0.54        87

    accuracy                           0.86       979
   macro avg       0.69      0.90      0.73       979
weighted avg       0.94      0.86      0.88       979

我们从Complement NB得到了约94%的召回率，这是不错的，但由于低精确度值为38%，f1-score约为54%。

# 导入metrics_calculator函数，用于计算分类器的性能指标
from 某个模块 import metrics_calculator

# 使用Complement Naive Bayes分类器对测试集进行预测，并计算性能指标
# 将分类器、测试集特征数据X_test、测试集标签数据y_test以及分类器名称'Complement Naive Bayes'作为参数传入metrics_calculator函数
# 将计算得到的性能指标保存在cnb_result变量中
cnb_result = metrics_calculator(cnb, X_test, y_test, 'Complement Naive Bayes')

第9.2步：伯努利朴素贝叶斯模型构建

伯努利朴素贝叶斯（Bernoulli NB）与多项式朴素贝叶斯（MultinomialNB）一样，适用于离散数据。不同之处在于，多项式朴素贝叶斯使用出现次数，而伯努利朴素贝叶斯设计用于处理二进制数据，其中特征要么为真要么为假（1或0）。

步骤 9.2.1：伯努利朴素贝叶斯特征离散化

为了找到考虑伯努利NB的KBinsDiscretizer的最佳值，我们调用discretization_report函数：

# 导入所需的库
from sklearn.naive_bayes import BernoulliNB

# 初始化一个伯努利朴素贝叶斯分类器
bnb = BernoulliNB()

# 调用discretization_report函数，并传入数据集df和分类器bnb作为参数
n_bins, strategy = discretization_report(df, bnb)

Best discretization parameters: {'discretizer__n_bins': 9, 'discretizer__strategy': 'uniform'}
Best score: 0.5184448691429347

最佳的n_bins和strategy值，考虑到BNB模型，如下所示：

• n_bins : 9
• strategy : uniform（每个特征中的所有箱子具有相同的宽度）

步骤 9.2.2：伯努利朴素贝叶斯特征编码

现在，我们使用获得的最佳n_bins和策略对连续特征进行离散化处理。然后，我们需要对所有非二进制特征进行虚拟编码。

由于ZIP Code特征包含大量的类别并且不是一个重要的特征，我们将在伯努利NB建模中将其移除：

# 复制数据框df并命名为df_bnb
df_bnb = df.copy()

# 在df_bnb中删除'ZIP Code'列，axis=1表示按列删除
df_bnb.drop('ZIP Code', axis=1, inplace=True)

应用nb_feature_encoding函数对所有非二进制特征进行onehot编码：

# 定义需要进行独热编码的非二进制特征列表
cols_to_encode = ['Age', 'Income', 'CCAvg', 'Mortgage', 'Family', 'Education']

# 调用 nb_feature_encoding 函数对数据集 df_bnb 进行特征编码
X_train, X_test = nb_feature_encoding(df_bnb, n_bins, strategy, cols_to_encode)

步骤 9.2.3: 伯努利朴素贝叶斯特征子集选择

为了找到考虑BNB模型的最重要特征，我们再次使用之前定义的drop_column_importance_plot函数：

# 初始化BernoulliNB分类器
bnb = BernoulliNB()

# 调用drop_column_importance_plot函数，用于绘制特征重要性图
drop_column_importance_plot(bnb, X_train, y_train)

再次在“删除列特征重要性”中，负重要性意味着从模型中删除相应的特征实际上会改善模型性能。因此，我们对数据集进行筛选：

# 调用函数：计算特征重要性
feature_importances = drop_column_importance(bnb, X_train, y_train, 0)

# 获取重要特征
selected_features = feature_importances[feature_importances['feature importance'] > 0]['feature']

# 筛选训练集和测试集的重要特征
X_train = X_train[selected_features]
X_test = X_test[selected_features]

步骤 9.2.4：伯努利朴素贝叶斯模型构建

在去除不相关的特征后，我们训练最终的BNB模型：

# 创建一个BernoulliNB对象
bnb = BernoulliNB()

# 使用训练数据X_train和标签数据y_train来训练模型
bnb.fit(X_train, y_train)

BernoulliNB()

步骤 9.2.5：伯努利朴素贝叶斯模型评估

评估我们训练的伯努利NB模型的性能，使用model_evaluation函数：

model_evaluation(bnb, X_train, X_test, y_train, y_test, 'Bernoulli NB')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.96      0.98      0.97      3569
           1       0.73      0.55      0.63       346

    accuracy                           0.94      3915
   macro avg       0.85      0.77      0.80      3915
weighted avg       0.94      0.94      0.94      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.95      0.98      0.97       892
           1       0.72      0.51      0.59        87

    accuracy                           0.94       979
   macro avg       0.84      0.74      0.78       979
weighted avg       0.93      0.94      0.93       979

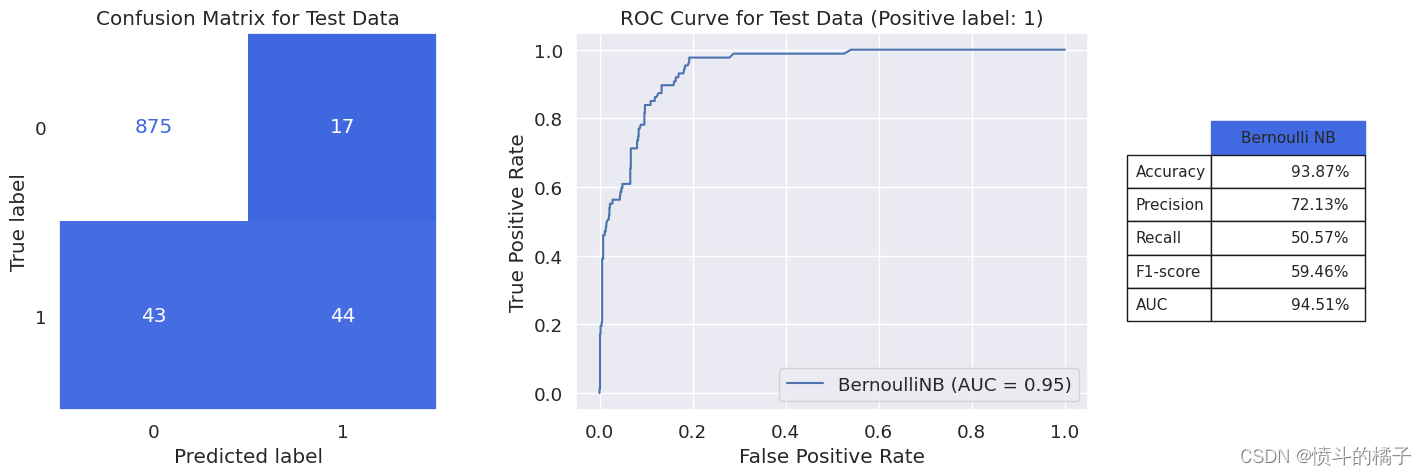
我们相对于补充朴素贝叶斯模型获得了5%的f1-score增加。在伯努利朴素贝叶斯模型中，与补充朴素贝叶斯相比，精确度值增加了，而召回率值减少了。AUC值没有差异。

# 使用Bernoulli Naive Bayes分类器对测试集进行预测，并保存结果
bnb_result = metrics_calculator(bnb, X_test, y_test, 'Bernoulli Naive Bayes')

第十步：逻辑回归模型构建

逻辑回归是一种用于二分类问题的监督式机器学习算法。它将目标变量（通常是二进制）的概率建模为输入特征的函数，使用逻辑函数（sigmoid）将预测映射到0和1之间。该模型使用带标签的数据进行训练，以优化特征的系数以最小化预测误差。

步骤 10.1: 使用标准缩放器对数据进行缩放

在构建逻辑回归分类器之前，我们将对数据应用标准缩放器。

__标准缩放器__用于对数据进行缩放。它通过减去均值并除以标准差来转换数据，确保所有特征具有类似的值范围。

标准缩放对逻辑回归的好处：

1. 梯度下降收敛：逻辑回归中使用的优化算法是梯度下降。当特征具有不同的尺度时，不同特征的梯度大小也会不同。将特征缩放到相同的尺度可以确保所有特征的梯度大小相同，这可以加快优化算法的收敛速度。

2. 正则化：逻辑回归使用正则化来防止过拟合。当特征具有不同的尺度时，成本函数中的正则化项倾向于给具有较高值的特征赋予更大的权重，这在某些情况下可能会导致问题。将特征缩放到相同的尺度可以缓解这个问题。

3. 更好的性能：在某些情况下，对特征进行缩放可以提高逻辑回归模型的性能，特别是当特征具有偏斜分布或不在相同的尺度上时。

# 进行训练集和测试集的划分
# X为特征数据，y为目标数据
# test_size表示测试集所占的比例，这里设置为0.2，即测试集占总数据的20%
# random_state表示随机种子，用于保证每次划分的结果一致，这里设置为0
# stratify表示按照y的分布进行分层抽样，保证训练集和测试集中各类别样本的比例相同
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)

# 创建一个StandardScaler对象
scaler = StandardScaler()

# 使用相同的缩放器对训练数据进行缩放
X_train_scaled = scaler.fit_transform(X_train)

# 使用相同的缩放器对测试数据进行缩放
X_test_scaled = scaler.transform(X_test)

# 将numpy数组转换为pandas数据框，用于训练和测试集
X_train = pd.DataFrame(X_train_scaled, columns=X_train.columns)
X_test = pd.DataFrame(X_test_scaled, columns=X_test.columns)

注意： 非常重要的是，StandardScaler转换应该只从训练集中学习，否则会导致数据泄漏。

步骤 10.2：逻辑回归超参数调优

超参数调优

通过允许逻辑回归模型找到在训练集上产生最低误差的超参数组合，超参数调优可以影响逻辑回归模型的性能。这可以提高预测性能并减少过拟合。然而，如果不进行超参数调优，可能会导致在验证集上过拟合，从而得到一个不能推广到新数据的模型。

另外，由于我们的数据集不平衡，我们打算在优化过程中将少数类别的正确分类比多数类别的正确分类更重要，这被称为对模型进行“惩罚”。我们通过给予少数类别更高的权重来实现这一点。因此，类别的权重也是超参数，在超参数调优过程中确定其最佳值。

步骤 10.2.1：定义超参数网格

超参数网格

超参数网格是指在模型训练过程中预先定义的一组要测试的超参数。每个超参数组合都是网格中的一个单独点，目标是通过在验证集上评估模型性能来选择最佳的超参数。网格定义了超参数优化算法寻找最优超参数的搜索空间。

在逻辑回归中，求解器的选择取决于惩罚项的选择。支持的求解器的惩罚项如下：

• lbfgs -> [ l2 , None ]

• liblinear -> [ l1 , l2 ]

• newton-cg -> [ l2 , None ]

• sag -> [ l2 , None ]

• saga -> [ elasticnet , l1 , l2 , None ]

因此，应考虑不同的求解器和惩罚项的组合。

# 权重与类别相关联的代码
class_weights = [{0:x, 1:1.0-x} for x in np.linspace(0.001,0.5,20)]

# 定义超参数网格
param_grid = [{'solver':['lbfgs', 'newton-cg', 'sag', 'saga'], 
               'penalty':['none'], 
               'class_weight':class_weights}, 
              
              {'solver':['lbfgs', 'newton-cg', 'sag'], 
               'penalty':['l2'], 
               'C': np.logspace(-5, 5, 10), 
               'class_weight':class_weights},
              
              {'solver':['liblinear', 'saga'], 
               'penalty': ['l1', 'l2'], 
               'C': np.logspace(-5, 5, 10), 
               'class_weight':class_weights},
              
              {'solver':['saga'], 
               'penalty':['elasticnet'], 
               'C': np.logspace(-5, 5, 10),
               'l1_ratio': np.arange(0,1.1,0.1), 
               'class_weight':class_weights}] 

# class_weights 是一个列表，其中包含了20个字典，每个字典对应一个权重配置，用于不同类别的权重设置。
# 每个字典中，键0对应类别0的权重，键1对应类别1的权重。

# param_grid 是一个列表，其中包含了4个字典，每个字典对应一个超参数配置。
# 第一个字典中的超参数配置用于solver为'lbfgs', 'newton-cg', 'sag', 'saga'，penalty为'none'的情况。
# 第二个字典中的超参数配置用于solver为'lbfgs', 'newton-cg', 'sag'，penalty为'l2'的情况。
# 第三个字典中的超参数配置用于solver为'liblinear', 'saga'，penalty为'l1', 'l2'的情况。
# 第四个字典中的超参数配置用于solver为'saga'，penalty为'elasticnet'的情况。
# 每个字典中，solver指定了求解器的类型，penalty指定了正则化类型，C指定了正则化强度，class_weight指定了类别权重的配置。
# np.linspace和np.logspace是numpy库中的函数，用于生成等差数列和等比数列。

步骤 10.2.2：寻找最佳超参数

我们使用GridSearchCV来寻找在训练数据上表现最佳的超参数组合。

我们将定义一个函数，该函数将发现模型的最佳__f1-score__值所引起的超参数的最佳组合。出于这个原因，我们定义一个函数，以便将来也可以用来调整超参数。

def tune_clf_hyperparameters(clf, param_grid, X_train, y_train):
    '''
    这个函数通过搜索指定的超参数网格来优化分类器的超参数。它使用GridSearchCV和交叉验证（StratifiedKFold）来评估不同的超参数组合，并选择具有最高f1-score的组合。
    该函数返回具有最佳超参数的最佳分类器。
    '''

    # 使用StratifiedKFold创建交叉验证对象，以确保所有折叠中的类分布相同
    cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=0)

    # 创建GridSearchCV对象
    clf_grid = GridSearchCV(clf, param_grid, cv=cv, scoring=f1_metric, n_jobs=-1)

    # 将GridSearchCV对象拟合到训练数据
    clf_grid.fit(X_train, y_train)

    # 获取最佳超参数
    print("最佳超参数：\n", clf_grid.best_params_)

    # 返回best_estimator_属性，该属性给出了已拟合到训练数据的最佳模型
    return clf_grid.best_estimator_

我们使用上述函数来寻找逻辑回归分类器的最佳超参数组合：

# 定义基础模型
logreg = LogisticRegression(max_iter=1000)

# 调用tune_clf_hyperparameters函数来寻找最佳的超参数组合
logreg_opt = tune_clf_hyperparameters(logreg, param_grid, X_train, y_train)

Best hyperparameters:
 {'C': 3.593813663804626, 'class_weight': {0: 0.4474736842105263, 1: 0.5525263157894738}, 'l1_ratio': 0.2, 'penalty': 'elasticnet', 'solver': 'saga'}

这些是逻辑回归模型的最佳超参数值。logreg_opt是逻辑回归模型，其超参数已设置为最佳值。

步骤 10.3：逻辑回归特征子集选择

让我们来检查每个特征对于我们的逻辑回归模型有多重要。我们使用之前定义的drop_column_importance_plot函数：

drop_column_importance_plot(logreg_opt, X_train, y_train)

几乎没有在“删除列特征重要性”中观察到负值。换句话说，所有特征在目标估计中都是有效的。

步骤 10.4：逻辑回归模型评估

让我们使用model_evaluation函数来评估逻辑回归模型的性能：

model_evaluation(logreg_opt, X_train, X_test, y_train, y_test, 'Logistic Regression')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.97      0.99      0.98      3569
           1       0.81      0.65      0.72       346

    accuracy                           0.96      3915
   macro avg       0.89      0.82      0.85      3915
weighted avg       0.95      0.96      0.95      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.97      0.98      0.97       892
           1       0.72      0.67      0.69        87

    accuracy                           0.95       979
   macro avg       0.85      0.82      0.83       979
weighted avg       0.95      0.95      0.95       979

对比NB伯努利模型，逻辑回归模型的F1得分增加了10%，这是非常好的。

# 保存逻辑回归分类器的最终性能

# 调用metrics_calculator函数，计算逻辑回归分类器的性能指标
# 参数logreg_opt为逻辑回归分类器的优化模型
# 参数X_test为测试集的特征数据
# 参数y_test为测试集的标签数据
# 参数'Logistic Regression'为逻辑回归分类器的名称
# 将计算结果保存在logreg_result变量中
logreg_result = metrics_calculator(logreg_opt, X_test, y_test, 'Logistic Regression')

第11步：KNN模型构建

KNN (K-最近邻) 是一种在机器学习中用于分类和回归问题的监督学习算法。该算法通过找到给定测试样本的K个最近数据点，然后根据K个最近邻中的多数类别对测试样本进行分类。该算法使用距离度量（如欧氏距离）来确定最近的邻居。K的值是一个超参数，决定用于进行预测的邻居数量。

优点：

• 实现和理解简单。
• 不需要训练，它保存训练数据并不需要估计参数。
• 可用于分类和回归问题。

缺点：

• 需要大量内存来存储训练数据。
• 在预测阶段计算量大。
• 在高维数据中效果不好，因为距离度量变得不太有效。
• 可能对多数类别有偏见。
• 对异常值敏感。
• 对不相关特征和噪声数据敏感。进行适当的特征选择很重要。

步骤 11.1：使用标准缩放器对数据进行缩放

由于KNN使用距离度量来找到最近的邻居，因此需要进行标准化（或归一化）以重新调整特征，使它们具有相同的尺度。具有不同尺度和分布的特征可能会影响距离计算并影响算法的性能。

# 导入train_test_split函数用于划分训练集和测试集
from sklearn.model_selection import train_test_split

# 使用train_test_split函数将数据集X和标签y划分为训练集和测试集
# 参数test_size=0.2表示将数据集划分为80%的训练集和20%的测试集
# 参数random_state=0表示设置随机种子，保证每次划分的结果一致
# 参数stratify=y表示按照标签y的分布进行分层划分，保证训练集和测试集中各类别样本的比例相同
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)

# 导入所需的库
import pandas as pd
from sklearn.preprocessing import StandardScaler

# 创建一个StandardScaler对象，用于对训练和测试数据进行缩放
scaler = StandardScaler()

# 使用StandardScaler对象对训练数据进行缩放，并将结果保存在X_train_scaled中
X_train_scaled = scaler.fit_transform(X_train)

# 使用StandardScaler对象对测试数据进行缩放，并将结果保存在X_test_scaled中
X_test_scaled = scaler.transform(X_test)

# 将numpy数组转换为pandas数据框，并将缩放后的训练数据保存在X_train中
X_train = pd.DataFrame(X_train_scaled, columns=X_train.columns)

# 将numpy数组转换为pandas数据框，并将缩放后的测试数据保存在X_test中
X_test = pd.DataFrame(X_test_scaled, columns=X_test.columns)

步骤 11.2: KNN 超参数调整

KNN分类器的超参数如下：

• n_neighbors: 这是用于预测新样本类别的最近邻居的数量。

• weights: 这决定了在进行预测时如何加权样本之间的距离。

  • uniform - 所有邻居的权重相等
  • distance - 距离样本更近的邻居权重更大

• metric: 这是用于确定最近邻居的距离度量。选项有：

  • euclidean
  • manhattan
  • minkowski（两种距离的泛化）

• p: 这是Minkowski度量的幂参数。当p=1时，Minkowski度量等同于曼哈顿距离；当p=2时，等同于欧氏距离。除了1或2之外的p值可以用于以不同方式加权坐标之间的距离的贡献。

我们需要调整knn分类器的超参数值。为此，首先我们定义超参数网格，然后调用tune_clf_hyperparameters函数来找到最佳的超参数组合：

# 定义超参数网格进行搜索
param_grid = [
    {'n_neighbors': np.arange(2, 30), 'metric': ['euclidean','manhattan'], 'weights': ['uniform']},
    {'n_neighbors': np.arange(2, 30), 'metric': ['minkowski'], 'p': [3,4,5], 'weights': ['uniform']}
]

# 第一个字典表示的是一组超参数的取值范围，包括n_neighbors、metric和weights
# n_neighbors的取值范围是从2到29，metric的取值范围是'euclidean'和'manhattan'，weights的取值范围是'uniform'

# 第二个字典表示的是另一组超参数的取值范围，包括n_neighbors、metric、p和weights
# n_neighbors的取值范围是从2到29，metric的取值范围是'minkowski'，p的取值范围是3、4和5，weights的取值范围是'uniform'

让我们调用tune_clf_hyperparameters函数进行超参数调优：

# 导入KNN分类器模型
from sklearn.neighbors import KNeighborsClassifier

# 创建一个KNN分类器对象
knn = KNeighborsClassifier()

# 使用网格搜索方法寻找最佳分类器和最优超参数
knn_opt = tune_clf_hyperparameters(knn, param_grid, X_train, y_train)

Best hyperparameters:
 {'metric': 'minkowski', 'n_neighbors': 3, 'p': 3, 'weights': 'uniform'}

步骤 11.3：KNN 特征子集选择

KNN分类器对无关特征敏感，因为它们在实例之间测量距离并在距离计算中平等地权衡每个特征。这意味着具有高水平的随机性或噪声的特征可能会对计算出的距离产生很大影响，从而导致不准确的预测。

drop_column_importance_plot(knn_opt, X_train, y_train)

在删除列特征重要性输出结果中，观察到了一些具有负重要性的特征。删除这些特征可以提高模型的性能。其中一个具有最负重要性值的特征是邮政编码，我们已经在第3步中意识到，由于其大量的类别，它是一个不重要的特征。
我们对数据集进行过滤：

# 调用 drop_column_importance 函数，计算特征的重要性，并筛选出重要性大于0的特征
feature_importances = drop_column_importance(knn_opt, X_train, y_train, 0)
selected_features = feature_importances[feature_importances['feature importance'] > 0]['feature']

# 根据筛选出的特征，过滤训练集和测试集
X_train = X_train[selected_features]
X_test = X_test[selected_features]

让我们在去除无关特征后再次调整模型的超参数：

# 导入KNN分类器模块
from sklearn.neighbors import KNeighborsClassifier

# 创建一个KNN分类器对象
knn = KNeighborsClassifier()

# 使用网格搜索方法寻找最佳分类器和最优超参数
knn_opt = tune_clf_hyperparameters(knn, param_grid, X_train, y_train)

Best hyperparameters:
 {'metric': 'minkowski', 'n_neighbors': 3, 'p': 5, 'weights': 'uniform'}

第11.4步：KNN模型评估

让我们使用model_evaluation函数评估KNN模型的性能：

model_evaluation(knn_opt, X_train, X_test, y_train, y_test, 'KNN')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      0.99      3569
           1       0.99      0.90      0.94       346

    accuracy                           0.99      3915
   macro avg       0.99      0.95      0.97      3915
weighted avg       0.99      0.99      0.99      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      0.99       892
           1       0.95      0.87      0.91        87

    accuracy                           0.98       979
   macro avg       0.97      0.93      0.95       979
weighted avg       0.98      0.98      0.98       979

我们使用简单的KNN分类器获得了惊人的91%的F1得分，95%的精确度和87%的召回率！

# 调用metrics_calculator函数，计算KNN分类器的性能指标
knn_result = metrics_calculator(knn_opt, X_test, y_test, 'K-Nearest Neighbors')

# 将KNN分类器的性能指标保存起来
knn_result

第12步：SVM模型构建

支持向量机（SVM） 是一种监督学习算法，用于分类或回归任务。它通过找到最佳边界（也称为决策边界）将数据点分成类别，并最大化边界与每个类别的最近数据点（称为支持向量）之间的距离，从而实现分类。SVM可以通过将非线性可分数据转换为高维空间来处理。

优点：

• 对异常值具有鲁棒性： 与其他算法相比，SVM对异常值的敏感性较低，适用于预期存在异常值的任务。

• 多功能性： SVM可用于分类和回归任务，并通过使用核函数处理非线性数据。

• 在高维空间中有效： SVM在高维空间中有效，其中特征数大于样本数。

• 在较小的数据集上表现良好： SVM在较小的数据集上表现良好，不需要大量训练数据即可产生准确的结果。

缺点：

• 在大型数据集上性能较差： 当数据集较大时，SVM可能计算密集且速度较慢。

• 过拟合： SVM可能对数据过拟合，特别是当特征数远大于样本数时。

• 解释能力有限： SVM是一个黑盒模型，很难解释结果并理解算法如何进行预测。

• 选择正确的核函数困难： 核函数的选择对SVM的性能至关重要，但很难确定适用于特定问题的最佳核函数。

步骤 12.1：使用标准缩放器对数据进行缩放

SVM（支持向量机）是一种基于距离的分类器。SVM通过找到最佳边界将数据分成不同的类别，同时最大化边界与每个类别最近数据点（称为支持向量）之间的距离。这意味着SVM基于距离的概念，并寻求找到最优边界以最大化类别之间的距离。因此，在建立模型之前必须进行标准缩放。

# 进行训练集和测试集的划分
# 参数X表示特征数据，y表示目标数据
# test_size表示测试集所占的比例，这里设置为0.2，即测试集占总数据的20%
# random_state表示随机种子，用于保证每次划分的结果一致，这里设置为0
# stratify表示按照目标数据的类别进行分层划分，保证训练集和测试集中各类别的比例相同
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)

# 创建一个StandardScaler对象，用于对数据进行标准化处理
scaler = StandardScaler()

# 对训练数据进行标准化处理，并将结果保存在X_train_scaled中
X_train_scaled = scaler.fit_transform(X_train)

# 对测试数据进行标准化处理，并将结果保存在X_test_scaled中
X_test_scaled = scaler.transform(X_test)

# 将标准化后的训练数据转换为pandas的DataFrame格式，并设置列名为X_train的列名
X_train = pd.DataFrame(X_train_scaled, columns=X_train.columns)

# 将标准化后的测试数据转换为pandas的DataFrame格式，并设置列名为X_test的列名
X_test = pd.DataFrame(X_test_scaled, columns=X_test.columns)

步骤 12.2：SVM 超参数调整

SVM分类器的超参数如下：

• C: 这个超参数控制着在达到低训练误差和低测试误差之间的权衡。C的值越小，边界越宽，误分类的训练样本数量越多；C的值越大，边界越窄，误分类的训练样本数量越少。

• kernel: 这个超参数定义了用于将输入数据转换为高维空间的核函数类型，从而可以找到一个线性边界。常见的核函数包括线性核函数、多项式核函数、径向基函数（rbf）、Sigmoid核函数和预计算核函数。

• gamma: rbf、poly和Sigmoid核函数的核系数。

• degree: 这个超参数只在使用多项式核函数时相关。它定义了用于转换输入数据的多项式函数的次数。

SVM分类器的性能很大程度上受到超参数选择的影响，找到最优的超参数可以帮助提高分类器的性能。因此，我们再次定义超参数网格进行搜索，然后调用tune_clf_hyperparameters函数来找到最适合我们数据的SVM超参数的最优值。

# 定义与类相关的权重
class_weights = [{0:x, 1:1.0-x} for x in np.linspace(0.001,0.5,12)]

# 定义超参数网格进行搜索
param_grid = [
    {
        'kernel': ['poly'],  # 使用多项式核函数
        'degree': [2,3,4,5],  # 多项式核函数的次数
        'gamma': [1, 0.1, 0.01, 0.001, 0.0001],  # 核函数的系数
        'C': [0.01,0.1,1, 10, 100, 1000],  # 惩罚项的系数
        'class_weight': class_weights  # 类别权重
    },
    {
        'kernel': ['rbf','sigmoid'],  # 使用径向基核函数或sigmoid核函数
        'gamma': [1, 0.1, 0.01, 0.001, 0.0001],  # 核函数的系数
        'C': [0.01,0.1,1, 10, 100, 1000],  # 惩罚项的系数
        'class_weight': class_weights  # 类别权重
    },
    {
        'kernel': ['linear'],  # 使用线性核函数
        'C': [0.01,0.1,1, 10, 100, 1000],  # 惩罚项的系数
        'class_weight': class_weights  # 类别权重
    }
]

调整支持向量机（SVM）的超参数可能会耗费大量时间，因为它涉及使用不同的超参数值多次训练模型，并评估它们的性能以找到最佳的超参数组合。在调整了SVM超参数一次后，我们发现rbf核是该数据集的最佳核函数。因此，我们将param_grid限制在rbf核上，以减少程序的运行时间。

# 定义与类相关的权重
class_weights = [{0:x, 1:1.0-x} for x in np.linspace(0.001,0.5,12)]

# 定义要搜索的超参数网格
param_grid = [{'kernel': ['rbf'],
               'gamma': [0.1, 0.01, 0.001, 0.0001], 
               'C': [0.1, 1, 10, 100, 1000],
               'class_weight': class_weights}]

让我们调用tune_clf_hyperparameters函数进行超参数调优：

# 创建一个SVC对象
svm = SVC(probability=True, random_state=0)

# 使用调优前的SVC对象来进行超参数调优
svm_opt = tune_clf_hyperparameters(svm, param_grid, X_train, y_train)

Best hyperparameters:
 {'C': 100, 'class_weight': {0: 0.3639090909090909, 1: 0.636090909090909}, 'gamma': 0.01, 'kernel': 'rbf'}

步骤 12.3: SVM 特征子集选择

SVM分类器对无关特征敏感。如果输入数据包含无关特征，这些特征会对SVM分类器的性能产生负面影响。这是因为SVM算法在寻找决策边界时将所有特征视为同等重要，而无关特征会分散算法对有效分离类别的边界的寻找。

为了避免这个问题，在训练SVM分类器之前建议进行特征选择，即从输入数据中删除任何无关或冗余的特征。这可以通过减少问题的复杂性并允许算法专注于最相关的特征来提高SVM分类器的性能。

drop_column_importance_plot(svm_opt, X_train, y_train)

在删除列特征重要性输出结果中，观察到了几个具有负重要性的特征。删除这些特征可以提高模型的性能。让我们过滤数据集：

# Find Important features with positive feature_importance value
feature_importances = drop_column_importance(svm_opt, X_train, y_train, 0)
selected_features = feature_importances[feature_importances['feature importance']>0.01]['feature']  # Threshold value of 0.01

# Filter dataset
X_train = X_train[selected_features]
X_test = X_test[selected_features]

让我们在去除无关特征后再次调整模型的超参数：

# 创建一个SVC对象
svm = SVC(probability=True, random_state=0)

# 使用给定的参数网格和训练数据来寻找最佳分类器
svm_opt = tune_clf_hyperparameters(svm, param_grid, X_train, y_train)

Best hyperparameters:
 {'C': 1000, 'class_weight': {0: 0.4546363636363636, 1: 0.5453636363636364}, 'gamma': 0.1, 'kernel': 'rbf'}

步骤 12.4：SVM 模型评估

让我们使用model_evaluation函数评估SVM模型的性能：

model_evaluation(svm_opt, X_train, X_test, y_train, y_test, 'SVM')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      1.00      3569
           1       0.97      0.93      0.95       346

    accuracy                           0.99      3915
   macro avg       0.98      0.97      0.97      3915
weighted avg       0.99      0.99      0.99      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      0.99      0.99       892
           1       0.94      0.89      0.91        87

    accuracy                           0.98       979
   macro avg       0.96      0.94      0.95       979
weighted avg       0.98      0.98      0.98       979

我们的SVM模型与KNN模型相比，达到了相同的f1-score，但另一方面，AUC的值已经提高到0.98！

# 使用SVM分类器对测试集进行预测，并计算性能指标
svm_result = metrics_calculator(svm_opt, X_test, y_test, 'SVM')

# 将SVM分类器的最终性能保存起来

第13步：决策树模型构建

优点：

• 易于理解和解释： 决策树简单易懂，可视化效果好。

• 处理数值和分类数据： 决策树可以处理数值和分类数据。

• 特征选择： 决策树可用于特征选择，重要特征会出现在树的根部附近。

• 非参数化： 决策树是非参数化的，意味着它对数据的潜在分布不做任何假设。

缺点：

• 过拟合： 决策树容易过拟合，特别是在深度较大或训练集较小的情况下。这可能导致对新数据的泛化能力较差。

• 不稳定性： 数据的微小变化可能导致树的大幅变化，使决策树不稳定。

• 对具有多个类别的特征有偏好： 决策树对具有多个类别的特征有偏好，因为它们可能会主导树的构建过程。

• 对复杂函数的逼近能力较差： 决策树可能不适合逼近复杂函数，因为它们在每个节点上只能进行轴平行的分割。

注意： 决策树在模型构建之前不需要对数据进行标准缩放。标准缩放通常用于对输入特征的规模敏感的算法，例如基于距离的算法如KNN和SVM。

步骤 13.1: 决策树超参数调优

决策树 分类器容易过拟合。当树过于复杂并且与训练数据过于贴近时，就会发生过拟合，甚至捕捉到数据中的噪声。

防止决策树分类器过拟合的方法:

• 修剪: 删除对分类没有太大贡献的树枝。
• 使用集成方法: 结合多个决策树以获得更强大的模型。
• 限制树的大小: 设置拆分内部节点所需的最小样本数或树的最大深度。

以下是决策树分类器最常见的超参数:

• 准则: 这个超参数确定用于衡量拆分质量的准则。常用的准则有“基尼不纯度”和“信息增益”。

• 最大深度: 这个超参数控制树的最大深度。树越深，变得越复杂，可能导致过拟合。通过设置最大深度可以限制树的大小，从而防止过拟合。

• 每次拆分的最小样本数: 这个超参数设置拆分内部节点所需的最小样本数。如果节点上的样本数小于这个值，节点将无法进一步拆分。这也可以通过限制树的大小来防止过拟合。

• 每个叶节点的最小样本数: 这个超参数设置叶节点所需的最小样本数。如果叶节点的样本数少于这个值，可以将其删除。

• 最大特征数: 这个超参数确定在拆分节点时要考虑的最大特征数。它用于通过减少模型的复杂性来防止过拟合。

• 类别权重: 类别相关的权重。

再次使用上述超参数定义超参数网格，然后调用tune_clf_hyperparameters函数找到最佳组合。

# 定义类别权重
# class_weights是一个列表，其中每个元素是一个字典，字典的键是类别的标签（0或1），值是对应类别的权重
# np.linspace(0.001,1,20)生成一个从0.001到1的等差数列，共有20个元素
# 对于每个权重x，我们将类别0的权重设为x，类别1的权重设为1-x
class_weights = [{0:x, 1:1.0-x} for x in np.linspace(0.001,1,20)]

# 定义超参数网格
# param_grid是一个字典，包含了我们想要调整的超参数及其可能的取值范围
# 'criterion'表示决策树的划分准则，可以是'gini'、'entropy'或'log_loss'
# 'max_depth'表示决策树的最大深度，取值范围是1到9
# 'min_samples_split'表示进行划分所需的最小样本数，取值范围是1到9
# 'min_samples_leaf'表示叶子节点所需的最小样本数，取值范围是1到9
# 'max_features'表示每个节点考虑的特征数，可以是None、'sqrt'或'log2'
# 'class_weight'表示类别权重，取值是之前定义的class_weights列表
param_grid = {'criterion': ['gini', 'entropy', 'log_loss'],
              'max_depth': np.arange(1, 10),
              'min_samples_split': np.arange(1, 10),
              'min_samples_leaf': np.arange(1, 10),
              'max_features': [None, 'sqrt', 'log2'],
              'class_weight': class_weights}

让我们调用tune_clf_hyperparameters函数进行超参数调优：

# 进行训练集和测试集的划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)

# 创建一个决策树分类器对象
dt = DecisionTreeClassifier(random_state=0)

# 使用网格搜索找到最佳的分类器和最优的超参数
dt_opt = tune_clf_hyperparameters(dt, param_grid, X_train, y_train)

Best hyperparameters:
 {'class_weight': {0: 0.6319473684210526, 1: 0.3680526315789474}, 'criterion': 'gini', 'max_depth': 5, 'max_features': None, 'min_samples_leaf': 3, 'min_samples_split': 2}

第13.2步：决策树特征子集选择

特征子集选择对于决策树分类器来说可能很重要。去除冗余或不相关的特征可以通过减少过拟合、增加可解释性和提高计算效率来改善模型的性能。然而，特征子集选择的具体重要性取决于所使用的特定问题和数据集，在某些情况下，决策树模型可以在没有任何特征子集选择的情况下表现良好。

drop_column_importance_plot(dt_opt, X_train, y_train)

在Drop-Column特征重要性方法的输出中，我们观察到一些特征具有负重要性。为了提高模型的性能，我们将删除这些特征：

# 计算决策树模型dt_opt在训练集X_train和标签y_train上的特征重要性，并将结果保存在feature_importances中
feature_importances = drop_column_importance(dt_opt, X_train, y_train, 0)

# 选取特征重要性大于0.01的特征，并将结果保存在selected_features中
selected_features = feature_importances[feature_importances['feature importance']>0.01]['feature']

# 根据选取的特征，过滤训练集和测试集的特征
X_train = X_train[selected_features]
X_test = X_test[selected_features]

让我们在去除无关特征后再次调整模型的超参数：

# 创建一个决策树分类器对象
dt = DecisionTreeClassifier(random_state=0)

# 使用定义的函数来找到具有最佳超参数的决策树分类器
dt_opt = tune_clf_hyperparameters(dt, param_grid, X_train, y_train)

Best hyperparameters:
 {'class_weight': {0: 0.5267894736842105, 1: 0.4732105263157895}, 'criterion': 'gini', 'max_depth': 9, 'max_features': None, 'min_samples_leaf': 6, 'min_samples_split': 2}

步骤 13.3: 决策树模型评估

让我们使用model_evaluation函数来评估我们最终的决策树分类器的性能：

model_evaluation(dt_opt, X_train, X_test, y_train, y_test, 'Decision Tree')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      0.99      3569
           1       0.97      0.90      0.93       346

    accuracy                           0.99      3915
   macro avg       0.98      0.95      0.96      3915
weighted avg       0.99      0.99      0.99      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      0.99       892
           1       0.96      0.86      0.91        87

    accuracy                           0.98       979
   macro avg       0.97      0.93      0.95       979
weighted avg       0.98      0.98      0.98       979

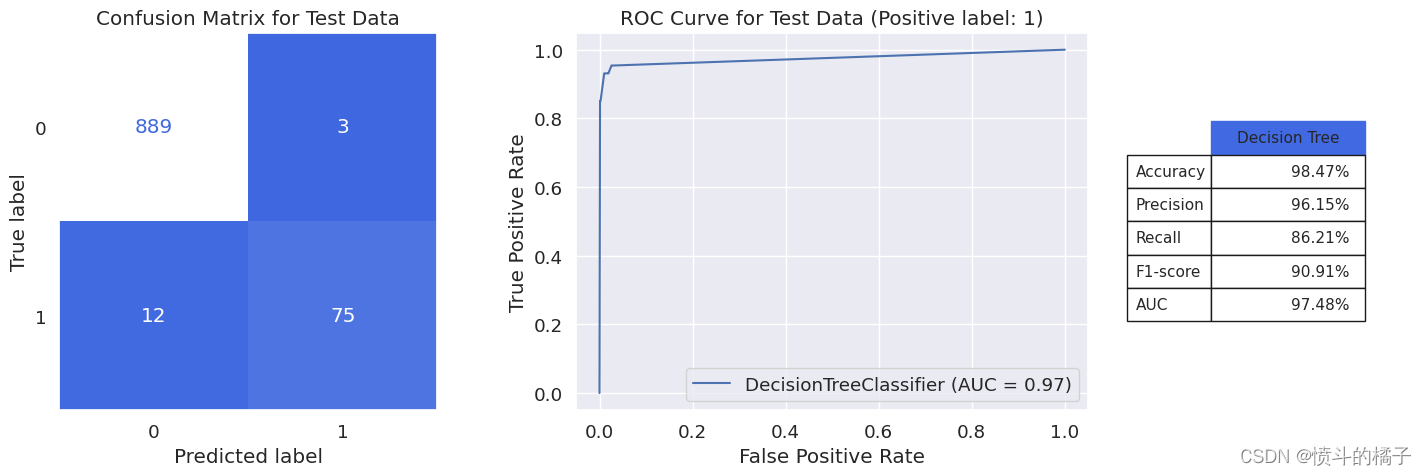
对于决策树分类器，我们得到了91%的F1分数，与之前的两个分类器（KNN和SVM）相似。如果我们检查这些模型的混淆矩阵，在所有3种情况下，FN和FP值的总和都等于15。换句话说，在979名银行客户中，模型在15个案例中出现错误，无法预测客户是否接受贷款。

dt_result = metrics_calculator(dt_opt, X_test, y_test, 'Decision Tree')

第14步：集成学习

集成学习 是一种机器学习技术，它将多个模型的预测结果结合起来，以获得更准确和稳健的预测。集成学习的思想是通过组合多个模型或弱学习器来解决同一个问题，从而使得最终的集成模型比任何单个模型都表现更好。主要有三种集成学习方法：

• Bagging 代表自举聚合。在自举聚合中，同一个基础模型的多个实例被并行地训练在不同的自举样本上，然后通过平均操作来聚合结果。自举聚合最适用于具有低偏差但高方差的基础模型，因为平均操作可以降低最终集成模型的方差。

• Boosting 是一种迭代技术，其中同一个基础模型的多个实例被顺序地训练。在每次迭代中，当前的弱学习器根据前面的弱学习器以及它们在数据上的表现进行训练。Boosting最适用于具有低方差但高偏差的基础模型，因为迭代学习策略可以降低最终集成模型的偏差。

• Stacking 是一种技术，其中不同的基础模型被独立地训练，然后在其之上训练一个元模型来根据基础模型的输出预测结果。在堆叠中，基础模型被用作元模型的特征，最终的预测结果基于所有基础模型的组合信息。

决策树经常被用作集成方法中的基本模型，因为它们具有以下几个特点，使其非常适合这个目的：

1. 简单易懂： 决策树简单易懂，这使得它们成为集成方法中作为基本模型的良好选择。

2. 处理非线性关系： 决策树可以处理特征和目标变量之间的非线性关系，这使得它们成为建模复杂数据集的良好选择。

3. 处理缺失值和异常值： 决策树能够处理数据中的缺失值和异常值，这对于现实世界中经常出现这些问题的数据集非常重要。

4. 能够捕捉特征之间的交互作用： 决策树能够捕捉特征之间的交互作用，这对于捕捉数据中的复杂关系非常重要。

5. 训练和预测速度快： 决策树的训练和预测速度快，这使得它们非常适合在大规模机器学习模型中使用。

6. 提供特征重要性： 决策树提供特征重要性，这对于理解哪些特征对模型的预测贡献最大非常有用。

基于决策树分类器的最重要的装袋模型有：

• 随机森林（Random Forest）： 随机森林是一种集成学习方法，它使用决策树作为基本模型。随机森林中的树是在训练数据的自助样本和随机选择的特征子集上生长的。这有助于减少树之间的相关性，并使模型对缺失数据更加稳健。随机森林的目标是通过组合多个深度决策树来降低模型的方差。装袋和随机特征子空间选择的组合相比单个决策树可以得到更稳健和准确的模型。

• 极端随机树（Extra Trees）： 极端随机树是随机森林的扩展，它使用随机分割而不是基于信息增益或其他准则来优化分割。这使得极端随机树的训练速度比随机森林更快，并且更不容易过拟合。

最重要的提升模型有：

• Adaboost： 这是最早和最流行的提升算法之一。它训练一系列弱决策树，并在每次迭代中给误分类样本分配更大的权重。

• 梯度提升（Gradient Boosting）： 这是一种通用的提升算法，适用于各种弱模型，包括决策树。它使用梯度下降优化方法来最小化损失函数，并找到最佳的弱模型组合。

• XGBoost： 这是梯度提升的优化实现，也是机器学习社区中最广泛使用的算法之一。它以其快速的训练速度、可扩展性和处理大型数据集的能力而闻名。

• LightGBM： 这是另一种经过优化的梯度提升实现，专为大型数据集设计，并在工业界得到广泛应用。

步骤15：随机森林模型构建

随机森林 是一种集成学习方法，用于分类、回归和其他任务。它在训练时通过构建多个决策树，并输出类别的众数（分类）或平均预测值（回归）来进行操作。随机森林中的树是从训练数据的随机选择样本和特征的子集中生长出来的。通过结合多个树，它减少了过拟合并提高了稳定性，因此得名"森林"。

第15.1步：随机森林超参数调整

调整随机森林分类器的超参数可以提高其在给定问题上的性能。超参数控制模型的复杂性和行为，它们的值对模型的准确性和泛化能力有重要影响。例如，将树的最大深度设置得太高可能导致过拟合，而将其设置得太低可能导致欠拟合。对于其他超参数，如分裂节点所需的最小样本数或分裂节点时考虑的特征数，也是如此。调整超参数有助于找到在解决特定问题时性能最佳的值组合。

随机森林分类器的超参数包括：

• n_estimators: 森林中树的数量。

• criterion: 用于衡量分裂质量的函数。常见的准则包括基尼不纯度和信息增益。

• max_depth: 树的最大深度。这可以用来控制模型的复杂性并防止过拟合。

• min_samples_split: 分裂内部节点所需的最小样本数。

• min_samples_leaf: 叶节点所需的最小样本数。

• bootstrap: 构建森林时是否使用替换采样。

• oob_score: 是否使用袋外样本来估计泛化准确性。

• class_weight: 类别相关的权重。

• max_features: 分裂节点时考虑的最大特征数。可以设置为一个数字、一个浮点数（百分比）或’sqrt’或’log2’。

我们为我们的随机森林分类器设置了每个超参数的取值范围，然后使用tune_clf_hyperparameters函数来找到提供最佳结果的超参数组合。

注意： 构成森林的树可以是 浅层 的，意味着它们具有有限的分支或层级，也可以是 深层 的，意味着它们具有许多分支或层级，并且尚未完全生长。 深层树 具有 低偏差 但 高方差，因此是 减少方差 的 装袋方法 的相关选择。在选择随机森林超参数的取值范围时，我们考虑使用深层树。

# 定义类别权重
class_weights = [{0:x, 1:1.0-x} for x in np.linspace(0.001,1,20)]
# 这里使用np.linspace函数生成一个包含20个元素的数组，从0.001到1之间均匀分布的数值，作为类别权重的参数x
# 对于每个x，创建一个字典，字典的键是类别0和类别1，对应的值是权重1-x和x

# 定义超参数网格进行搜索
param_grid = {
    'n_estimators': [50, 100, 150],  # 决策树的数量
    'max_depth': np.arange(5, 12),  # 决策树的最大深度范围
    'min_samples_split': [1, 2, 3],  # 内部节点再划分所需的最小样本数
    'min_samples_leaf': [1, 2, 3],  # 叶子节点所需的最小样本数
    'class_weight': class_weights  # 类别权重
}
# 这里定义了一个字典param_grid，包含了多个超参数的取值范围
# 'n_estimators'表示决策树的数量，取值范围为[50, 100, 150]
# 'max_depth'表示决策树的最大深度，取值范围为从5到11的整数
# 'min_samples_split'表示内部节点再划分所需的最小样本数，取值范围为[1, 2, 3]
# 'min_samples_leaf'表示叶子节点所需的最小样本数，取值范围为[1, 2, 3]
# 'class_weight'表示类别权重，取值为之前定义的class_weights列表中的元素

让我们调用tune_clf_hyperparameters函数来进行超参数调优：

# 进行训练集和测试集的划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)

# 创建一个随机森林分类器对象
rf = RandomForestClassifier(criterion='gini', max_features=None, bootstrap=True, random_state=0)

# 使用给定的参数网格对分类器进行超参数调优，找到最佳分类器
rf_opt = tune_clf_hyperparameters(rf, param_grid, X_train, y_train)

Best hyperparameters:
 {'class_weight': {0: 0.5793684210526315, 1: 0.42063157894736847}, 'max_depth': 9, 'min_samples_leaf': 2, 'min_samples_split': 2, 'n_estimators': 100}

步骤 15.2：随机森林特征子集选择

特征选择对于随机森林分类器非常重要，因为它有助于提高模型的性能，减少过拟合，并通过从数据中删除不相关、冗余或噪声特征来加快训练时间。让我们调用drop_column_importance_plot函数：

drop_column_importance_plot(rf_opt, X_train, y_train)

特征重要性中没有观察到负值。因此，所有特征在估计目标值时都是有效的，没有被认为是有害或冗余的。

步骤 15.3：随机森林模型评估

让我们使用model_evaluation函数评估我们的最佳随机森林分类器的性能：

model_evaluation(rf_opt, X_train, X_test, y_train, y_test, 'Primary RF')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       1.00      1.00      1.00      3569
           1       1.00      0.95      0.97       346

    accuracy                           1.00      3915
   macro avg       1.00      0.98      0.99      3915
weighted avg       1.00      1.00      1.00      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      0.99       892
           1       0.96      0.89      0.92        87

    accuracy                           0.99       979
   macro avg       0.98      0.94      0.96       979
weighted avg       0.99      0.99      0.99       979

如果我们比较训练集和测试集上类别1（更重要的类别）的精确度、召回率和F1分数的值，我们会发现测试数据集上的分数略微低于训练数据集，这表明模型存在一定的过拟合现象。
模型的过拟合是由于其高方差造成的，在接下来的过程中，我们尝试通过对超参数的微小调整来减轻模型的过拟合，希望模型在测试数据上的性能会有所提升。

这些随机森林分类器超参数如何增加模型的方差？

• n_estimators - 增加森林中的树的数量将增加方差，因为森林中的更多树可以捕捉数据中更多不同的模式。

• max_depth - 增加树的最大深度可以捕捉数据中更复杂的模式，增加方差。

• min_samples_split - 减少分割内部节点所需的最小样本数将增加方差，因为它允许更多的分割发生。

• min_samples_leaf - 减少要求在叶节点上的最小样本数将增加方差，因为它允许形成更小的叶子。

• max_features - 增加在分割节点时考虑的最大特征数将增加方差，因为它允许考虑更多不同的特征集进行分割。

• bootstrap - 在构建森林中的树时进行有放回抽样将增加方差，因为它允许每棵树使用更多不同的样本集。

在获得的超参数的最优值中，我们只将__min_samples_leaf__的值从2增加到6，以部分减小模型的方差。

# 导入随机森林分类器模型
from sklearn.ensemble import RandomForestClassifier

# 使用得到的超参数的最优值构建随机森林分类器对象
rf_final = RandomForestClassifier(criterion='gini', max_features=None, bootstrap=True, n_estimators=100, 
                                  max_depth=9, min_samples_leaf=6, min_samples_split=2,
                                  class_weight={0: 0.58, 1: 0.42}, random_state=0)

# 使用训练集数据对最终的随机森林模型进行训练
rf_final.fit(X_train, y_train)

RandomForestClassifier(class_weight={0: 0.58, 1: 0.42}, max_depth=9,
                       max_features=None, min_samples_leaf=6, random_state=0)

让我们再次评估我们的随机森林分类器：

model_evaluation(rf_final, X_train, X_test, y_train, y_test, 'Random Forest')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      0.99      3569
           1       0.99      0.90      0.94       346

    accuracy                           0.99      3915
   macro avg       0.99      0.95      0.97      3915
weighted avg       0.99      0.99      0.99      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      0.99       892
           1       0.99      0.90      0.94        87

    accuracy                           0.99       979
   macro avg       0.99      0.95      0.97       979
weighted avg       0.99      0.99      0.99       979

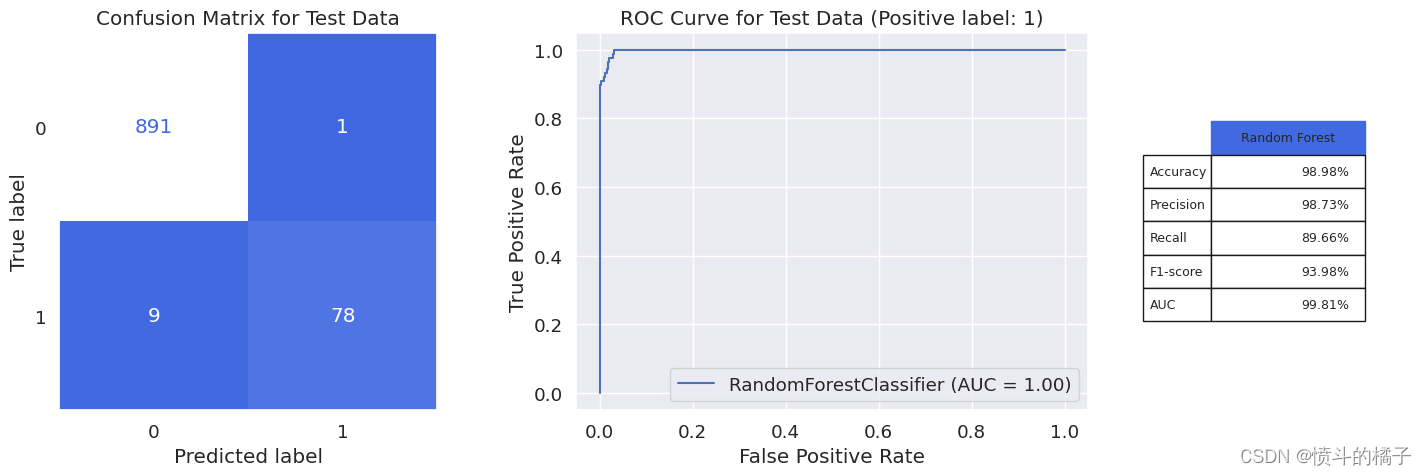
我们的随机森林分类器取得了94%的显著f1分数和99.81%的AUC。在979名银行客户中，该模型仅在10个案例中出现错误，预测客户是否接受贷款。

# 使用Random Forest分类器对测试集进行预测，并保存结果
rf_result = metrics_calculator(rf_final, X_test, y_test, 'Random Forest')

步骤16：构建Extra Trees模型

极端随机树（Extra Trees） 是一种用于分类和回归问题的集成学习方法。它是流行的随机森林算法的一种变体，利用随机化构建决策树来创建一片树林。

在 随机森林 中，集成中的每棵树都是使用特征的随机子集和训练样本的随机子集构建的。最终的预测是通过对集成中所有树的预测取平均值（用于回归）或多数表决（用于分类）来进行的。但是在极端随机树分类器中，集成中的每棵树都是使用训练样本的随机子集构建的，并且对于每个特征使用一个随机阈值来分割样本。这意味着与随机森林相比，极端随机树分类器在树的构建过程中允许更多的随机性，这使得它更适用于某些类型的数据集。

两者之间的另一个区别是，与随机森林相比，极端随机树分类器往往具有稍高的方差，这意味着它更容易过拟合训练数据。然而，这种较高的方差也可能导致在某些数据集上表现更好，使得极端随机树成为某些情况下值得考虑的有用替代方案。

步骤 16.1：Extra Trees 超参数调整

超参数的Extra Trees分类器与随机森林类似。因此，我们再次设置每个超参数的值范围，以便我们考虑我们的Extra Trees分类器，并使用tune_clf_hyperparameters函数来找到提供最佳结果的超参数组合。

注意： 调整随机森林超参数可能会耗费时间。这是因为找到超参数的最佳值涉及训练多个具有不同超参数值组合的决策树分类器，并评估它们的性能，这可能会耗费计算资源和时间。因此，我们进行了一次超参数调整，然后在以下param_grid中缩小了超参数值的范围。

# 定义类别权重
class_weights = [{0:x, 1:1.0-x} for x in np.linspace(0.001,1,20)]

# 定义超参数网格进行搜索
param_grid = {
    'n_estimators': [70, 100, 150],  # 决策树的数量
    'max_depth': [10,12,14],  # 决策树的最大深度
    'min_samples_split': [1,2,3],  # 内部节点再划分所需的最小样本数
    'min_samples_leaf': [1,2,3],  # 叶子节点最少样本数
    'class_weight': class_weights  # 类别权重
}

让我们调用tune_clf_hyperparameters函数进行超参数调优：

from sklearn.ensemble import ExtraTreesClassifier

# 对数据进行训练集和测试集的划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)

# 创建一个随机森林分类器对象
et = ExtraTreesClassifier(criterion='gini', max_features=None, bootstrap=True, random_state=0)

# 使用给定的参数网格对分类器进行超参数调优，找到最佳的分类器
et_opt = tune_clf_hyperparameters(et, param_grid, X_train, y_train)

Best hyperparameters:
 {'class_weight': {0: 0.9474210526315789, 1: 0.05257894736842106}, 'max_depth': 14, 'min_samples_leaf': 1, 'min_samples_split': 2, 'n_estimators': 70}

步骤 16.2：额外树特征子集选择

特征选择对于Extra Trees分类器同样重要。特征选择有助于减少数据集的维度，并选择一组与模型预测性能最有影响的相关特征子集。这可以提高模型的可解释性，减少过拟合，并加快训练时间。然而，特征选择对于Extra Trees分类器的重要性可能因特定数据集和问题的解决而异。在模型性能上实验和评估特征选择的影响是一种良好的实践。

drop_column_importance_plot(et_opt, X_train, y_train)

再次观察，删除列特征重要性中没有观察到负值。因此，所有特征在估计目标值时都是有效的，没有被认为是多余的。

第16.3步：额外树模型评估

让我们使用model_evaluation函数评估我们的最佳Extra Trees分类器的性能：

model_evaluation(et_opt, X_train, X_test, y_train, y_test, 'Primary Extra Trees')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       1.00      1.00      1.00      3569
           1       1.00      1.00      1.00       346

    accuracy                           1.00      3915
   macro avg       1.00      1.00      1.00      3915
weighted avg       1.00      1.00      1.00      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      0.99       892
           1       0.98      0.92      0.95        87

    accuracy                           0.99       979
   macro avg       0.98      0.96      0.97       979
weighted avg       0.99      0.99      0.99       979

模型过拟合的比较

对于训练集和测试集中类别1的精确度、召回率和F1分数的比较表明，该模型存在轻微的过拟合现象。如果类别1在测试集上的性能与训练集相比显著下降，这表明模型对训练数据学习得太好，对新的未知数据泛化能力不强。这种过拟合导致测试集上的性能较差，并且表明该模型不适合对新数据进行准确的预测。

根据第15.3节中给出的解释，通过将min_samples_leaf的值从2增加到3，模型变得更简单，模型的方差减小了：

# 使用得到的超参数值构建Extra Trees分类器对象
et_final = ExtraTreesClassifier(criterion='gini', max_features=None, bootstrap=True, n_estimators=70, 
                                max_depth=14, min_samples_leaf=1, min_samples_split=3,
                                class_weight={0: 0.95, 1: 0.05}, random_state=0)

# 使用训练集数据对最终的Extra Trees模型进行训练
et_final.fit(X_train, y_train)

ExtraTreesClassifier(bootstrap=True, class_weight={0: 0.95, 1: 0.05},
                     max_depth=14, max_features=None, min_samples_split=3,
                     n_estimators=70, random_state=0)

让我们再次评估我们的Extra Trees分类器：

model_evaluation(et_final, X_train, X_test, y_train, y_test, 'Extra Trees')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       1.00      1.00      1.00      3569
           1       1.00      0.96      0.98       346

    accuracy                           1.00      3915
   macro avg       1.00      0.98      0.99      3915
weighted avg       1.00      1.00      1.00      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      1.00       892
           1       0.99      0.92      0.95        87

    accuracy                           0.99       979
   macro avg       0.99      0.96      0.97       979
weighted avg       0.99      0.99      0.99       979

如图所示，该模型不再过拟合，并且与先前的模型相比，在测试数据上的模型性能有所提高。我们的Extra Trees分类器取得了惊人的95%的f1-score和99.84%的AUC，这是我们迄今为止最好的分类器。在979名银行客户中，该模型仅在8个案例中出现错误，以预测客户是否接受贷款。

et_result = metrics_calculator(et_final, X_test, y_test, 'Extra Trees')

第17步：AdaBoost模型构建

AdaBoost（自适应增强） 是一种常用的提升集成学习算法，用于分类和回归任务。它将多个“弱”分类器组合起来，创建一个强分类器，以进行准确的预测。弱分类器逐个进行训练，算法根据它们的误分类率调整训练实例的权重。AdaBoost的思想是专注于之前弱分类器误分类的样本，以便后续的弱分类器能够更好地对这些样本进行分类。通过结合多个弱分类器的输出，算法试图提高分类器的整体准确性。

术语“弱分类器”指的是一个简单的分类器，它的准确性不高，但与其他弱分类器结合时，会产生一个强大的整体分类器。通常，在AdaBoost中使用决策树作为弱分类器。然而，任何接受训练数据权重的机器学习算法都可以作为AdaBoost中的基学习器。

步骤 17.1: AdaBoost 超参数调整

AdaBoost分类器的超参数包括：

• 学习率： 此参数确定每个弱学习器在最终预测中的贡献。较低的学习率会导致较慢的收敛，但预测更准确。

• 估计器数量： 这是用于创建最终强分类器的弱学习器的最大数量。更多的估计器可以导致更准确的预测，但也会增加计算时间。

• 估计器： 用于弱学习器的算法可以根据手头的问题进行选择。我们选择决策树。

注意： 除了AdaBoost分类器的超参数，如学习率、估计器数量和采样策略之外，基本估计器的超参数也需要进行优化，以达到最佳性能。浅树具有高偏差但低方差，因此是主要关注减少偏差的提升方法的相关选择。浅树允许提升算法专注于难以分类的样本。

我们为AdaBoost分类器设置了每个超参数的取值范围，然后使用tune_clf_hyperparameters函数来找到提供最佳结果的超参数组合。

# 定义AdaBoost的超参数网格
ada_param_grid = {
    'base_estimator__max_depth': [3, 5, 7],  # 基础估计器的最大深度参数的取值范围
    'base_estimator__min_samples_split': [3, 5, 7],  # 基础估计器的最小样本分割参数的取值范围
    'base_estimator__min_samples_leaf': [1, 2, 3],  # 基础估计器的最小叶子节点样本数参数的取值范围
    'n_estimators': [50, 100, 150],  # AdaBoost中基础估计器的数量参数的取值范围
    'learning_rate': [0.8, 0.9, 1]  # AdaBoost中学习率参数的取值范围
}

让我们调用tune_clf_hyperparameters函数进行超参数调优：

# 导入必要的库
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier

# 执行训练集和测试集的划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)

# 创建决策树分类器作为基础估计器
dt = DecisionTreeClassifier(criterion='gini', max_features=None, random_state=0)

# 使用决策树作为基础估计器创建AdaBoost分类器
ada = AdaBoostClassifier(base_estimator=dt, random_state=0)

# 使用给定的超参数网格搜索找到最佳的AdaBoost分类器
ada_opt = tune_clf_hyperparameters(ada, ada_param_grid, X_train, y_train)

Best hyperparameters:
 {'base_estimator__max_depth': 5, 'base_estimator__min_samples_leaf': 2, 'base_estimator__min_samples_split': 5, 'learning_rate': 0.9, 'n_estimators': 100}

步骤 17.2：AdaBoost 特征子集选择

特征选择对于AdaBoost分类器来说非常重要。特征选择有助于减少数据的维度，降低计算成本，并防止过拟合。此外，它可以通过关注最相关的特征来提高模型的可解释性和分类器的准确性。然而，特征选择对于AdaBoost分类器的具体影响可能因问题和数据的不同而异。

drop_column_importance_plot(ada_opt, X_train, y_train)

结果的特征重要性分析显示，所有特征的删除列重要性都没有负值。这表明所有特征对目标的估计都有积极的贡献，没有一个特征可以被认为是不必要或多余的。所有特征都被认为对目标的预测是有效的。

步骤 17.3：AdaBoost 模型评估

让我们使用model_evaluation函数评估我们的最佳AdaBoost分类器的性能：

model_evaluation(ada_opt, X_train, X_test, y_train, y_test, 'Primary AdaBoost')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       1.00      1.00      1.00      3569
           1       1.00      1.00      1.00       346

    accuracy                           1.00      3915
   macro avg       1.00      1.00      1.00      3915
weighted avg       1.00      1.00      1.00      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      0.99      0.99       892
           1       0.94      0.91      0.92        87

    accuracy                           0.99       979
   macro avg       0.97      0.95      0.96       979
weighted avg       0.99      0.99      0.99       979

性能指标

在测试数据上，针对少数类别的性能指标显示模型并没有完全过拟合，但可能不是问题的最佳模型。分类器的过拟合是由于其高方差引起的，为了避免过拟合，我们可以尝试正则化技术，即对超参数的值进行微小改变以减少分类器的方差。

如何通过调整模型超参数来减少AdaBoost分类器的方差？

• 减少模型中的树的数量： AdaBoost使用多个弱学习器（在本例中为决策树）来构建一个强模型。减少模型中的树的数量可以减少模型的方差。

• 减少决策树的最大深度： 减少决策树的最大深度可以减少模型的方差。

• 增加分裂内部节点所需的最小样本数： 增加分裂内部节点所需的最小样本数可以减少模型的方差。

• 增加叶节点所需的最小样本数： 增加叶节点所需的最小样本数可以减少模型的方差。

• 减小学习率： AdaBoost中的学习率决定了每个弱学习器所赋予的权重。减小学习率可以使模型更不容易过拟合。

在获得的超参数的最优值中，我们只将学习率的值从0.9降低到0.8，以部分减少模型的方差。

# 导入需要的库
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier

# 创建决策树分类器作为基本估计器
dt = DecisionTreeClassifier(criterion='gini', max_features=None, random_state=0, max_depth=5, min_samples_leaf=2, min_samples_split=5)

# 使用决策树作为基本估计器创建AdaBoost分类器
ada_final = AdaBoostClassifier(base_estimator=dt, random_state=0, learning_rate=0.8, n_estimators=100)

# 训练最终的AdaBoost分类器
ada_final.fit(X_train, y_train)

AdaBoostClassifier(base_estimator=DecisionTreeClassifier(max_depth=5,
                                                         min_samples_leaf=2,
                                                         min_samples_split=5,
                                                         random_state=0),
                   learning_rate=0.8, n_estimators=100, random_state=0)

让我们评估我们的最终AdaBoost分类器：

model_evaluation(ada_final, X_train, X_test, y_train, y_test, 'AdaBoost')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       1.00      1.00      1.00      3569
           1       1.00      1.00      1.00       346

    accuracy                           1.00      3915
   macro avg       1.00      1.00      1.00      3915
weighted avg       1.00      1.00      1.00      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      0.99       892
           1       0.96      0.92      0.94        87

    accuracy                           0.99       979
   macro avg       0.98      0.96      0.97       979
weighted avg       0.99      0.99      0.99       979

模型的方差减小，从而提高了模型在测试数据上的性能。由于测试数据和训练数据的分数差异不大且AUC分数较高，我们可以忽略它。在测试数据上获得的f1-score与先前的bagging模型几乎相同。

注意: AUC (曲线下面积) 指标通过绘制真正例率与假正例率的曲线并计算曲线下面积来衡量二元分类器的性能。一个没有过拟合的模型将具有较高的AUC，接近1，表明它在真正例和假正例预测之间具有良好的平衡。另一方面，一个过拟合的模型可能在训练集上具有较高的准确性，但在验证集上具有较低的AUC，因为它可能会进行许多错误的正例预测。因此，高AUC分数表明模型没有过拟合，并且在新的、未见过的数据上具有良好的泛化性能。

# 使用AdaBoost分类器对测试数据进行预测，并计算性能指标
ada_result = metrics_calculator(ada_final, X_test, y_test, 'AdaBoost')

# 将AdaBoost分类器的最终性能保存起来

第18步：梯度提升模型构建

梯度提升 是一种用于分类和回归问题的集成机器学习技术，它以一组弱预测模型（通常是决策树）的集合形式生成预测模型。它以逐阶段的方式构建模型，每个后续模型都试图纠正前一个模型的错误。该算法迭代地训练决策树，使得树能够适应被优化的损失函数的负梯度。最终的预测是通过组合所有个体树的输出来进行的。

注意： scikit-learn的集成模块（sklearn.ensemble.GradientBoostingClassifier）中的梯度提升分类器的实现是基于决策树作为基本估计器。

步骤18.1：梯度提升超参数调整

Gradient Boosting分类器的超参数包括：

• n_estimators: 集成中树的数量。

• learning_rate: 学习率通过学习率因子来缩小每棵树的贡献。它是一个控制更新幅度的参数，对于大量的树应该设置较低的值。

• max_depth: 每棵决策树的最大深度。树越深，划分越多，模型越复杂。

• min_samples_split: 划分内部节点所需的最小样本数。

• min_samples_leaf: 叶节点所需的最小样本数。

• max_features: 在寻找最佳划分时要考虑的特征数量。

• subsample: 用于拟合个体基学习器的样本比例。

• loss: 要优化的损失函数。默认的损失函数是“偏差”，用于二元分类的逻辑回归和多类分类问题的多项偏差。

• criterion: 用于衡量划分质量的函数。支持的标准有“friedman_mse”用于均方误差，用于回归问题，“entropy”或“gini”用于信息增益，用于分类问题。

我们再次设置每个超参数的取值范围，以便考虑我们的梯度提升分类器所需的最佳超参数组合，并使用tune_clf_hyperparameters函数来找到提供最佳结果的超参数组合。

# 定义超参数网格用于调优
gbc_param_grid = {
    'n_estimators': [50, 100, 200, 300, 400, 500],  # 决策树的数量
    'max_depth': [1, 2, 3, 4, 5],  # 决策树的最大深度
    'min_samples_split': [2, 4, 6, 8, 10],  # 分裂内部节点所需的最小样本数
    'min_samples_leaf': [1, 2, 3, 4, 5],  # 叶子节点所需的最小样本数
    'max_features': [None, 'sqrt', 'log2'],  # 最大特征数
    'loss': ['deviance', 'exponential'],  # 损失函数
    'criterion': ['friedman_mse', 'squared_error'],  # 分裂质量的度量标准
    'subsample': [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],  # 每棵树使用的样本比例
    'learning_rate': [0.01, 0.05, 0.1, 0.2, 0.3]  # 学习率
}

由于上述网格上的超参数调整可能非常耗时，因为网格的大小很大，所以在一次执行并知道最佳值后，我们会将网格值集合变小：

# 定义超参数网格用于调优
gbc_param_grid = {
    'n_estimators': [50, 100, 150],  # 决策树的数量
    'max_depth': [4, 5, 6],  # 决策树的最大深度
    'min_samples_split': [2, 3],  # 分裂内部节点所需的最小样本数
    'min_samples_leaf': [3, 4, 5],  # 叶子节点所需的最小样本数
    'subsample': [0.9, 1.0],  # 每棵树使用的样本比例
    'learning_rate': [0.3, 0.4, 0.5]  # 学习率
}

让我们调用tune_clf_hyperparameters函数进行超参数调优：

# 进行训练集和测试集的划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)

# 初始化梯度提升分类器
gbc = GradientBoostingClassifier(max_features=None, loss='deviance', criterion='friedman_mse', random_state=0)

# 从调参过程中找到最佳的超参数
gbc_opt = tune_clf_hyperparameters(gbc, gbc_param_grid, X_train, y_train)

Best hyperparameters:
 {'learning_rate': 0.4, 'max_depth': 5, 'min_samples_leaf': 4, 'min_samples_split': 2, 'n_estimators': 100, 'subsample': 1.0}

第18.2步：梯度提升特征子集选择

特征选择对梯度提升分类器的具体影响因问题和数据而异。在某些情况下，梯度提升算法可以处理大量特征而不会显著降低性能，但在其他情况下，特征选择仍然是有益的。

drop_column_importance_plot(gbc_opt, X_train, y_train)

特征重要性分析显示，每个特征对于预测目标都有积极的影响，意味着它们中没有一个有负面影响。

第18.3步：梯度提升模型评估

让我们使用model_evaluation函数评估我们的最佳梯度提升分类器的性能：

model_evaluation(gbc_opt, X_train, X_test, y_train, y_test, 'Primary Grad. Boosting')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       1.00      1.00      1.00      3569
           1       1.00      1.00      1.00       346

    accuracy                           1.00      3915
   macro avg       1.00      1.00      1.00      3915
weighted avg       1.00      1.00      1.00      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      0.99      0.99       892
           1       0.94      0.92      0.93        87

    accuracy                           0.99       979
   macro avg       0.97      0.96      0.96       979
weighted avg       0.99      0.99      0.99       979

我们的梯度提升分类器在少数类上有一定的过拟合。因此，我们需要通过略微改变超参数的值来减小分类器的方差。

如何通过调整模型超参数来减少梯度提升分类器的方差？

• 树的数量： 我们可以减少树的数量来降低模型的方差。更多的树意味着更复杂的模型，更容易过拟合。

• 树的最大深度： 我们可以减少模型中树的最大深度，通过限制分裂的次数来降低模型的方差。

• 学习率： 降低学习率会减小模型参数的更新幅度，使模型更难过拟合训练数据。

• 子采样： 在模型训练的每次迭代中，可以通过对训练数据进行较小的采样来防止过拟合，从而引入随机性到模型中。

• 树特定的超参数： 通过调整决策树特定的超参数，可以降低模型的方差。例如，我们可以增加分裂节点所需的最小样本数或叶子节点中的最小样本数。

在获得的超参数的最优值中，我们只将学习率的值从0.4降低到0.2，以部分减少模型的方差。

# 导入Gradient Boosting Classifier模型
from sklearn.ensemble import GradientBoostingClassifier

# 初始化Gradient Boosting Classifier模型
# max_features=None表示使用所有特征
# loss='deviance'表示使用对数似然损失函数
# criterion='friedman_mse'表示使用Friedman均方误差作为划分标准
# learning_rate=0.2表示学习率为0.2
# max_depth=5表示决策树的最大深度为5
# n_estimators=100表示使用100个弱分类器
# subsample=1.0表示使用全部样本进行训练
# min_samples_leaf=4表示叶子节点最少包含4个样本
# min_samples_split=2表示内部节点划分所需的最小样本数为2
# random_state=0表示随机种子为0，保证结果可复现
gbc_final = GradientBoostingClassifier(max_features=None, loss='deviance', criterion='friedman_mse',
                                 learning_rate=0.2, max_depth=5, n_estimators=100, subsample=1.0,
                                 min_samples_leaf=4, min_samples_split=2, random_state=0)

# 使用训练集数据进行训练
gbc_final.fit(X_train, y_train)

GradientBoostingClassifier(learning_rate=0.2, max_depth=5, min_samples_leaf=4,
                           random_state=0)

让我们评估我们最终的梯度提升分类器：

model_evaluation(gbc_final, X_train, X_test, y_train, y_test, 'Gradient Boosting')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       1.00      1.00      1.00      3569
           1       1.00      1.00      1.00       346

    accuracy                           1.00      3915
   macro avg       1.00      1.00      1.00      3915
weighted avg       1.00      1.00      1.00      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      1.00       892
           1       0.99      0.92      0.95        87

    accuracy                           0.99       979
   macro avg       0.99      0.96      0.97       979
weighted avg       0.99      0.99      0.99       979

模型的方差被降低，因此我们的梯度提升分类器取得了令人瞩目的95.24%的f1-score和99.92%的AUC，这是目前所有分类器中表现最好的。在979名银行客户中，该模型仅在8个案例中出现错误，预测客户是否接受贷款。现在让我们揭开我们的终极武器：XGBoost分类器！

gbc_result = metrics_calculator(gbc_final, X_test, y_test, 'Gradient Boosting')

第19步：XGBoost模型构建

XGBoost

XGBoost 是一种基于树的机器学习模型的梯度提升算法。它代表着 eXtreme Gradient Boosting。XGBoost 是梯度提升的高度优化实现，旨在快速且内存高效。

与其他梯度提升实现相比，XGBoost 具有以下几个独特的特点：

• 处理缺失值
• 并行处理训练和预测
• 树剪枝以减少过拟合
• 正则化以防止过拟合

这些特点使得 XGBoost 成为解决许多机器学习问题的流行且强大的工具。

第19.1步：XGBoost超参数调优

XGBoost (eXtreme Gradient Boosting)

XGBoost (eXtreme Gradient Boosting) 是一个用于梯度提升的开源库，广泛用于分类和回归问题。它代表了极端梯度提升，是一种针对速度和性能进行优化的梯度提升树的实现。XGBoost 是一个高度灵活的算法，允许用户定义自定义的目标和评估标准，并有效地处理缺失值。

XGBoost 优势：

• 正则化： 与标准的 GBM 实现不同，XGBoost 具有正则化功能，有助于减少过拟合。

• 快速并行处理： XGBoost 实现了并行处理，使其比 GBM 快得多。它还支持 Hadoop 实现。

• 高度灵活： XGBoost 允许用户定义自定义的优化目标和评估标准，提供了一种新的定制级别。

• 处理缺失值： XGBoost 内置了处理缺失值的例程，并且可以学习如何处理未来的预测中的缺失值。

• 有效的树修剪： XGBoost 进行分割直到达到指定的最大深度，然后修剪树，而 GBM 在遇到负损失时停止分割。

• 内置的交叉验证和持续训练： XGBoost 允许在每次提升迭代过程中进行交叉验证，从而更容易确定最佳迭代次数。此外，它可以从上一次运行的最后一次迭代开始训练。

第19.1步：XGBoost超参数调优

使用XGBoost构建模型很容易，但是改进模型需要超参数调优。这涉及到调整特定的设置以优化模型的性能。确定正确的超参数集合及其理想值是具有挑战性的，需要仔细的实验和分析。尽管在微调超参数方面存在困难，但XGBoost仍然是预测建模的高效解决方案。

XGBoost中最常用的超参数:

• eta (学习率): 用于更新中的步长缩减，以防止过拟合。

• max_depth: 基学习器的最大树深度。增加此值将使模型更复杂，更容易过拟合。

• gamma: 在树的叶节点上进行进一步分区所需的最小损失减少量。

• lambda (reg_lambda): 权重的L2正则化项。增加此值将使模型更保守。

• alpha (reg_alpha): 权重的L1正则化项。增加此值将强制进行更多的特征选择。

• subsample: 训练实例的子样本比例。将其设置为小于1的值将使模型更随机。

• colsample_bytree: 构建每棵树时的列子样本比例。

• colsample_bylevel: 每个级别的列子样本比例。

• n_estimators: 森林中的树的数量。

• max_leaf_nodes: 树中的最大终端节点或叶节点数。

• max_delta_step: 每个叶节点的最大增量步长。它用于进一步控制每个实例的权重值范围。

• scale_pos_weight: 负类别数与正类别数的比例，控制正负权重的平衡，对于不平衡的类别很有用。

• min_child_weight: 子节点中所需的最小实例权重（海森）。如果树分区步骤导致叶节点的实例权重之和小于min_child_weight，则构建过程将放弃进一步分区。

• booster: XGBoost使用的底层模型，可以是基于树的（gbtree）或线性的（gblinear）。基于树的增强模型始终优于线性增强模型，因此后者很少使用。

• Objective: 定义用于评估模型性能的损失函数。

• eval_metric: 指定用于在训练和测试过程中评估模型性能的度量标准。

我们可以再次设置每个超参数的取值范围，以便我们考虑XGBoost分类器的最佳组合超参数，然后使用tune_clf_hyperparameters函数来找到提供最佳结果的超参数组合。

# 使用train_test_split函数对数据进行训练集和测试集的划分
# 参数X为特征数据，y为目标数据
# test_size表示测试集所占的比例，这里设置为0.2，即测试集占总数据的20%
# random_state表示随机种子，用于保证每次划分的结果一致，这里设置为0
# stratify表示按照目标数据y的分布进行划分，保证训练集和测试集中各类别样本的比例相同
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)

定义超参数网格：

# 定义不平衡比例
ratio = sum(y_train==0)/sum(y_train==1) 

# 定义超参数网格搜索的参数范围
xgb_param_grid = {
    'max_depth': [5, 6, 7],  # 决策树的最大深度
    'learning_rate': [0.1, 0.2, 0.3],  # 学习率
    'n_estimators': [50, 100, 200],  # 弱学习器的数量
    'min_child_weight': [1, 5, 10],  # 决定叶子节点的最小权重和
    'scale_pos_weight': [ratio, ratio*1.3, ratio*1.5],  # 正负样本的权重比例
    'subsample': [0.6, 0.8, 1.0],  # 每棵树随机采样的比例
    'colsample_bytree': [0.6, 0.8, 1.0],  # 每棵树在特征维度上的随机采样比例
    'colsample_bylevel': [0.6, 0.8, 1.0],  # 每个级别的树在特征维度上的随机采样比例
    'reg_alpha': [0, 0.1, 1],  # L1正则化项的权重
    'reg_lambda': [0, 0.1, 1],  # L2正则化项的权重
    'max_delta_step': [0, 1, 2],  # 每棵树权重估计的最大步长
    'gamma': [0, 0.1, 1],  # 控制树的叶子节点分裂的最小损失减少量
    'max_leaf_nodes': [2, 4, 6]  # 每棵树的最大叶子节点数量
}

由于XGBoost超参数的数量很大，设置超参数的过程将非常耗时。因此，我们将网格值集合缩小，并最终得到了我们XGBoost分类器的以下超参数组合：

# 导入XGBoost分类器模块
from xgboost import XGBClassifier

# 初始化XGBoost分类器
xgb_opt = XGBClassifier(max_depth=5,  # 决策树的最大深度
                        learning_rate=0.3,  # 学习率
                        n_estimators=200,  # 弱分类器的个数
                        min_child_weight=1,  # 决定最小叶子节点样本权重和
                        scale_pos_weight=1.5,  # 正样本权重的比例
                        colsample_bytree=0.8,  # 每棵树的特征采样比例
                        gamma=0.1,  # 控制树的叶子节点分裂的最小损失减少量
                        booster='gbtree',  # 使用gbtree作为基分类器
                        objective='binary:logistic',  # 二分类问题，使用逻辑回归作为目标函数
                        eval_metric='error',  # 评估指标为错误率
                        random_state=0)  # 随机种子，保证结果的可重复性

# 训练XGBoost分类器
xgb_opt.fit(X_train, y_train)

XGBClassifier(base_score=0.5, booster='gbtree', callbacks=None,
              colsample_bylevel=1, colsample_bynode=1, colsample_bytree=0.8,
              early_stopping_rounds=None, enable_categorical=False,
              eval_metric='error', gamma=0.1, gpu_id=-1,
              grow_policy='depthwise', importance_type=None,
              interaction_constraints='', learning_rate=0.3, max_bin=256,
              max_cat_to_onehot=4, max_delta_step=0, max_depth=5, max_leaves=0,
              min_child_weight=1, missing=nan, monotone_constraints='()',
              n_estimators=200, n_jobs=0, num_parallel_tree=1, predictor='auto',
              random_state=0, reg_alpha=0, reg_lambda=1, ...)

确定XGBoost中最佳的超参数集是非常耗时的，所以我们没有深入研究！

第19.2步：XGBoost特征子集选择

特征子集选择对于XGBoost分类器同样重要。特征子集选择有助于降低模型的复杂性，减少过拟合，并提高模型的准确性。通过选择最相关的特征，XGBoost可以专注于最重要的信息，并进行更准确的预测：

drop_column_importance_plot(xgb_opt, X_train, y_train)

特征重要性分析的结果显示，数据集中的一些特征对于准确预测目标变量起到了负面作用。因此，我们从数据集中移除了这些特征：

# 调用函数：计算特征重要性
feature_importances = drop_column_importance(xgb_opt, X_train, y_train, 0.002)

# 根据特征重要性筛选数据集
selected_features = feature_importances[feature_importances['feature importance'] > 0.002]['feature']
X_train = X_train[selected_features]
X_test = X_test[selected_features]

让我们在删除无关特征后再次训练我们的模型：

# 导入XGBoost分类器模块
from xgboost import XGBClassifier

# 初始化XGBoost分类器
xgb = XGBClassifier(max_depth=5,  # 决策树的最大深度
                    learning_rate=0.3,  # 学习率
                    n_estimators=200,  # 决策树的数量
                    min_child_weight=1,  # 决策树叶子节点的最小权重
                    scale_pos_weight=1.5,  # 正样本权重的比例
                    colsample_bytree=0.8,  # 每棵决策树使用的特征比例
                    gamma=0.1,  # 控制决策树的叶子节点分裂的最小损失减少量
                    booster='gbtree',  # 使用的基础模型类型
                    objective='binary:logistic',  # 目标函数类型
                    eval_metric='error',  # 评估指标类型
                    random_state=0)  # 随机种子

# 训练XGBoost分类器
xgb.fit(X_train, y_train)

XGBClassifier(base_score=0.5, booster='gbtree', callbacks=None,
              colsample_bylevel=1, colsample_bynode=1, colsample_bytree=0.8,
              early_stopping_rounds=None, enable_categorical=False,
              eval_metric='error', gamma=0.1, gpu_id=-1,
              grow_policy='depthwise', importance_type=None,
              interaction_constraints='', learning_rate=0.3, max_bin=256,
              max_cat_to_onehot=4, max_delta_step=0, max_depth=5, max_leaves=0,
              min_child_weight=1, missing=nan, monotone_constraints='()',
              n_estimators=200, n_jobs=0, num_parallel_tree=1, predictor='auto',
              random_state=0, reg_alpha=0, reg_lambda=1, ...)

第19.3步：XGBoost模型评估

让我们使用model_evaluation函数评估我们最终的XGBoost分类器的性能：

model_evaluation(xgb, X_train, X_test, y_train, y_test, 'Primary XGBoost')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       1.00      1.00      1.00      3569
           1       1.00      1.00      1.00       346

    accuracy                           1.00      3915
   macro avg       1.00      1.00      1.00      3915
weighted avg       1.00      1.00      1.00      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       0.99      1.00      1.00       892
           1       0.98      0.93      0.95        87

    accuracy                           0.99       979
   macro avg       0.98      0.96      0.97       979
weighted avg       0.99      0.99      0.99       979

XGBoost分类器在少数类上有相当严重的过拟合问题，需要调整超参数以减少方差并防止过拟合。

如何减少我们的XGBoost分类器的方差？

• min_child_weight: 我们可以增加min_child_weight的值来控制树模型的复杂度，防止过拟合。

• max_depth: 我们可以减小max_depth的值，防止模型从训练数据中学习过多，减少模型的方差。

• gamma: 我们可以增加gamma的值来控制进行分裂所需的最小损失减少量，以减少模型的方差。

• lambda: 我们可以增加lambda的值来添加正则化，控制过拟合。

• subsample: 我们可以减小subsample的值，减少用于拟合每棵树的样本数量，减少模型的方差。

• colsample_bytree: 我们可以减小colsample_bytree的值，减少每棵树中使用的特征数量，避免过拟合。

• n_estimators: 我们可以增加树的数量来减少模型的方差。

在获得的超参数的最优值中，我们只将max_depth的值从5降低到4，以部分避免过拟合。

# 导入XGBoost分类器
from xgboost import XGBClassifier

# 初始化XGBoost分类器
xgb_final = XGBClassifier(max_depth=4,  # 决策树的最大深度
                          learning_rate=0.3,  # 学习率
                          n_estimators=200,  # 决策树的个数
                          min_child_weight=1,  # 决策树叶子节点的最小权重
                          scale_pos_weight=1.5,  # 正样本的权重
                          colsample_bytree=0.8,  # 每棵决策树使用的特征比例
                          gamma=0.1,  # 控制决策树的叶子节点分裂的程度
                          booster='gbtree',  # 使用的弱学习器类型
                          objective='binary:logistic',  # 目标函数
                          eval_metric='error',  # 评估指标
                          random_state=0)  # 随机种子

# 训练XGBoost分类器
xgb_final.fit(X_train, y_train)

XGBClassifier(base_score=0.5, booster='gbtree', callbacks=None,
              colsample_bylevel=1, colsample_bynode=1, colsample_bytree=0.8,
              early_stopping_rounds=None, enable_categorical=False,
              eval_metric='error', gamma=0.1, gpu_id=-1,
              grow_policy='depthwise', importance_type=None,
              interaction_constraints='', learning_rate=0.3, max_bin=256,
              max_cat_to_onehot=4, max_delta_step=0, max_depth=4, max_leaves=0,
              min_child_weight=1, missing=nan, monotone_constraints='()',
              n_estimators=200, n_jobs=0, num_parallel_tree=1, predictor='auto',
              random_state=0, reg_alpha=0, reg_lambda=1, ...)

让我们评估我们的最终XGBoost分类器：

model_evaluation(xgb_final, X_train, X_test, y_train, y_test, 'XGBoost')

	  Classification report for training set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       1.00      1.00      1.00      3569
           1       1.00      1.00      1.00       346

    accuracy                           1.00      3915
   macro avg       1.00      1.00      1.00      3915
weighted avg       1.00      1.00      1.00      3915


	   Classification report for test set
-------------------------------------------------------
              precision    recall  f1-score   support

           0       1.00      1.00      1.00       892
           1       0.99      0.95      0.97        87

    accuracy                           0.99       979
   macro avg       0.99      0.98      0.98       979
weighted avg       0.99      0.99      0.99       979

XGBoost分类器是我们处理不平衡数据集的终极武器。正如可以看到的，我们的XGBoost分类器在f1-score上达到了惊人的97%，在AUC上达到了99.87%，这是所有经过审查的分类器中表现最好的。在979名银行客户中，该模型仅在5个案例中出现错误，以预测客户是否接受贷款。

xgb_result = metrics_calculator(xgb_final, X_test, y_test, 'XGBoost')

第20步：结论

如前所述，对于这个项目来说，最重要的指标是类别为’1’的f1-score。高的f1-score表示在尽可能识别出尽可能多的潜在贷款客户（高召回率）的同时，最小化误报的数量（高精确率），这对于银行来说至关重要，可以提高存款人转变为借款人的转化率，同时降低营销活动的成本。

接下来，我们可以根据指标检查所有先前分类器的性能：

# 将之前分类器的性能结果连接成一个单独的数据框
results = pd.concat([cnb_result, bnb_result, logreg_result, knn_result, svm_result, dt_result,
           rf_result, et_result, ada_result, gbc_result, xgb_result], axis=1).T

# 根据F1-score值降序对数据框进行排序
results.sort_values(by='F1-score', ascending=False, inplace=True)

# 对F1-score列进行着色
results.style.applymap(lambda x: 'background-color: royalblue', subset='F1-score')

	Accuracy	Precision	Recall	F1-score	AUC
XGBoost	99.49%	98.81%	95.4%	97.08%	99.87%
Extra Trees	99.18%	98.77%	91.95%	95.24%	99.84%
Gradient Boosting	99.18%	98.77%	91.95%	95.24%	99.92%
AdaBoost	98.98%	96.39%	91.95%	94.12%	99.5%
Random Forest	98.98%	98.73%	89.66%	93.98%	99.81%
SVM	98.47%	93.9%	88.51%	91.12%	98.36%
K-Nearest Neighbors	98.47%	95.0%	87.36%	91.02%	97.0%
Decision Tree	98.47%	96.15%	86.21%	90.91%	97.48%
Logistic Regression	94.79%	72.5%	66.67%	69.46%	95.96%
Bernoulli Naive Bayes	93.87%	72.13%	50.57%	59.46%	94.51%
Complement Naive Bayes	86.01%	38.32%	94.25%	54.49%	93.27%

在下面，我们可以看到以条形图形式显示的所有先前分类器中类别’1’的f1-score：

# 准备数值

# 按照'F1-score'列的值进行升序排序
results.sort_values(by='F1-score', ascending=True, inplace=True)

# 将'F1-score'列的百分号去除，并将其转换为浮点数
f1_scores = results['F1-score'].str.strip('%').astype(float)

# 绘制条形图

# 创建一个大小为(10, 8)、分辨率为70的图表
fig, ax = plt.subplots(figsize=(10, 8), dpi=70)

# 绘制水平条形图，x轴为f1_scores，y轴为results的索引，颜色为'royalblue'
ax.barh(results.index, f1_scores, color='royalblue')

# 注释数值和索引

# 遍历f1_scores和results的索引
for i, (value, name) in enumerate(zip(f1_scores, results.index)):
    # 在图表上方的位置添加注释，注释内容为value的值加上0.5，注释的y坐标为i，注释的水平对齐方式为'left'，垂直对齐方式为'center'，字体加粗，颜色为'midnightblue'
    ax.text(value+0.5, i, f"{value}%", ha='left', va='center', fontweight='bold', color='midnightblue')
    # 在坐标(10, i)的位置添加注释，注释内容为name，注释的水平对齐方式为'left'，垂直对齐方式为'center'，字体加粗，颜色为'white'，字体大小为18
    ax.text(10, i, name, ha='left', va='center', fontweight='bold', color='white', fontsize=18)

# 移除y轴刻度
ax.set_yticks([])

# 设置x轴的范围为0到110
ax.set_xlim([0,110])

# 添加标题和x轴标签
plt.title("F1-score for class '1'", fontweight='bold', fontsize=22)
plt.xlabel('Percentages (%)', fontsize=16)

# 显示图表
plt.show()

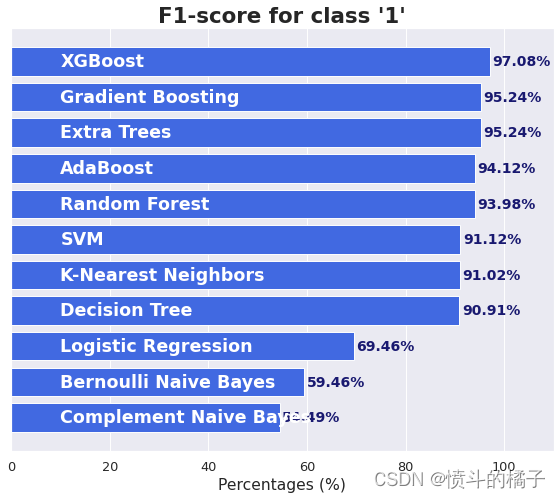
🏆 在所有测试的分类器中，“XGBoost分类器”在识别潜在贷款客户方面表现最好：

• 准确率 = 99.49%
• F1分数 = 97.08%
• 精确率 = 98.81%
• 召回率 = 95.4%
• AUC = 99.87%

🏆 根据以前的特征重要性图，Education（教育程度）、Income（收入）、Family（家庭）、CCAvg（平均信用卡支出）和CD Account（存款账户）在识别潜在贷款客户中起着最重要的作用。**