Scikit-Learn 1.4使用指南：有监督学习概率校准 Probability Calibration-CSDN博客

本文链接：https://blog.csdn.net/wjjc1017/article/details/136035634

文章目录

sklearn.calibration

在进行分类时，通常不仅要预测类别标签，还要获得相应标签的概率。这个概率给出了预测的一种置信度。有些模型可能给出了较差的类别概率估计，甚至有些模型不支持概率预测（例如，~sklearn.linear_model.SGDClassifier 的某些实例）。校准模块允许您更好地校准给定模型的概率，或者为模型添加概率预测的支持。

经过良好校准的分类器是指其predict_proba方法的输出可以直接解释为置信水平的概率分类器。例如，一个良好校准的（二元）分类器应该对样本进行分类，使得在给定一个接近0.8的predict_proba值的样本中，大约80%实际上属于正类。

在展示如何重新校准分类器之前，我们首先需要一种方法来检测分类器的校准程度。

[!NOTE]
严格的适用于概率预测的得分规则，如sklearn.metrics.brier_score_loss和sklearn.metrics.log_loss，同时评估模型的校准性（可靠性）和区分能力（分辨率），以及数据的随机性（不确定性）。这是根据Murphy的著名Brier得分分解得出的。由于不清楚哪个术语占主导地位，该得分在仅用于评估校准时的用途有限（除非计算分解的每个术语）。较低的Brier损失并不一定意味着更好的校准模型，它也可能意味着校准更差的模型，但具有更强的区分能力，例如使用更多的特征。

校准曲线

校准曲线，也称为可靠性图（Wilks 1995），比较了二元分类器的概率预测的校准程度。它将正类别的频率（更准确地说，是条件事件概率 $KaTeX parse error: Expected 'EOF', got '_' at position 20: …1|\text{predict_̲proba})$ 的估计）绘制在y轴上，将模型的预测概率predict_proba绘制在x轴上。关键部分是获取y轴的值。在scikit-learn中，通过将预测进行分组，使得x轴表示每个分组中的平均预测概率。然后，y轴是给定该分组预测的正类别的正例比例，即每个分组中属于正类别的样本的比例。

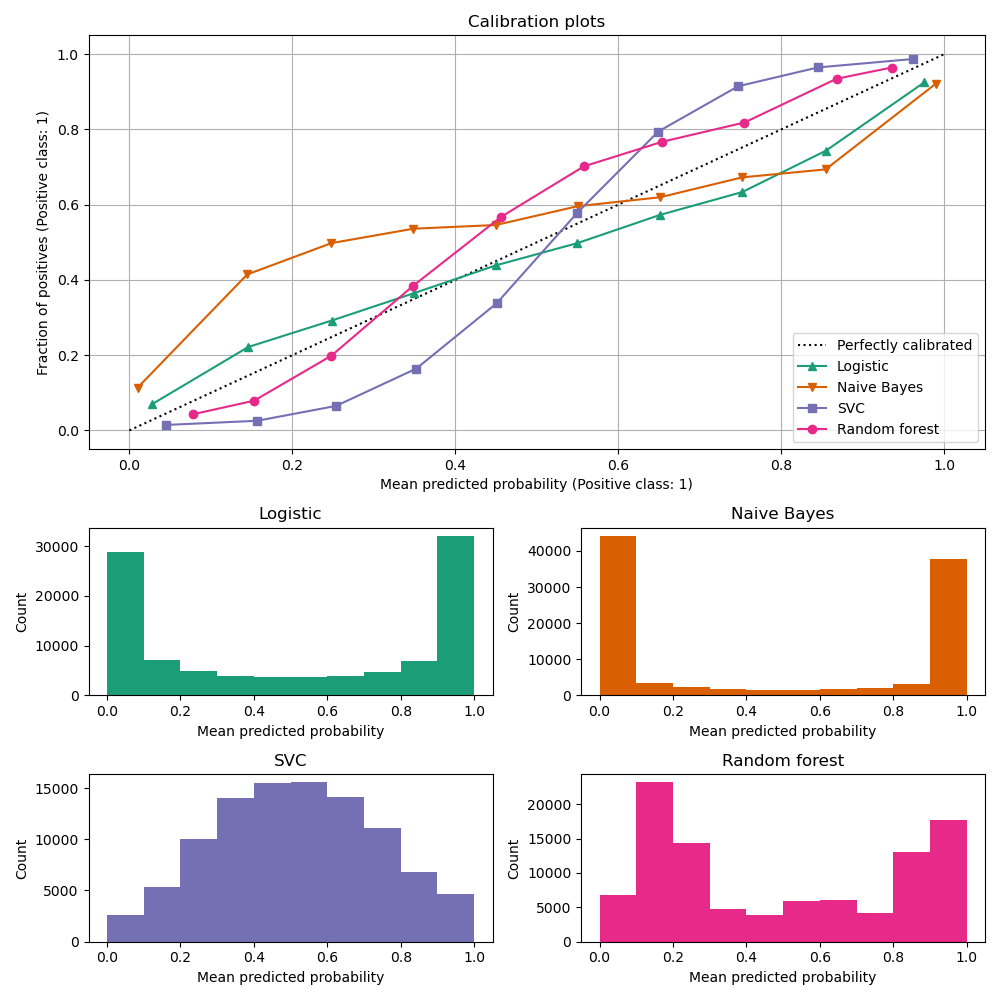
顶部的校准曲线图是使用CalibrationDisplay.from_estimator创建的，它使用calibration_curve计算每个分组的平均预测概率和正例比例。CalibrationDisplay.from_estimator接受一个已拟合的分类器作为输入，用于计算预测概率。因此，分类器必须具有predict_proba方法。对于那些没有predict_proba方法的少数分类器，可以使用CalibratedClassifierCV来校准分类器输出为概率。

底部的直方图通过显示每个预测概率分组中的样本数量，提供了对每个分类器行为的一些见解。

sklearn.linear_model

LogisticRegression默认情况下返回经过良好校准的预测，因为它的损失函数具有其损失的典型链接函数，即log_loss的logit链接。这导致了所谓的平衡特性，参见Logistic_regression。相比之下，其他显示的模型返回有偏的概率，每个模型的偏差不同。

sklearn.naive_bayes

GaussianNB（朴素贝叶斯）倾向于将概率推向0或1（请注意直方图中的计数）。这主要是因为它假设在给定类别的情况下，特征是条件独立的，而在这个数据集中包含了2个冗余特征，这个假设并不成立。

sklearn.ensemble

RandomForestClassifier显示了相反的行为：直方图显示了概率大约为0.2和0.9的峰值，而接近0或1的概率非常罕见。Niculescu-Mizil和Caruana给出了一个解释：“诸如bagging和随机森林之类的方法，这些方法从一组基本模型的预测中平均预测，可能在接近0和1的预测上出现困难，因为基本模型的方差会使应该接近零或一的预测偏离这些值。因为预测被限制在区间[0,1]内，由方差引起的错误往往在接近零和一的地方是单向的。例如，如果一个模型应该对一个案例预测p = 0，那么bagging能够实现这一点的唯一方法是如果所有袋装树都预测为零。如果我们向袋装模型添加噪声，这个噪声将导致一些树对这个案例预测大于0的值，从而使袋装集合的平均预测远离0。我们在随机森林中最明显地观察到这种效应，因为随机森林训练的基本层级树由于特征子集而具有相对较高的方差。”因此，校准曲线显示了一个特征的S形状，表明分类器可以更加相信自己的“直觉”，通常返回更接近0或1的概率。

sklearn.svm

LinearSVC（SVC）显示了比随机森林更加S形状的曲线，这是最大间隔方法的典型特征（与Niculescu-Mizil和Caruana进行比较），这些方法侧重于接近决策边界（支持向量）的难以分类的样本。

校准分类器

sklearn.calibration

校准分类器包括拟合一个回归器（称为校准器），将分类器的输出（由decision_function或predict_proba给出）映射到[0, 1]范围内的校准概率。将给定样本的分类器输出表示为 $f_i$ ，校准器试图预测条件事件概率 $P(y_i = 1 | f_i)$ 。

理想情况下，校准器应该在与首次拟合分类器的训练数据独立的数据集上进行拟合。这是因为分类器在其训练数据上的性能会优于新数据。使用训练数据的分类器输出来拟合校准器将导致一个有偏的校准器，它将映射到比实际更接近0和1的概率。

用法

使用CalibratedClassifierCV类来校准分类器。

CalibratedClassifierCV使用交叉验证方法来确保始终使用无偏数据来拟合校准器。数据被分成k个（训练集，测试集）对（由cv确定）。当ensemble=True（默认值）时，以下过程对每个交叉验证拆分独立重复：首先在训练子集上训练base_estimator的克隆。然后使用其在测试子集上的预测来拟合校准器（sigmoid或isotonic回归器）。这将导致k个（分类器，校准器）对的集合，其中每个校准器将其对应分类器的输出映射到[0, 1]范围内。每个对都在calibrated_classifiers_属性中公开，其中每个条目都是具有predict_proba方法的校准分类器，输出校准概率。主CalibratedClassifierCV实例的predict_proba输出对应于calibrated_classifiers_列表中k个估计器的预测概率的平均值。predict的输出是具有最高概率的类别。
ensemble=True 的主要优势在于从传统的集成效应（类似于“bagging”）中获益。得到的集成模型既应该具有良好的校准性，又应该比 ensemble=False 时稍微更准确一些。而使用 ensemble=False 的主要优势在于计算上的便利性：它通过仅训练单个基分类器和校准器对来减少整体拟合时间，减小最终模型的大小并增加预测速度。

另外，可以通过设置 cv=“prefit” 来校准已经拟合好的分类器。在这种情况下，数据不会被分割，而是全部用于拟合回归器。用户需要确保用于拟合分类器的数据与用于拟合回归器的数据不重叠。

CalibratedClassifierCV 支持通过 method 参数使用两种回归技术进行校准：“sigmoid” 和 “isotonic”。

Sigmoid

Sigmoid 回归器，即 method=“sigmoid”，基于 Platt 的逻辑模型：

$p(y_i = 1 | f_i) = \frac{1}{1 + \exp(A f_i + B)} \,,$

其中 $y_i$ 是样本 $i$ 的真实标签， $f_i$ 是样本 $i$ 的未校准分类器的输出。 $A$ 和 $B$ 是在拟合回归器时确定的实数。

Sigmoid 方法假设可以通过将 sigmoid 函数应用于原始预测来修正校准曲线。在 Platt 1999 年的第 2.1 节中，通过在各种基准数据集上对带有常见核函数的 svm 进行实证验证，证明了这种假设的合理性。但是，这种假设不一定适用于所有情况。此外，逻辑模型在校准误差对称时效果最好，即每个二元类别的分类器输出服从相同方差的正态分布。这可能会成为高度不平衡分类问题的问题，其中输出的方差不相等。

总的来说，这种方法在样本量较小或未校准模型置信度不足且高输出和低输出的校准误差相似时效果最好。

Isotonic

method=“isotonic” 使用非参数的保序回归器，输出一个阶梯非递减函数，参见 sklearn.isotonic。它最小化以下目标函数：

$\sum_{i=1}^{n} (y_i - \hat{f}_i)^2$

满足当 $f_i \geq f_j$ 时， $\hat{f}_i \geq \hat{f}_j$ 。 $y_i$ 是样本 $i$ 的真实标签， $\hat{f}_i$ 是校准分类器对样本 $i$ 的输出（即校准概率）。与 “sigmoid” 相比，这种方法更加通用，因为它的唯一限制是映射函数单调递增。因此，它更强大，可以纠正未校准模型的任何单调失真。然而，它更容易过拟合，特别是在小型数据集上。

总的来说，当有足够的数据（大约大于1000个样本）以避免过拟合时，“isotonic” 的性能将与 “sigmoid” 相当或更好。

[!NOTE]
对 AUC 等排名指标的影响

通常预期校准不会影响诸如 ROC-AUC 等排名指标。然而，当使用 method=“isotonic” 进行校准时，这些指标可能在校准后有所不同，因为保序回归会在预测概率中引入并列。这可以视为模型预测的不确定性范围。如果您严格要求保持排名和 AUC 分数，请使用 method=“sigmoid”，因为它是一个严格单调的转换，因此保持排名不变。

多类支持

无论是 isotonic 还是 sigmoid 回归器，都仅支持 1 维数据（例如二元分类输出），但如果基分类器支持多类预测，则可以扩展为多类分类。对于多类预测，CalibratedClassifierCV 以 ovr_classification 的方式为每个类别分别进行校准。在预测概率时，会分别预测每个类别的校准概率。由于这些概率不一定总和为一，因此会进行后处理以对其进行归一化。

示例：

sphx_glr_auto_examples_calibration_plot_calibration_curve.py
sphx_glr_auto_examples_calibration_plot_calibration_multiclass.py
sphx_glr_auto_examples_calibration_plot_calibration.py
sphx_glr_auto_examples_calibration_plot_compare_calibration.py

参考文献：

[1]

Allan H. Murphy (1973). “A New Vector Partition of the Probability Score” Journal of Applied Meteorology and Climatology

[2]

On the combination of forecast probabilities for consecutive precipitation periods.Wea. Forecasting, 5, 640–650., Wilks, D. S., 1990a

[3] (1,2,3)

Predicting Good Probabilities with Supervised Learning, A. Niculescu-Mizil & R. Caruana, ICML 2005

[4] (1,2)

Probabilistic Outputs for Support Vector Machines and Comparisons to Regularized Likelihood Methods. J. Platt, (1999)

[5]

Transforming Classifier Scores into Accurate Multiclass Probability Estimates. B. Zadrozny & C. Elkan, (KDD 2002)

[6]

Predicting accurate probabilities with a ranking loss. Menon AK, Jiang XJ, Vembu S, Elkan C, Ohno-Machado L. Proc Int Conf Mach Learn. 2012;2012:703-710

[7]

Beyond sigmoids: How to obtain well-calibrated probabilities from binary classifiers with beta calibration Kull, M., Silva Filho, T. M., & Flach, P. (2017).

[8]

Mario V. Wüthrich, Michael Merz (2023). “Statistical Foundations of Actuarial Learning and its Applications” Springer Actuarial