深入探讨深度学习

深入探讨深度学习

深度学习已成为现代人工智能的基础支柱，推动了计算机视觉和自然语言处理（NLP）等多个领域的发展。继我之前关于大型语言模型训练流程的文章之后，我将探讨深度学习中的基本概念和技术，包括神经网络的基本构件、卷积神经网络架构、基本矩阵操作、量化技术和优化器。我将引用对深度学习领域产生重大影响的研究论文。

深度学习简介

深度学习，机器学习的一个子集以及生成型AI的基础，图像1.，利用具有多层的神经网络对数据中的复杂模式进行建模。这些模型在各种领域取得了最先进的成果，从图像分类到语音识别，并在生成型AI技术的发展中发挥了重要作用。

2006年，Geoffrey Hinton及其同事的研究标志着深度学习的重大突破，他们在论文“深度信念网络的快速学习算法”中引入了深度信念网络（DBNs）的概念。[[1]](https://www.cs.toronto.edu/~hinton/absps/ncfast.pdf) 这项工作为训练深度神经网络奠定了基础，采用逐层无监督预训练后跟随有监督的微调。这种方法有效地解决了如梯度消失等挑战，这些挑战在此之前一直阻碍着深度网络的训练。这种开创性的方法，以及卷积神经网络（CNN）等技术的进步，成为深度学习成功的核心，使其成为现代人工智能中一项强大的工具。

Image 1. 深度学习是机器学习的一个子集

深度学习中的正则化和归一化技术

正则化和归一化技术在增强深度学习模型的性能和鲁棒性方面是基础，特别是在防止过拟合和提高泛化能力方面。这些方法在各种架构中至关重要，包括自编码器，自编码器旨在学习有效的数据表示，用于降维、特征学习和数据去噪等任务。

自编码器由编码器和解码器组成，编码器将输入数据压缩到潜在空间，解码器则重建输入，得益于诸如**dropout（丢弃法）和batch normalization（批标准化）**等技术。丢弃法是由Srivastava等人于2014年提出的一种广泛使用的正则化方法，通过在训练过程中随机丢弃单元及其连接来帮助防止过拟合。这促使网络发展冗余表示，确保模型不对任何单一特征过度依赖。在自编码器的上下文中，丢弃法在编码器和解码器层中尤为有效，帮助在不同数据输入下保持学习表示的完整性。

批量归一化，由 Ioffe 和 Szegedy 于 2015 年提出 [[3]](https://arxiv.org/abs/1502.03167)，是另一种关键技术，它对每层的输入进行归一化，跨越小批量。这个过程通过减轻内部协变量转移，稳定和加速训练，内部协变量转移是指每层输入的分布在训练过程中发生变化的情况。在更深的网络中，包括自编码器，批量归一化有助于保持一致的激活尺度，从而导致更快的收敛和更好的性能。然而，当批量大小足够大以提供可靠的均值和方差估计时，它的效果最好。

分组卷积，由Xception和MobileNet等架构所推广，进一步推动了深度学习模型的优化。通过将输入通道划分为多个组，每个组由自己的一组滤波器处理，分组卷积在降低计算复杂性的同时保持性能。这种方法在资源受限的环境中尤其有利，在这些环境中，高效的模型部署至关重要。AlexNet架构由Krizhevsky等人在2012年提出[[4]](https://papers.nips.cc/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf)，是第一批利用分组卷积的架构之一，展示了在不牺牲准确性的前提下优化模型架构的有效性。

另一方面，实例归一化，由Ulyanov、Vedaldi和Lempitsky于2016年提出 [[5]](https://arxiv.org/abs/1607.08022)，单独对每个实例进行归一化。这种技术在风格迁移和生成建模等任务中特别有利，其中保持独特的实例特征至关重要。与批量归一化不同，实例归一化允许模型专注于单个输入特征，而不受更广泛的微型批量统计的影响，因此在需要保持个体风格或细粒度细节的场景中更受欢迎。

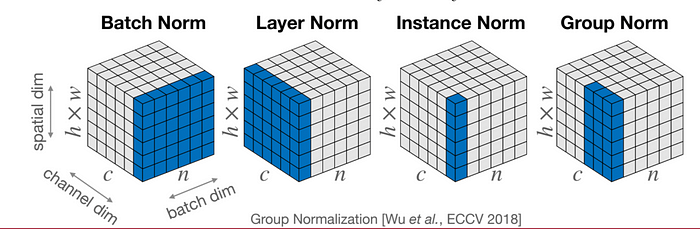
Image 2. 不同类型的归一化

结合 dropout、批量归一化和实例归一化，这些技术对深度学习架构的成功至关重要。这些技术不仅有助于防止过拟合，还使模型能够在广泛的任务中学习稳定且具有可推广性的特征。随着深度学习领域的不断发展，这些正则化和归一化方法的战略应用将在推动神经网络在图像处理到自然语言理解等不同领域的能力方面发挥关键作用。

此外，还有其他类型的归一化技术，例如层归一化和组归一化，这些在图2中与批量归一化和实例归一化一起进行了可视化。这些技术通过在不同维度上归一化数据，为稳定神经网络的训练提供了替代方法，从而有助于各种深度学习模型的鲁棒性和有效性。

神经网络架构

神经网络是由基本组件构建而成的，如卷积层、全连接层和递归层，每个组件在处理数据时都发挥着独特的作用。卷积层在卷积神经网络（CNN）等架构中起着关键作用，通过使用共享权重（卷积核）来检测边缘和纹理等特征，在图像识别和物体检测方面表现出色。LeNet-5架构，由LeCun等人（1998年）引入，是展示卷积层强大功能的里程碑。

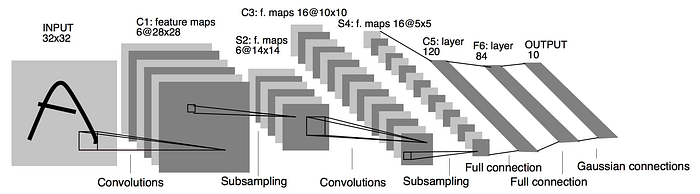
Image 3. LeNet-5 架构

全连接层则将一层中的每个神经元与下一层的每个神经元连接，提供了灵活性，但通常会导致大量参数和更高的过拟合风险。在2015年，He等人提出的ResNet标志着一个重要的进展，通过引入残差连接解决了深度网络中的梯度消失问题，使梯度能够更容易地在网络中传播。

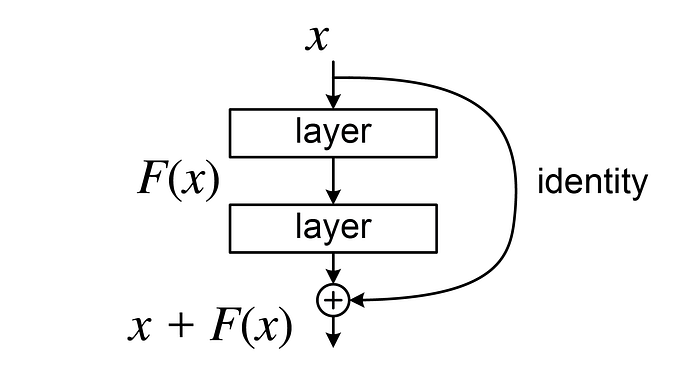
Image 4. 深度残差网络中的残差块

循环结构，特别是循环神经网络（RNN）及其变种长短时记忆（LSTM）网络，图 5，由Hochreiter和Schmidhuber于1997年提出 [[8]](https://deeplearning.cs.cmu.edu/F23/document/readings/LSTM.pdf)，在处理涉及顺序数据的任务中至关重要，如自然语言处理和时间序列预测。这些层在时间步之间保持信息，使网络能够捕捉时间依赖性。

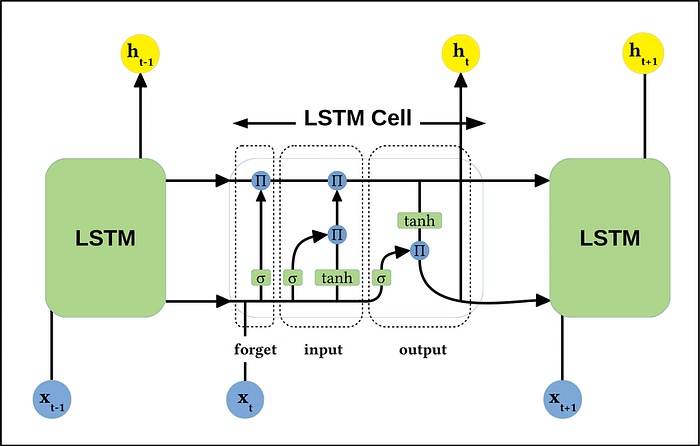
Image 5. 基本的长短期记忆（LSTM）架构。

最近，深度学习的焦点转向了注意力机制，这革命性地改变了该领域，使得模型能够动态地关注输入数据的不同部分。Transformer模型由Vaswani等人在2017年提出[[9]](https://arxiv.org/abs/1706.03762)， exemplifies这一转变，为像BERT和GPT这样的规模较大的模型铺平了道路，这些模型在从语言翻译到文本生成等任务中设定了新的基准。这一转变代表了神经网络发展的当前状态，注意力机制现在位于创新的前沿。

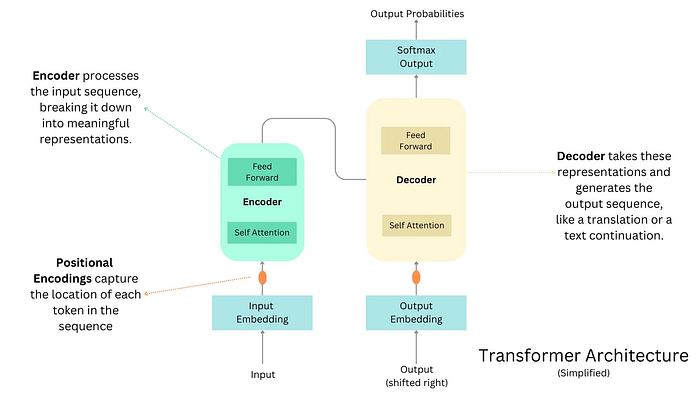
图像 6. Transformer 编码器-解码器架构

混合精度训练和量化技术的进展

混合精度训练，由Micikevicius等人在2018年推广 [[10]](https://arxiv.org/abs/1710.03740)，是一种通过结合16位（半精度）和32位（单精度）浮点运算来加速深度神经网络训练的技术。这种方法利用16位计算在大多数操作中的速度和内存效率，同时将32位精度保留用于对精度损失敏感的任务。这种平衡允许更快的训练和使用更大的模型。这种技术的一个关键组成部分是损失缩放，它通过将损失乘以一个大数来防止在反向传播过程中出现下溢，然后再缩放梯度。

现代的 GPU，如 NVIDIA 的 Volta、Ampere 和 Hopper 架构，针对混合精度训练进行了优化，采用了专门的 Tensor Cores。这些 Tensor Cores 是 NVIDIA 引入的，能够以 16 位精度执行乘法，同时以 32 位精度累积结果，图像 7，确保了速度和准确性。

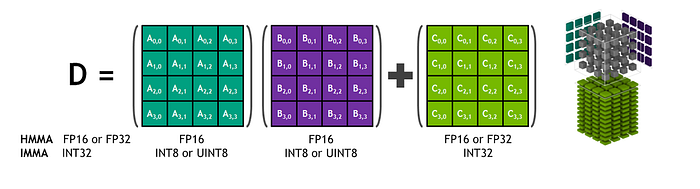
图片 7. Tensor Core 混合精度数学

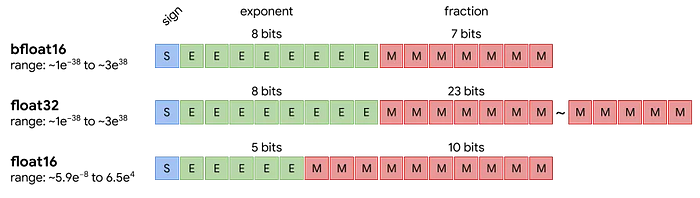
Image 8. 不同的浮点精度

基于Hopper架构，NVIDIA的Blackwell架构引入了针对混合精度和整数算术运算的进一步优化。Blackwell架构增强了混合精度能力，包括对8位和4位运算的改进支持，从而在不影响准确性的情况下加快了大规模AI模型的训练和推理。Blackwell中的Tensor Cores进一步优化，以更高效地处理更广泛的混合精度和整数算术运算，更好地与AI框架集成，并增强了对稀疏性的支持。这些改进导致了更快的计算时间和更低的内存使用。

量化感知训练 (QAT)，由 Jacob 等人 (2018) [[11]](https://arxiv.org/abs/1712.05877) 提出，是一种在训练过程中模拟量化与神经网络一起进行训练的技术。这种方法使模型能够适应量化引入的噪声，从而在将模型参数转换为更低精度（例如 8 位整数）时保持准确性。QAT 在将模型部署到优化为整数操作的硬件上时尤为有利，因为它不仅加速了计算，还由于整数运算的效率而降低了功耗。

然而，量化，特别是低位精度的量化，面临一个重要挑战，那就是激活值的量化。与权重不同，激活值的取值范围可以更广泛，这使得用更少的位数准确表示它们变得更加困难。这个问题在仅使用整数的算术中尤为重要，因为在范围和精度上的限制更加严格。Jacob 等人通过仔细校准激活值的范围并使用对称或非对称量化来解决这个挑战，从而减少误差，这对于在仅使用整数的推理中保持准确性至关重要。

提高训练效率

梯度检查点是一种通过以计算成本换取内存使用来提高训练效率的技术。该方法不是存储所有中间激活，而是在反向传播过程中重新计算部分激活，从而允许在不超过内存限制的情况下训练更大模型或批量大小。这种方法在陈等人2016年的出版物“以次线性内存成本训练深度网络”中得到了显著讨论 [[12]](https://arxiv.org/abs/1604.06174)。

剪枝通过消除不太重要的权重来减少模型大小，从而加速推理并减少内存使用。然而，这个过程通常会导致稀疏矩阵，这需要针对稀疏矩阵操作优化的专用GPU内核。没有这样的优化硬件支持，剪枝所带来的理论加速在实践中可能无法完全实现。Han等人（2015）的论文“深度压缩”[[13]](https://arxiv.org/pdf/1510.00149)提供了这些技术及其在优化深度学习模型以供部署方面影响的全面概述。例如，在边缘设备或计算资源有限的环境中，如果硬件有效地支持稀疏操作，剪枝可以非常有利。

深度学习中的自适应优化器

自适应优化器如 Adam (Kingma & Ba, 2014) [[14]](https://arxiv.org/pdf/1412.6980) 在深度学习中由于其动态学习率调整而成为标准。然而，标准的 Adam 有时会导致次优的泛化。为了解决这个问题，由 Loshchilov 和 Hutter (2019) 提出的 AdamW 在解耦权重衰减正则化中[[15]](https://arxiv.org/pdf/1711.05101) 将权重衰减与梯度更新解耦，从而提高了性能。AdamW 在训练过拟合问题较为严重的模型时特别有效，因为解耦的权重衰减提供了更好的正则化。

Prodigy，另一方面，是由Gilmer, Schoenholz和Riley（2020年）在Prodigy: Weight Averaging for Improved Generalization中提出的一种自适应优化器，该文献构建于这些思想之上，通过结合过去的梯度和当前的梯度趋势，更有效地调整学习率。这使得Prodigy特别适合在复杂或高度动态的环境中进行训练，在这些环境中，训练过程可能会经历数据分布或梯度行为的频繁变化。例如，Prodigy可能在处理非平稳数据的场景中优于AdamW，例如强化学习或在具有显著噪声或变异性的数据集上训练。相反，在更稳定的环境中，主要关注点是通过有效的正则化来避免过拟合，因此可能更倾向于使用AdamW。

参考文献

1. 深度信念网络 — Hinton, G. E., Osindero, S., & Teh, Y. W. (2006) — 深度信念网络的快速学习算法 — https://www.cs.toronto.edu/~hinton/absps/ncfast.pdf
2. 丢弃法 — Srivastava 等人 (2014) — 丢弃法：防止神经网络过拟合的一种简单方法 — https://jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf
3. 批量归一化 — Ioffe & Szegedy (2015) — 批量归一化：通过减少内部协变量偏移加速深度网络训练 — https://arxiv.org/abs/1502.03167
4. AlexNet — Krizhevsky et al. (2012) — 用深度卷积神经网络进行图像分类 — https://papers.nips.cc/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf
5. 实例归一化 — Ulyanov 等人 (2016) — 实例归一化：快速风格化的缺失成分 — https://arxiv.org/abs/1607.08022
6. LeNet-5 — LeCun 等人 (1998) — 基于梯度的学习应用于文档识别 —http://vision.stanford.edu/cs598_spring07/papers/Lecun98.pdf
7. ResNet — He et al. (2015) — 深度残差学习用于图像识别 — https://arxiv.org/abs/1512.03385
8. LSTM — Hochreiter 和 Schmidhuber (1997) — 长短期记忆 —https://deeplearning.cs.cmu.edu/F23/document/readings/LSTM.pdf
9. Transformer — Vaswani et al. (2017) — 注意力机制是你所需要的一切 — https://arxiv.org/abs/1706.03762
10. 混合精度训练 — Micikevicius et al. (2018) — https://arxiv.org/abs/1710.03740
11. 量化感知训练 (QAT) — Jacob et al. (2018) — https://arxiv.org/abs/2306.07215
12. 梯度检查点 — 陈等人 (2016) — 以亚线性内存成本训练深度网络 — https://arxiv.org/abs/1604.06174
13. 深度压缩 — Han et al. (2015) — 深度压缩：通过剪枝、训练量化和霍夫曼编码压缩深度神经网络 — https://arxiv.org/pdf/1510.00149.pdf
14. Adam — Kingma 和 Ba (2014) — Adam: 一种随机优化的方法 — https://arxiv.org/pdf/1412.6980.pdf.
15. AdamW — Loshchilov 和 Hutter (2019) — 解耦权重衰减正则化 — https://arxiv.org/pdf/1711.05101.pdf.
16. Prodigy — Gilmer, Schoenholz, 和 Riley (2020) — Prodigy: 权重平均以改善泛化能力 — https://arxiv.org/html/2306.06101v4.