V顶点数 E边数
建图
邻接矩阵
vector<vector<int>> GetMGraph(int numVertexes,int numEdges){
vector<vector<int>> graph(numVertexes,vector<int>(numVertexes,MAX));
int start,end,weight;
for(int i=0;i<numEdges;i++){
cin>>start>>end>>weight;
graph[start][end]=weight;
}
return graph;
}邻接表
vector<vector<int>> GetEGraph(int numEdges){
vector<vector<int>> Edges(numEdges,vector<int>(3,0));
int start,end,weight;
for(int i=0;i<numEdges;i++){
cin>>start>>end>>weight;
Edges[i][0]=start;
Edges[i][1]=end;
Edges[i][2]=weight;
}
return Edges;
}链式前向星
#define numv 1000
#define nume 100000
int head[numv]; //head[i]表示以i节点为出发节点的边的编号
int nextE[nume]; //nextE[i]表示和第i条边出发节点相同的一条边的编号
//i和nextE[i]为相同层级的边
int to[nume]; //to[i]表示第i条边指向的节点
int weight[nume]; //weight[i]表示第i条边的权值
int cnt=1;
void addedge(int u,int v,int w){
nextE[cnt]=head[u]; //将原来以u为起点的边并入cnt的同层级的边里
to[cnt]=v;
weight[cnt]=w;
head[u]=cnt++; //u为起点的边的编号
}
void getgraph(int n){
int u,v,w;
for(int i=0;i<n;i++){
cin>>u>>v>>w;
addedge(u,v,w);
// addedge(v,u,w); //无向图反向加边
}
}
void dfs(int start,int father){
for(int i=head[start];i!=0;i=nextE[i]){
//一直i=nextE[i],寻找与i同层级的边,即以now为起点的所有边
int v=to[i],w=weight[i];
if(v!=father){
// 1
// / \
// 2 3
// 如果有1->3和3->1两条边,1号点搜索到3号点,3号点又会回到1号点
// 无限循环,所以要判断3号点为头的边是否指向了父亲节点,或者标记
// 是否访问过
dfs(v,start);
}
}
}并查集
解决有关图每一部分之间联通性的问题
实现方法是用一颗树来将联通的节点串在一起,father[i]为i的上一级节点,如果要判断两个节点是否联通就判断他们的祖先节点是否相同,向集合里加入边时如果起点和终点在一个集合就无需操作,如果不在一个集合就把他们的祖先节点相连。
#define MAXN 100010*2
vector<int> father(MAXN);
void init(int n){
for(int i=0;i<n;i++){
father[i]=i;
}
}
int find(int u){
if(father[u]=u) return u;
else return find(father[u]);
}
void join(int u,int v){
u = find(u);
v = find(v);
if(u==v) return;
father[v]=u;
}
bool issame(int u,int v){
u = find(u);
v = find(v);
return u==v;
}路径压缩
并查集本质就是若干棵树,并查集的效率和这颗树的深度有关,由于我们只关注联通问题,可以将树里的所有节点都连在根节点下。只要修改find函数就可以,查询祖先节点时把他直接与祖先节点相连。但是路径压缩只在查询节点时才执行,如果只加入不查询,效率还是很低。
int find(int u){
return father[u]==u ? u : father[u]=find(father[u]);
}按秩合并
前面说了并查集的效率的树的深度有关,除了压缩路径,我们还可以在合并时将深度小的树合并到深度大的树中来尽可能减小树的深度,这样需要额外一个数组来保存每个节点的深度,只修改join函数就可以了。
void join(int u,int v){
u = find(u);
v = find(v);
if(u==v) return;
if(rank[u]<rank[v]){
father[u]=v;
}else if(rank[u]<rank[v]){
father[v]=u;
}else{
father[v]=u;
rank[u]++;
}
}将上述两种优化方法和在一起并查集的效率就很高了,但是因为路径压缩了,每个节点的秩并不准确,下面是并查集最终的代码
#define MAXN 100010*2
vector<int> father(MAXN);
vector<int> rank(MAXN);
void init(int n){
for(int i=0;i<n;i++){
father[i]=i;
rank[i]=0;
}
}
int find(int u){//路径压缩
return father[u]==u ? u : father[u]=find(father[u]);
}
void join(int u,int v){//按秩合并
u = find(u);
v = find(v);
if(u==v) return;
if(rank[u]<rank[v]){
father[u]=v;
}else if(rank[u]<rank[v]){
father[v]=u;
}else{
father[v]=u;
rank[u]++;
}
}
bool issame(int u,int v){
u = find(u);
v = find(v);
return u==v;
}最小生成树
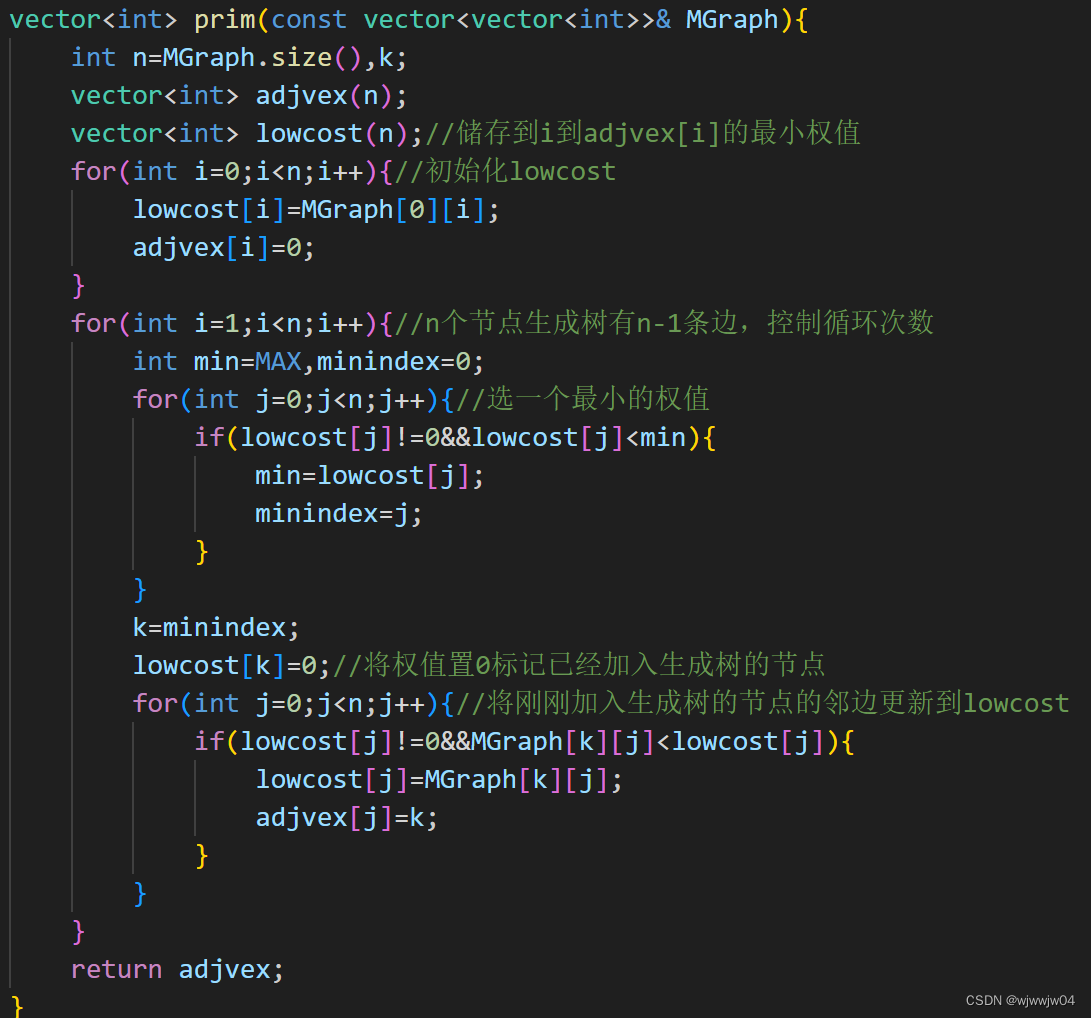
Prim算法
时间复杂度O(V^2)
kruskal算法
时间复杂度O(E)

最短路
Dijkstra算法
时间复杂度O(V^2)
vector<int> Dijkstra(const vector<vector<int>>& MGraph,int start){
int n=MGraph.size(),k=start;
vector<int> adjvex(n);
vector<int> lowcost(n,INT_MAX); //储存到start到i的最短路径权值
vector<int> visited(n,0); //标记到某节点的最短路径是否找到
lowcost[start]=0; //将到start的距离初始化为0,第一次循环
//找出的k就是start,相当于初始化
for(int i=1;i<=n;i++){ //每次找到一个最短路,一共需要n次循环
int min=MAX,k=0; //k储存最小值的下标
for(int j=0;j<n;j++){ //选一个最小的权值
if(visited[j]==0&&lowcost[j]<min){
min=lowcost[j];
k=j;
}
}
visited[k]=1; //标记节点访问过
for(int j=0;j<n;j++){ //将最短路更新
if(visited[j]==0&&MGraph[k][j]+min<lowcost[j]){
lowcost[j]=MGraph[k][j]+min;
adjvex[j]=k;
}
}
}
return adjvex;
}Dijkstra算法堆优化
时间复杂度O(E*logE)
struct MyCompare {
bool operator()(const pair<int,int>& a, const pair<int,int>& b) {
return a.second>b.second;
}
};//自定义比较函数
vector<int> dijkstra(int n,vector<vector<pair<int,int>>>& edges,int start){
vector<bool> visited(n+1,false);
vector<int> lowcost(n+1,INT_MAX);
priority_queue<pair<int,int>,vector<pair<int,int>>,MyCompare> q;
q.push(make_pair(start,0));
lowcost[start]=0;
while(!q.empty()){
pair<int,int> cur=q.top();q.pop();
int u=cur.first;
if(visited[u]==1) continue;
visited[u]=true;
for(auto temp:edges[u]){
int v=temp.first,w=temp.second;
if(visited[v]==0 && lowcost[u]+w<lowcost[v]){
lowcost[v]=lowcost[u]+w;
q.push(make_pair(v,lowcost[v]));
}
}
}
return lowcost;
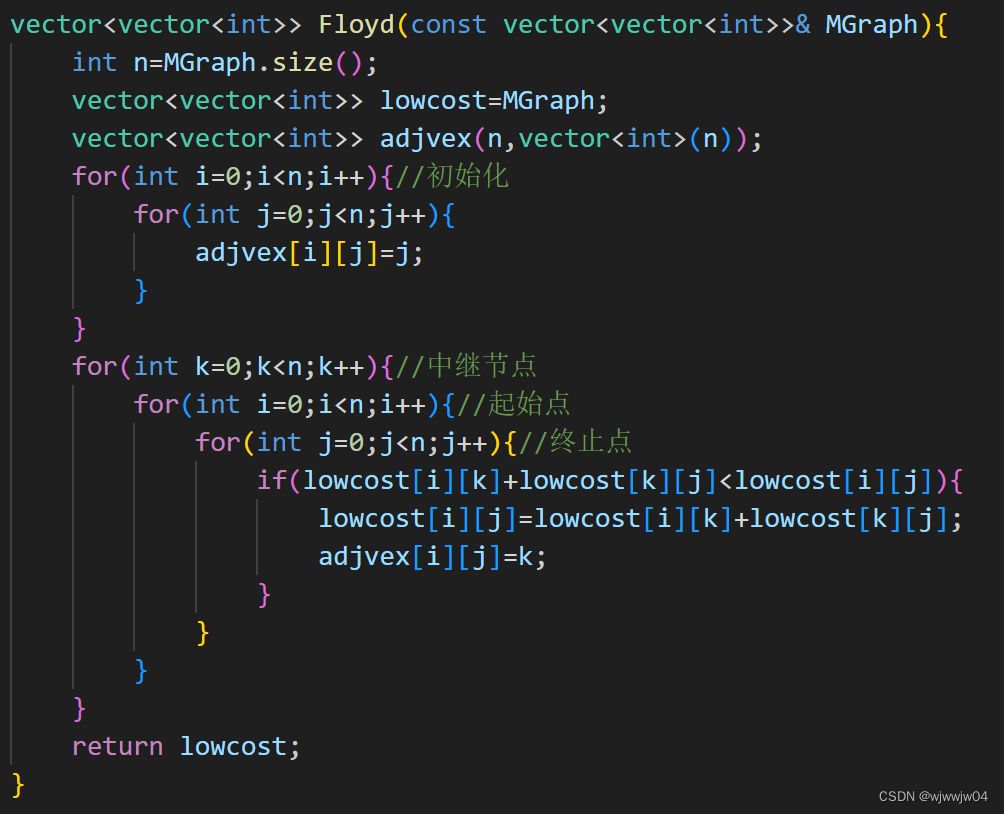
}Floyd算法
时间复杂度O(V^3)
可以求出所有点之间的最短路
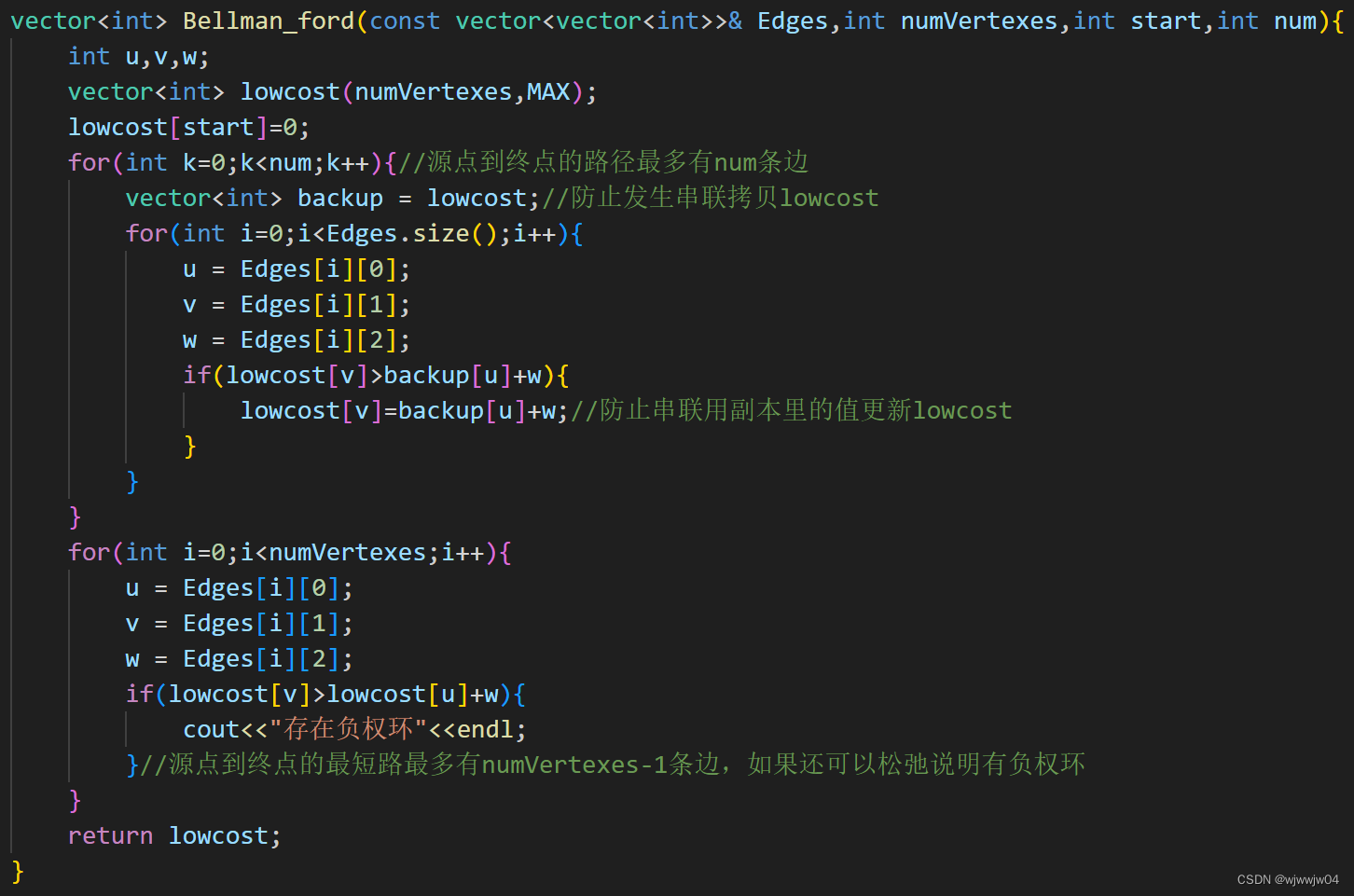
Bellman ford算法
时间复杂度O(V*E)
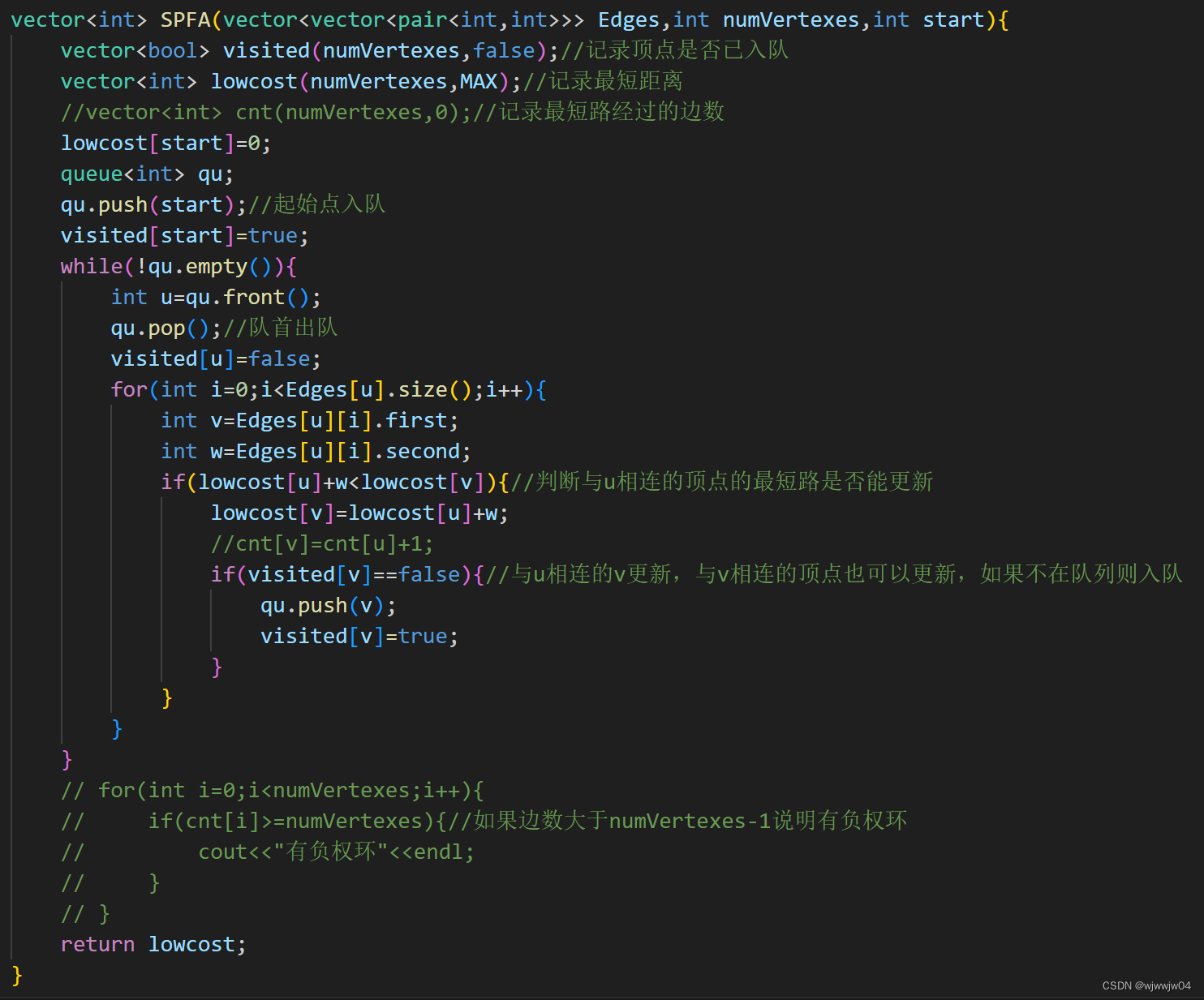
SPFA算法
最坏时间复杂度O(V*E)
欧拉回路
欧拉通路·:通过所有边的路径
欧拉回路:通过所有边且最后回到出发点的路径
无向图:
欧拉通路:存在两个度为奇数的顶点,这两个点分别是起点和终点
欧拉回路:所有顶点的度均为偶数
有向图:
欧拉通路:只有两个顶点入度不等于出度,其中一个点入度比出度小1,为起点。另一个点入度比出度大1,为终点。
欧拉回路:所有顶点的入度等于出度







 本文概述了图论中的关键概念,如并查集、Prim算法与Kruskal算法用于最小生成树的构建,以及Dijkstra、Floyd、Bellmanford和SPFA算法在求解最短路径问题中的应用。特别介绍了欧拉回路在无向图和有向图中的存在条件及其特点。
本文概述了图论中的关键概念,如并查集、Prim算法与Kruskal算法用于最小生成树的构建,以及Dijkstra、Floyd、Bellmanford和SPFA算法在求解最短路径问题中的应用。特别介绍了欧拉回路在无向图和有向图中的存在条件及其特点。














 2380
2380











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








