2023年优化算法之减法平均优化器，matlab代码直接复制，并与灰狼，粒子群算法比较...

“ 今天的主角是：2023年4月份新鲜出炉的优化算法，“减法平均优化器”，目前知网还搜不到。该算法原理简单，非常适合新手，算上初始化粒子，总共就4个公式。但是！重点来了，该算法原理虽然简单，但是寻优效果却是极好的。下面会将该算法与粒子群算法和灰狼算法进行对比。”

01

—

减法平均优化器原理

    减法优化器（Subtraction-Average-Based Optimizer，SABO）设计的基本灵感来自数学概念，如平均值、搜索代理位置的差异以及目标函数的两个值的差异符号。

• （1）算法初始化

粒子初始化公式和粒子群等大部分智能优化算法一样，就是在上下限值的范围内采用rand函数随机生成一堆粒子。

• （2）SABO数学模型

SABO算法引入了一个新的计算概念，“-v”，称为搜索代理B与搜索代理a的v−减法，定义如下：

是一个维度为m的向量，是一个[1，2]生成的随机数，F(A)和F(B)分别是搜索代理A和B的目标函数的值，sign是signum函数。

在SABO算法中，任何搜索代理Xi在搜索空间中的位移都是通过每个搜索代理Xj的“-v”减法的算术平均值来计算的。位置更新方式如下：

N是粒子的总数，ri是一个服从正态分布的随机值。

粒子位置替换公式，这个也与绝大多数算法一致。

SABO算法的数学模型如下：

SABO算法流程图如下：

02

—

SABO的寻优效果展示

依旧是在CEC2005函数上进行测试，算法设置迭代次数为1000次，种群个数为30个。

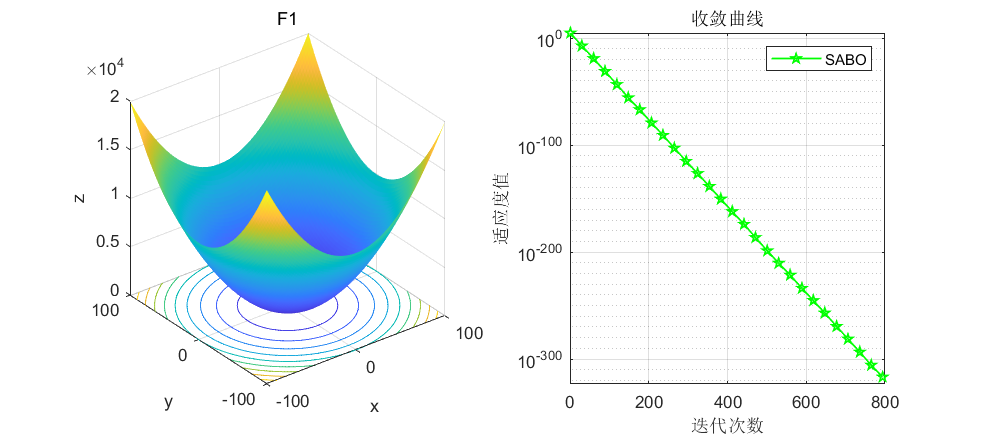
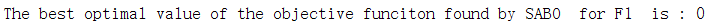
由这个F1函数可以看到，SABO算法在大约800次左右就寻优到了0。而其他算法最多也就是e-几百次方，很少有直接到0的。另外说一下，SABO算法由于原理简单，其运行速度是极快的，大家可以自行尝试哈。

接下来直接将SABO算法与灰狼算法和粒子群算法进行对比，SABO算法的好坏大家自行体会了。

03

—

SABO的MATLAB代码

function[Best_score,Best_pos,SABO_curve]=SABO(N,T,lo,hi,m,fitness)
lo=ones(1,m).*(lo);                              % Lower limit for variables
hi=ones(1,m).*(hi);                              % Upper limit for variables
%% INITIALIZATION
for i=1:m
    X(:,i) = lo(i)+rand(N,1).*(hi(i) - lo(i));                          % Initial population
end
for i =1:N
    L=X(i,:);
    fit(i)=fitness(L);
end
%%
for t=1:T  % algorithm iteration
   %%  update: BEST proposed solution
    [Fbest , blocation]=min(fit);
    if t==1
        xbest=X(blocation,:);                                           % Optimal location
        fbest=Fbest;                                           % The optimization objective function
    elseif Fbest<fbest
        fbest=Fbest;
        xbest=X(blocation,:);
    end
    %%
    DX=zeros(N,m);  
    for i=1:N
        %% based om Eq(4)
        for j=1:N
            I=round(1+rand+rand);
            for d=1:m
                DX(i,d)=DX(i,d)+(X(j,d)-I.*X(i,d)).*sign(fit(i)-fit(j));
            end
        end
        X_new_P1= X(i,:)+((rand(1,m).*DX(i,:))./(N));
        X_new_P1 = max(X_new_P1,lo);
        X_new_P1 = min(X_new_P1,hi);
        
        %% update position based on Eq (5)
        L=X_new_P1;
        fit_new_P1=fitness(L);
        if fit_new_P1<fit(i)
            X(i,:) = X_new_P1;
            fit(i) = fit_new_P1;
        end
        %%            
    end% end for i=1:N
    %%
    best_so_far(t)=fbest;
    average(t) = mean (fit);
    
end
Best_score=fbest;
Best_pos=xbest;
SABO_curve=best_so_far;
end

这里还是直接上核心代码，大家直接复制即可。

SABO算法的文献，SABO的MATLAB代码，SABO算法与灰狼算法和粒子群算法的对比代码统统都打包好了，直接回复关键词免费获取。

后台回复关键词，获取代码：2023

觉得文章不错的，给作者留个赞吧！谢谢！