前言:好久没有学数学了
前几天loli给高一的讲课涉及到了本章内容,所以来普及一波
差分序列
基本概念
设
是一个序列,我们定义的(一阶)差分序列为:

很简单吧,就是我们经常使用的差分啊
但是我们在叙述ta的定义的时候,加了一个词:一阶
有一阶就有二阶,有二阶就有三阶~ppp阶啊:
ppp阶差分序列:
我们定义一个序列的0阶差分序列就是ta自己:
我们可以把一个序列的0~P阶差分序列优美的写成一个倒三角,俗称差分表:

∞ 例一
设序列为:hn=2∗n2+3∗n+1h_n=2*n^2+3*n+1hn=2∗n2+3∗n+1,这个序列的差分表?
1 6 15 28 45 66 91 ...
5 9 13 17 21 25 ...
4 4 4 4 4 ...
0 0 0 0 ...
在此例中,三阶差分序列全部由0组成,因此所有更高阶的差分序列都是由0组成的
现在我们支持,如果一个序列的通项是n的p次多项式,那么 (p+1)阶差分就都是0 ,这种情况下,我们可以把第一行0
后的所有0行删去
定理一
设序列的通项时n的p次多项式,即:
则对所有的
上面我们提出了一个很简单的定理(证明不是很简单,这里就不呈现给大家啦)
性质一
现在假设gng_ngn,fnf_nfn分别是两个序列的通项,定义另一个序列如下:
hn=gn+fn(n>=0)h_n=g_n+f_n (n>=0)hn=gn+fn(n>=0)
则
更一般的,我们可以归纳出:

如果c和d是常数,则对每一个整数p>=0,有:

我们把以上的内容叫做差分的线性性质
由此可以看到,序列Hn的差分表可以通过 ccc乘以gng_ngn的差分表的项并用ddd乘以fnf_nfn的差分表的项 ,然后将相应的项相加而得
∞ 例二
设gn=n2+n+1g_n=n^2+n+1gn=n2+n+1,fn=n2−n−2f_n=n^2-n-2fn=n2−n−2
gng_ngn的差分表:
1 3 7 13 21 ...
2 4 6 8 ...
2 2 2 ...
0 0 ...
fnf_nfn的差分表:
-2 -2 0 4 10 ...
0 2 4 6 ...
2 2 2 ...
0 0 ...
设hn=5n2−n−4h_n=5n^2-n-4hn=5n2−n−4,则hnh_nhn的差分表?
因为 hn=2gn+3fn=2(n2+n+1)+3(n2−n−2)=5n2−n−4h_n=2g_n+3f_n=2(n^2+n+1)+3(n^2-n-2)=5n^2-n-4hn=2gn+3fn=2(n2+n+1)+3(n2−n−2)=5n2−n−4
则hnh_nhn的差分表通过将第一个差分表的各项乘以2并将第二个差分表的各项乘以3然后对应相加,就可以得到结果了:
-4 0 14 38 72 ...
4 14 24 34 ...
10 10 10 ...
0 0 ...
差分表的对角线
我们还是继续研究差分表:

图中,我圈出了一列数据,这些数据的下脚标都是0
这一列就是第0条对角线
定理二
差分表的第0条对角线等于
c0,c1,c2,…,cp,0,0,0,…
这样序列的通项满足:
∞ 例三
设:hn=n3+3n2−2n+1h_n=n^3+3n^2-2n+1hn=n3+3n2−2n+1
计算差分我们得到:
1 3 17 49
2 14 32
12 18
6
因为hnh_nhn是nnn的三次多项式,所以ta的差分表的第0条对角线就是:1,2,12,6,0,0,…
因此,根据定理二,hn就可以改写为:

我们为什么要用这种方式改写通项公式呢
其中一个原因就是求解部分和

其中:

这个是怎么来的呢:

因此原式可化为:

定理二
一个序列:$h_0,h_1,h_2,h_3,…,h_n,… $ 的第0条差分表的第0条对角线
c0,c1,c2,c3,...,cp,0,0,...c_0,c_1,c_2,c_3,...,c_p,0,0,...c0,c1,c2,c3,...,cp,0,0,...
则:
∞ 例四
求前n个正整数的4次方和
设:hn=n4hn=n^4hn=n4
计算差分序列:
0 1 16 81 256
1 15 65 175
14 50 110
36 60
24
则第0条对角线就是:0,1,14,36,24,0,0,…
那么我们就有式子:

Stirling数
基本概念
之前我们简单的介绍了一下差分序列
假如我们现在有一个序列:hn=nph_n=n^phn=np
记ta的第0条对角线为:c(p,0),c(p,1),c(p,2),…,c(p,p),0,0,…
现在我们引入

这个叫做第二类Stirling数
(不要问ta为什么叫第二类,我为什么不先讲第一类。。。)
现在我们提出第二类StirlingStirlingStirling数的递推公式:
####定理三
如果1<=k<=p−11<=k<=p-11<=k<=p−1,则
我们先感性的理解一下:

S(p,k)S(p,k)S(p,k)都是这样得到的:把这一项所处行的直接上方的元素乘以k,然后再把结果加上该项的直接左边的项
这个怎么理解呢?
定理四
第二类StirlingStirlingStirling数 S(p,k)S(p,k)S(p,k) 计数的是把ppp元素划分到kkk个不可区分的盒子且没有空盒子的划分个数
证明:
首先,我们先解释在当前情况下不可区分意味着什么
说这些盒子是不可区分的,指的是我们不能说出一个盒子与另一个盒子的差异,ta们看起来是一样的
例如,如果某个盒子里装的是a,b,c,那么ta究竟在哪一个盒子并不重要
唯一重要的是各个盒子里装的是什么,而不管哪个盒子装了什么
考虑将前ppp个正整数1,2,...,p1,2,...,p1,2,...,p的集合作为要被划分的集合
把{ 1 , 2 , 3 , … , p }分到k个非空且不可区分的盒子有两种类型:
- 那些使ppp自己单独在一个盒子的划分
- 那些使ppp不单独在一个盒子的划分,这样包含ppp的盒子就至少还包含一个元素
在第一种划分中,我们把ppp单独拿出来放在一个盒子里,
因为盒子都不可区分,所以ppp放在哪一个盒子里并不重要
那么就将 { 1 , 2 , 3 , … , p-1 } 分到k−1k-1k−1个盒子中
这就贡献了S(p−1,k−1)S(p-1,k-1)S(p−1,k−1)种方案
在第二种划分中,我们把ppp单独拿出来,由于ppp不单独在盒子里,
因此就得到将 { 1 , 2 , 3 , … , p-1 } 分到kkk个盒子中
大家可能认为,这样就贡献了S(p−1,k)S(p-1,k)S(p−1,k)种方案
不然
由于ppp的删除而产生的 { 1 , 2 , 3 , … , p-1 } 的划分A1,A2,A3,...,AkA_1,A_2,A_3,...,A_kA1,A2,A3,...,Ak产生于 { 1 , 2 , 3 , … , p } 的k个划分,即产生于:
A1∪p,A2,...,AkA_1∪{p},A_2,...,A_kA1∪p,A2,...,Ak
A1,A2∪p,...,AkA_1,A_2∪{p},...,A_kA1,A2∪p,...,Ak
.........
A1,A2,...,Ak∪pA_1,A_2,...,A_k∪{p}A1,A2,...,Ak∪p
换句话说,在删除ppp之后,我们无法告知ta来自于哪个盒子
在ppp取走后所有的盒子仍然是非空的,因此这个盒子可能是k个盒子中的任何一个
因此第二种划分就贡献了kS(p−1,k)kS(p-1,k)kS(p−1,k)种方案
原式得证
博主这个死鬼,为什么不介绍第一类StirlingStirlingStirling数???
那我们就给出第一类Stirling数的递推式
定理六
如果1<=k<=p-1,则
s(p,k)=(p−1)s(p−1,k)+s(p−1,k−1)s(p,k)=(p-1)s(p-1,k)+s(p-1,k-1)s(p,k)=(p−1)s(p−1,k)+s(p−1,k−1)
至于ta的组合意义有一点难理解
定理五
第一类StirlingStirlingStirling数 s(p,k)s(p,k)s(p,k)计数的是把p个对象排成k个非空循环序列的方法数
我们可以把定理叙述中的循环排列叫做圆圈








 本文介绍了差分序列的概念及应用,包括差分表的构造、差分表的对角线及其与序列通项的关系,并详细阐述了第二类Stirling数的定义、递推公式及其组合意义。
本文介绍了差分序列的概念及应用,包括差分表的构造、差分表的对角线及其与序列通项的关系,并详细阐述了第二类Stirling数的定义、递推公式及其组合意义。




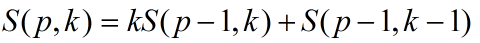
















 688
688

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








