三维凸包

和二维凸包类似，给定一堆三维空间中的点，包含ta们的最小凸多面体称为这些点的凸包

三维凸包的求法很多：

暴力法

枚举三个点组成的有向三角形（实际上是一个半平面），判断是否所有点都在这个三角形的同侧
复杂度：$O(n^4)$

卷包裹法

该算法的思想是先找到一条肯定在凸包上的边$P_iP_j$，
想象一张纸紧贴这条边，向左旋转，直到碰到一个点$P_k$，
然后以$P_kP_i$和$P_kP_j$为轴继续旋转

相比较来说，卷包裹法是一种比较具象的方法，然而仍有一些需要注意的问题：
首先就是起始边的选择，
一般先把点投影到z=0平面，求出二维凸包，
然后把二维凸包上的一条边作为三维凸包卷包裹的初始边
根据二维凸包的性质，不必真的做投影和凸包
只需要找到一个y坐标最小的点作为起点，到ta极角最小的点作为第二个点

但是，当“y坐标最小”和“极角最小”的选择不止一个的时候，以上算法很容易出错
另外，多点共面也是比较麻烦的问题

增量法

基本思想是把点依次加到凸包中，
初始时随机选两个点$P_1,P_2$，然后找一个不和这两个点共线的点$P_3$，再找一个不和以上三点共面的点$P_4$，组成初始凸包
然后依次考虑其他点$P_r$
如果这个点在当前凸包内，直接忽略
否则，想象该点变成了一个白炽灯，向四面八方散发光线
光线找到我们已经得到的凸包上，会形成亮面和暗面
删除亮面中的所有点（能被光线照射到）
然后把阴影边界上的所有点和$P_r$连接起来，其中每条边和$P_r$构成一个三角形

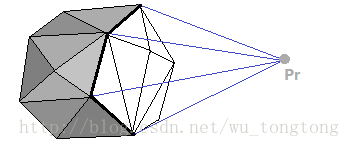
这个算法的简单实现方法是遍历所有面，判断是否可见
然后遍历所有边，判断是否在阴影边界上

然而光这样，我们还是没有办法代码实现
我们还需要考虑特殊情况（比如凸包上多点共面）
简单起见，实践中常常先把输入点进行微小扰动

注意

在记录面的时候
简单起见，假设所有面都是三角形，且三个点由右手定则确定的方向指向多边形的外部

右手定则：
有点类似右手螺旋定则

（即从外部看，三个顶点呈逆时针排布）
所以这些面上的三个点的排列顺序并不是任意的

bool vis[N][N];
struct node{
    double x,y,z;
    node (double xx=0,double yy=0,double zz=0)
    {
        x=xx;y=yy;z=zz;
    }
}

node operator +(node A,node B) {return node(A.x+B.x,A.y+B.y,A.z+B.z);}
node operator -(node A,node B) {return node(A.x-B.x,A.y-B.y,A.z-B.z);}
node operator *(node A,double B) {return node(A.x*B,A.y*B,A.z*B);}
node operator /(node A,double B) {return node(A.x/B,A.y/B,A.z/B);}

double Dot(node A,node B) {
    return A.x*B.x+A.y*B.y+A.z*B.z;
}

node Cross(node A,node B) {
    return node(A.y*B.z-A.z*B.y,A.z*B.x-A.x*B.z,A.x*B.y-A.y*B.x);
}

struct Face()    //面
{
    int v[3];
    node normal(node &P) const {
        return Cross(P[v[1]]-P[v[0]],P[v[2]]-P[v[0]]);
    }
    int cansee(node &P,int i) const {                 //混合积 
        return Dot(P[i]-P[v[0]],normal(P)) >0? 1:0;
    }
}

//增量法
//调用前需要对输入点进行微小扰动 
vector<Face> TuB3D(node* P,int n){
    vector<Face> cur;                 //面 
    //扰动后，前三个点不共线 
    cur.push_back((Face){{0,1,2}});   //加入初始面 
    cur.push_back((Face){{2,1,0}});   //排列顺序不同，半空间不同 
    for (int i=3;i<n;i++)             //依次加入每个点 
    {
        vector<Face> nxt;
        //计算每条边左边的可见性 
        for (int j=0;j<cur.size();j++)
        {
            Face& f=cur[j];
            int res=f.cansee(P,i);
            if (!res) nxt.push_back(f);   //阴影中的保留 
            for (int k=0;k<3;k++) vis[f.v[k]][f.v[(k+1)%3]]=res;
        }
        for (int j=0;j<cur.size();j++)
            for (int k=0;k<3;k++)
            {
                int a=cur[j].v[k],b=cur[j].v[(k+1)%3];
                if (vis[a][b]!=vis[b][a]&&vis[a][b])   //ab是分界线，左边可见 
                    nxt.push_back((Face){{a,b,i}});    //新的面
            }
        cur=nxt;
    }
    return cur;
}

//微小扰动 
double rand0(){return rand()/(double)RAND_MAX;}
double randeps(){return (rean0()-0.5)*eps;}  //-eps/2到eps/2的随机数 

代码的可读性还是比较高的