【高等数学】第 2 讲 两个重要的极限定理

• 作者： wugenqiang
• 学习笔记：https://notebook.js.org/
• 微信公众号：码客 E 分享（ID：enjoytoshare）

文档后续更新地址：【高数基础】

第 2 讲 两个重要的极限定理

---

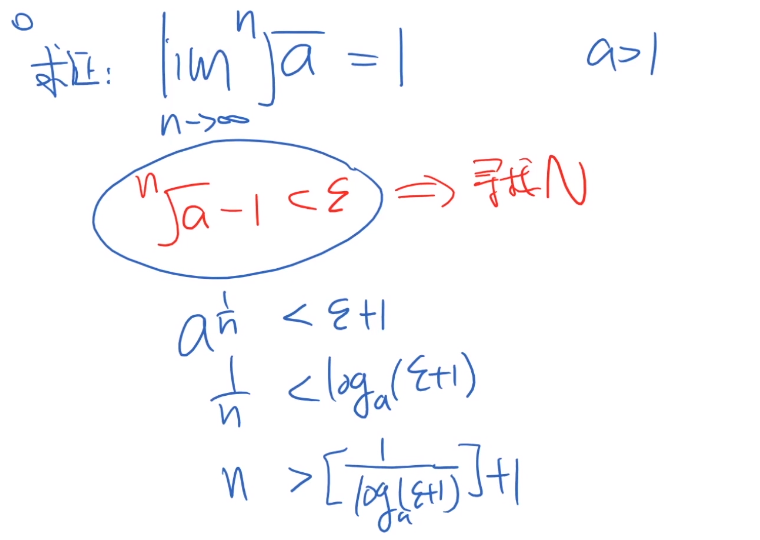
两个重要极限：

• $\underset{n\to \infty }{\lim }(1+\frac{1}{n}{)}^n=e$
• $\underset{x\to 0}{\lim }\frac{sinx}{x}=1$

2.1 第一个重要极限定理的证明

• 【证明】$\underset{n\to \infty }{\lim }(1+\frac{1}{n}{)}^n=e$

先证明极限存在：

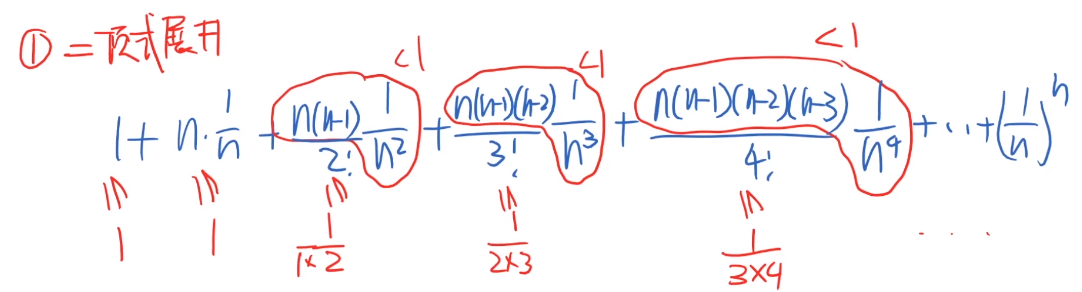
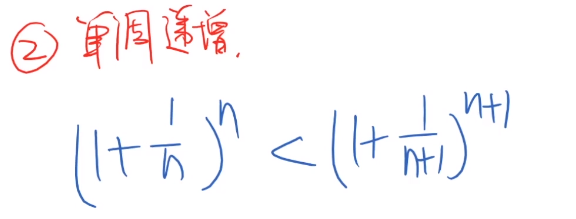
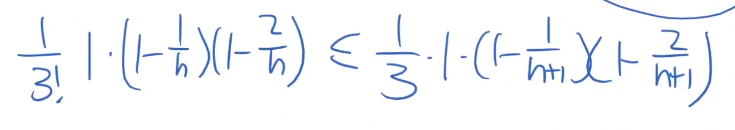
• 计算机表示：

2.2 夹逼定理

• 引理：夹逼定理

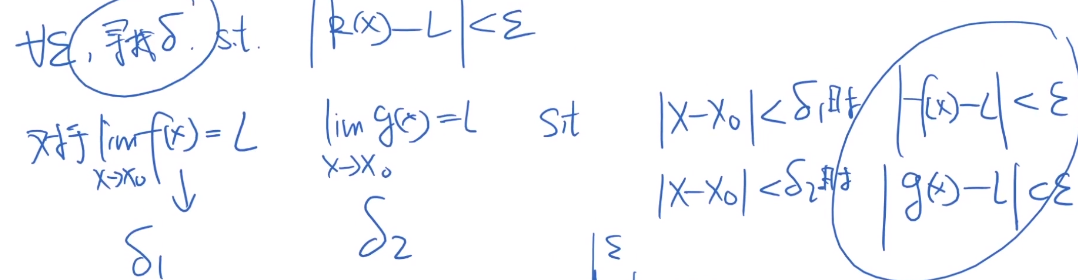
2.3 第二个重要极限定理的证明

• 【证明】$\underset{x\to 0}{\lim }\frac{sinx}{x}=1$

使用夹逼定理来证明