文章原稿
https://gitee.com/fakerlove/fundamentals-of-compiling
文章目录
7. 语法制导的语义计算
7.1 基本概念
语义分析是上下文有关的,目前较为常见的是用属性文法来描述程序语言语义,并采用语法制导翻译的方法完成对语法成分的翻译工作。
1) 属性文法
- 属性文法,也称属性翻译文法
- Knuth在1968年提出
- 以上下文无关文法为基础
在文法G[S]的基础上,为文法符号关联有特定意义的属性,并为产生式关联相应的语义动作或条件谓语,称之为属性文法,并称文法G[S]为之的基础文法。
属性文法AG是一个四元式,即AG = (G, A, R, B):G是上下文无关文法,A是属性的有限集合,R是语义规则式的有限集合,B是样式的有限集合。
例子:
产生式 语义动作 S -> ABC {B.in_num := A .num; C.in_num := A .num; if (B.num=0 and (C.num=0) then print(“Accepted!” ) else print(“Refused!” ) } A -> A1a { A.num := A1.num + 1 } A -> ε { A.num := 0 } B -> B1b { B1.in_num := B.in_num; B.num := B1.num-1 } B -> ε { B.num := B.in_num } C -> C1c { C1.in_num := C.in_num; C.num := C1.num-1 } C -> ε { C.num := C.in_num }
2)两种属性:
1. 综合属性
用于“自下而上”传递信息
对关联于产生式 A -> α 的语义规则 b:=f(c1, c2, …, ck) ,如果 b 是 A的某个属性, 则称 b 是 A 的一个综合属性 。
- 自下而上传递信息
- 语法规则:根据右部候选式中的符号的属性计算左部被定义符号的综合属性
- 语法树:根据子结点的属性和父结点自身的属性计算父结点的综合属性

2. 继承属性
用于“自上而下”传递信息
对关联于产生式 A-> α 的语义规则b:=f(c1, c2, …, ck),如果 b 是产生式右部某个文法符号 X 的某个属性,则称 b 是文法符号 X 的一个继承属性。
例子:
在上例的属性文法中A .num,B.num 和 C.num 是综合属性值,而B.in_num 和 C.in_num 是继承属性值。比如在产生式
C -> C1c中,C1.in_num 是产生式右部符号C1的属性,由产生式左部符号C的in_num 属性确定,所以它是继承属性,“自上而下”的传递信息;C.num 是产生式左部符号C的属性,由产生式右部符号C1的num属性确定,所以它是综合属性,“自下而上”的传递信息。
3) 带标注语法分析树
即在语法树的基础上,将原来的非终结符结点修改为综合属性的赋值。
下面是一个简单表达式文法G[S]的一个仅含综合属性的属性文法(开始符号为S)
S→E{print(E.val)}
E→E1+T{E.val:=E1.val+T.val}
E→T{E.val:=T.val}
T→T1∗F{T.val:=T1.val×F.val}
T→F{T.val:=F.val}
F→(E){F.val:=E.val}
F→d{F.val:=d.lexval}
其中d.lexvald.lexval表示数值,E.val,T.val,F.val都为综合属性
现在要给表达式3∗(5+4)构造语法树和带标注语法分析树:
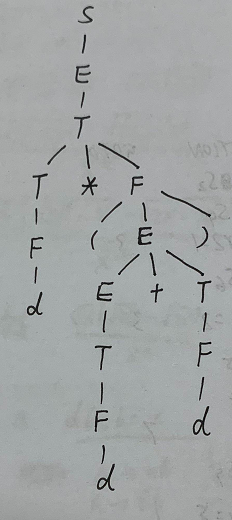

下面则是一个包含综合属性、继承属性的属性文法:
E→TR{R.in:=T.val;E.val:=R.val}
R→+TR1{R1.in:=R.in+T.val;R.val:=R1.val}
R→−TR1{R1.in:=R.in−T.val;R.val:=R1.val}
R→ε{R.val:=R.in}
T→num{T.val:=lexval(num)}
其中lexval(num)表示从词法分析程序得到的常数值。
可见E.val,T.val,R.val都为综合属性,R.in为继承属性
现在要给表达式3+4−5构造语法树和带标注语法分析树:
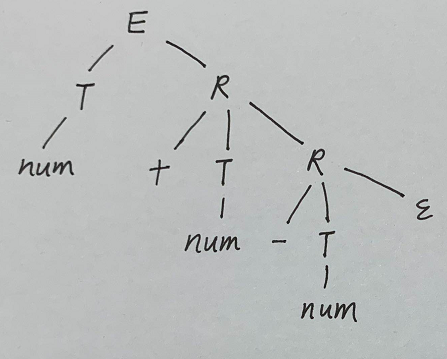

S-属性文法
只包含综合属性的属性文法。
L-属性文法
可以包含综合属性,也可以包含继承属性。但产生式右端某文法符号的继承属性的计算只取决于该符号左边文法符号的属性(对于产生式左边文法符号,只能是继承属性)。
4) 语义计算模型
- 属性文法:侧重于语义计算规则的定义
- 翻译模式:侧重于语义计算过程的定义
7.2 基于属性文法的语义计算
按照语义规则进行属性计算的3种方法
- 依赖图
- 树遍历
- 一遍扫描
7.2.1 语义子程序
1) 作用
用来描述一个产生式所对应的翻译工作。
– 如:改变某些变量的值;查填各种符号表;发现并报告源程序错误;产生中间代码等。
• 注:这些翻译工作很大程度上决定了要产生什么形式的中间代码。
2) 写法
语义子程序写在该产生式后面的花括号内。X →α {语义子程序1}
注:在一个产生式中同一个文法符号可能出现多次,
但他们代表的是不同的语义值,要区分可以加上角标。
如:E →E(1)+E (2)
3) 语义值
为了描述语义动作,需要为每个文法符号赋予不同的语义值:类型、地址、代码值等
4) 语义栈
-
各个符号的语义值放在语义栈中
当产生式进行归约时,需对产生式右部符号的语义值进行综合,其结果作为左部符号的语义值保存到语义栈中。
-
下推栈包含3部分:
状态栈、符号栈和语义栈
注:语义栈与状态栈和符号栈是同步变化的。
5) 例题
| 产生式 | 语义子程序 |
|---|---|
| S` →E | {PRINT E•VAL} |
| E →E(1)+E(2) | {E•VAL= E (1) •VAL +E(2) •VAL } |
| E →E (1)*E(2) | {E•VAL= E (1) •VAL *E(2) •VAL } |
| E →(E (1)) | {E•VAL= E (1) •VAL } |
| E → i | {E•VAL= LEXVAL } |
注:LEXVAL指的是词法分析送来的机内二进制整数。
7.2.2 依赖图
通过寻找属性之间的依赖关系,来确定属性计算的先后顺序,选择相应的语义规则,完成语义计算。
- 在一棵语法树中的结点的继承属性和综合属性之间的相互依赖关系可以由依赖图(有向图)来描述。
- 为每一个包含过程调用的语义规则引入一个虚综合属性b,这样把每一个语义规则都写成b :=f(c 1,c 2…c k)的形式
- 依赖图中为每一个属性设置一个结点,如果属性b依赖于属性c,则从属性c的结点用一条有向边连到属性b的结点。E→E1+E2 E.val := E1.val+E2.val[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aO72x15M-1621078687584)(picture/20200423152444984.png)]
- 依赖图的构建算法
//第一遍循环
for (结点 n : 语法树){
for(文法符号属性 a : n){
在依赖图中为a建立结点;
}
}
//第二遍循环
for (结点 n : 语法树){
for(语义规则 b : n){
//语义规则的形式为 b := f(c1,c2,...,ck)
//ci为b所依赖的属性
for(依赖属性 c: b){
构造从 c 指向 b 的有向边;
}
}
}
12345678910111213141516
- 对于属性文法:
| 产生式 | 语义规则 |
|---|---|
| D→TL | L.in := T.type |
| T → int | T.type := integer |
| T → real | T.type := real |
| T→T1*F | T.val := T1.val*F.val |
| L → L1,id | L1.in := L.in addtype(id.entry, L.in) |
| L → id | addtype(id.entry, L.in) |
语句 real id1,id2,id3的依赖图可以画成:

注意⑦⑨⑩是虚拟结点
- 良定义的属性文法
- 如果一属性文法不存在属性之间的循环依赖关系,则称该文法为良定义的
- 一个依赖图的任何拓扑排序都给出一个语法树中结点的语义规则计算的有效顺序
- 属性的计算次序
- 基础文法用于建立输入符号串的语法分析树
- 根据语义规则建立依赖图
- 根据依赖图的拓扑排序,得到计算语义规则的顺序输入串→语法树→依赖图→语义规则计算次序
7.2.3 树遍历
通过树遍历的方法计算属性的值
- 假设语法树已建立,且树中已带有开始符号的继承属性和终结符的综合属性
- (不需要建立依赖图)以某种次序遍历语法树,直至计算出所有属性
- 深度优先,从左到右的遍历输入串→语法树→遍历语法树计算属性
树遍历算法
while(还有未被计算的属性){
VisitNode(S);//S 是开始符号
}
//从根节点开始递归计算属性
void VisitNode(Node N){
if(N是非终结符){
//N的继承属性应该已经被计算出或者由编译器提供
//假定当前产生式是 N-> X1 X2 ... Xm,共m项
for(int i=1;i<=m;i++){
if(Xi 是非结符){
计算Xi 中能够计算的继承属性;
VisitNode(Xi);
计算Xi 中能够计算的综合属性;
}
}
计算N中能够计算的综合属性;
}
}
12345678910111213141516171819
树遍历示例
反复调用VisitNode(S)直到所有继承属性和综合属性都能被计算出来或者不再有更多的属性可以被计算为止。
第一次调用可以计算出Z.h=0和Z.g=1
第二次调用可以计算出X.c=1、X.d=2和S.b=0
第三次调用可以计算出Y.e=0和Y.f=0

请直接观看视频。
7.2.4 一遍扫描
- 在语法分析的同时计算属性值
- 所采用的语法分析方法
- 属性的计算次序
- 所谓语法制导翻译法,直观上说就是为文法中每个产生式配上一组语义规则,并且在语法分析的同时执行这些语义规则
- 语义规则被计算的时机
- 自上而下分析,一个产生式匹配输入串成功时
- 自下而上分析,一个产生式被用于进行归约时
- 在语法分析的同时计算属性值
- 适用于 S-属性文法 / L-属性文法
抽象语法树AST
抽象语法树(Abstract Syntax Tree,AST),在语法树中去掉那些对翻译不必要的信息,从而获得更有效的源程序中间表示
3*5+4:

建立表达式的抽象语法树
| 函数声明 | 作用 |
|---|---|
mknode(op, left, right) | 建立一个运算符号结点,标号是op, 两个域left和right分别指向左子树和右子树 |
mkleaf(id, entry) | 建立一个标识符结点,标号为id, 一个域entry指向标识符在符号表中的入口 |
mkleaf(num, val) | 建立一个数结点,标号为num, 一个域val用于存放数的值 |
运用以上函数,可以写出以下产生式的语义规则:
| 产 生 式 | 语 义 规 则 |
|---|---|
| E→E1+T | E.nptr := mknode(‘+’, E1.nptr, T.nptr ) 注意:此时我们认为E1和T已经被构建成了某一语法子树的根节点 |
| E→E1-T | E.nptr := mknode(‘-’, E1.nptr, T.nptr ) |
| E→T | E.nptr := T.nptr |
| T→ (E) | T.nptr := E.nptr 括号对于计算是多余的 |
| T→id | T.nptr := mkleaf ( id, id.entry ) |
| T→num | T.nptr := mkleaf ( num, num.val ) |
显然这种抽象语法树特别适合于自下而上的属性计算。
a - 4 + c对应的抽象语法树如下:

总结
了解综合属性和继承属性。已知属性文法和输入符号串,构建语法树和带标注语法分析树。
属性 描述文法符号的类型、值等有关的一些信息,它可以被计算或传递。
语义动作 指产生式相关联的指定操作
条件谓词 指产生式关联的接受条件,或者根据该条件谓词决定做什么语义动作
语义规则集 通常是产生式关联的一组语义规则,每个语义规则可以是一个语义动作或条件谓词。
属性attatt可以与某个文法符号aa关联,用a.atta.att来表示这种关联
现有一文法:
E→T1+T2∣T1&&T2
T→num∣true∣false
将上面的文法描述为类型检查的属性文法:
E→T1+T2{T1.type=int&&T2.type=int}
E→T1&&T2{T1.type=bool&&T2.type=bool}
T→num{T.type=int
T→true{T.type=bool}
T→false{T.type=bool}
























 3197
3197

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








