HMM算法-python实现

HMM 定义

设Q是所有可能的状态的集合，V是所有可能观测的集合

Q = { q 1 , q 2 , . . . , q n } , V = { v 1 , v 2 , . . . , v m } Q=\{q_1, q_2, ..., q_n\} ,V=\{v_1, v_2, ..., v_m\} Q={q1​,q2​,...,qn​},V={v1​,v2​,...,vm​}

其中n是可能的状态数，m是可能的观测数。

I是长度为t的状态序列，O是对应的观测序列

I = { i 1 , i 2 , . . . , i t } , O = { o 1 , o 2 , . . . , o t } I=\{i_1, i_2, ..., i_t\} ,O=\{o_1, o_2, ..., o_t\} I={i1​,i2​,...,it​},O={o1​,o2​,...,ot​}

A是状态转移矩阵

$$A=[a_{ij}{]}_{N\ast N}$$

对于I说，
$$a_{ij}=P(i_{t+1}=q_j|i_t=q_i)$$

B是观测矩阵

$$B=[b_i(k){]}_{N\ast M}$$

$$b_i(k)=P(o_t=v_k|i_t=q_i)$$

$\pi$是初始状态概率向量，则HMM模由$\pi$，A，B决定
$$\lambda =(A,B,\pi )。$$

• 齐次马尔科夫链假设。即任意时刻的隐藏状态只依赖于它前一个隐藏状态。
• 观测独立性假设。即任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态，
  

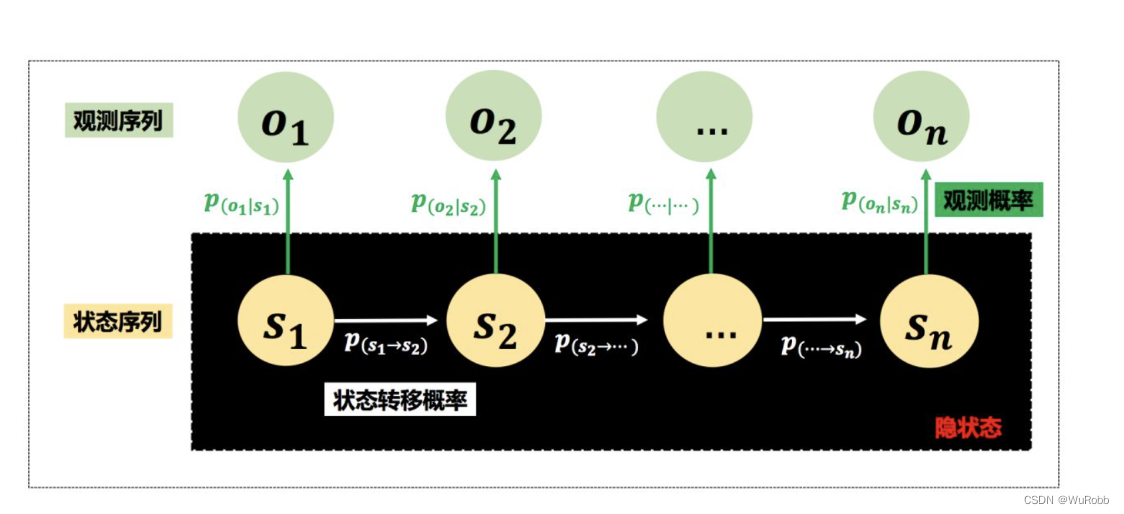
HMM的一个例子

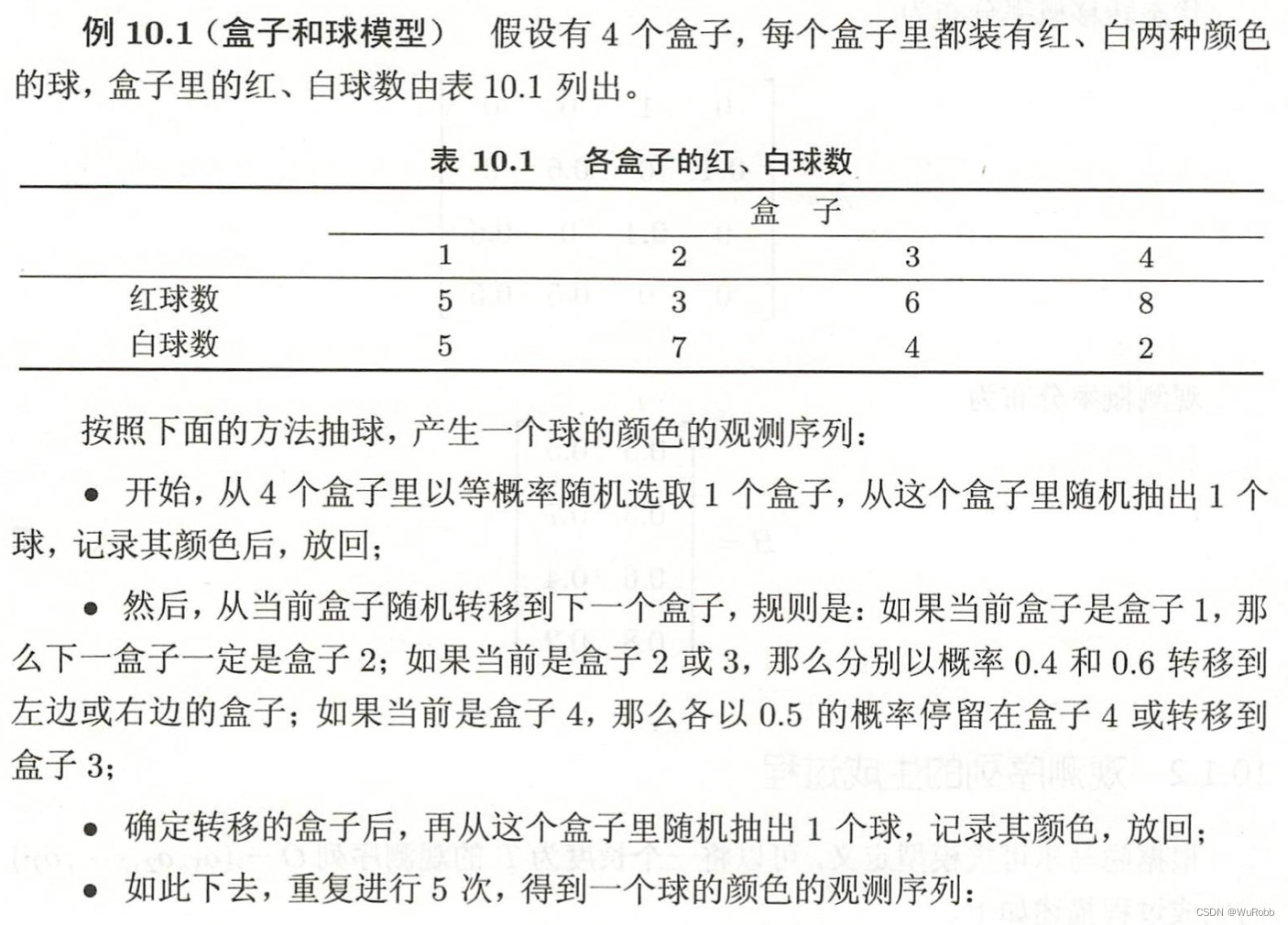
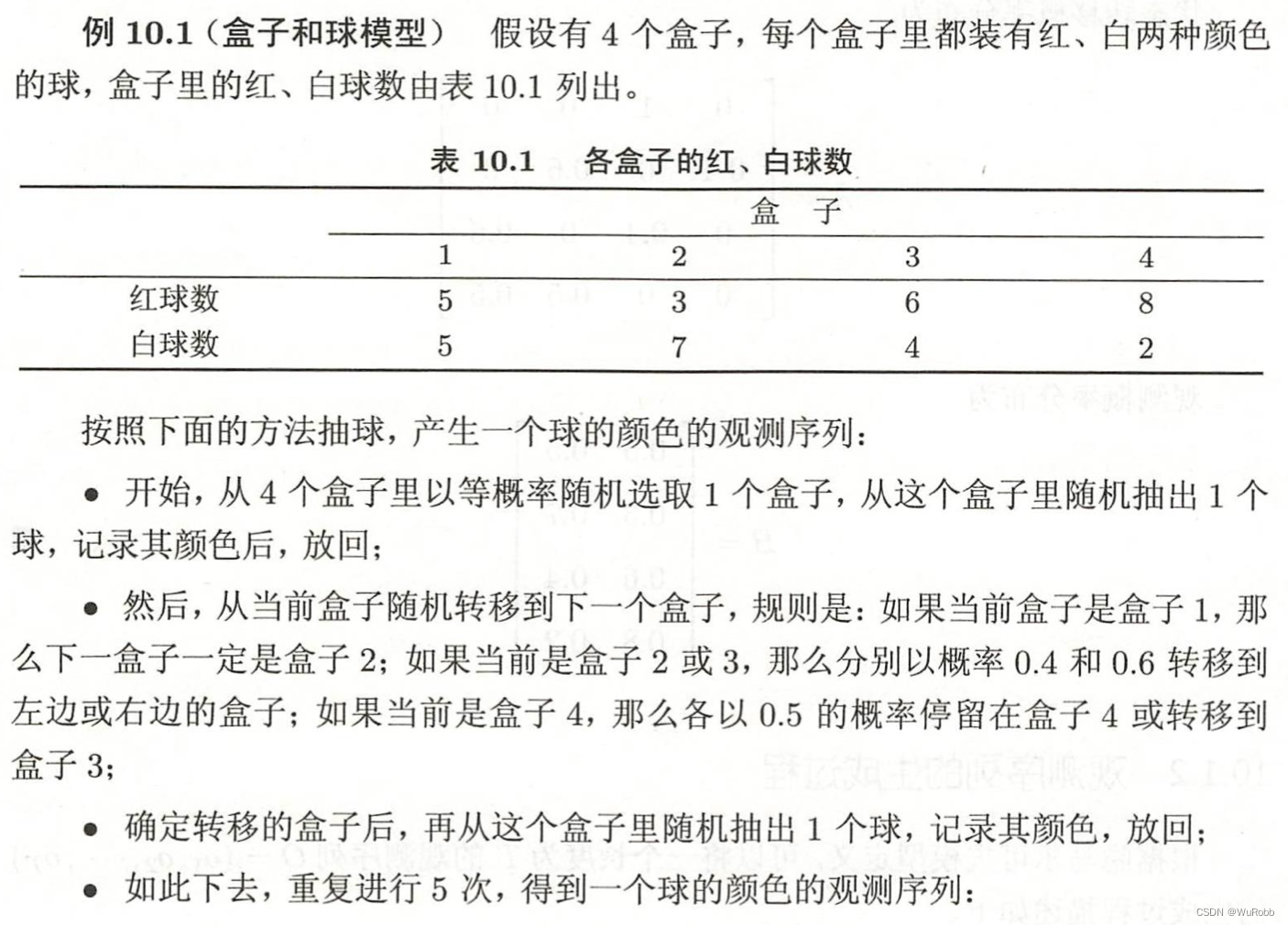
盒子所对应的状态集合为：

Q = { 盒子 1 ，盒子 2 ，盒子 3 ，盒子 4 } Q = \{盒子1， 盒子2， 盒子3， 盒子4\} Q={盒子1，盒子2，盒子3，盒子4}

观测合集为：
V = { 红，白 } V = \{红， 白\} V={红，白}

初始概率矩阵为：
π = { p ( 盒子 1 ) = 0.25 ， p ( 盒子 2 ) = 0.25 , p ( 盒子 3 ) = 0.25 , p ( 盒子 4 ) = 0.25 } \pi = \{p(盒子1) = 0.25， p(盒子2) = 0.25,p(盒子3) = 0.25,p(盒子4) = 0.25\} π={p(盒子1)=0.25，p(盒子2)=0.25,p(盒子3)=0.25,p(盒子4)=0.25}

状态转移矩阵为：
$$A=\left[\begin{array}{lcccc}& 盒子1& 盒子2& 盒子3& 盒子4\\ 盒子1& 0& 1& 0& 0\\ 盒子2& 0.4& 0& 0.6& 0\\ 盒子3& 0& 0.4& 0& 0.6\\ 盒子4& 0& 0.4& 0.5& 0.5\end{array}\right]$$

观测概率分布为：
$$B=\left[\begin{array}{ccc}& 红球& 白球\\ 盒子1& 0.5& 0.5\\ 盒子2& 0.3& 0.7\\ 盒子3& 0.6& 0.4\\ 盒子4& 0.8& 0.2\end{array}\right]$$

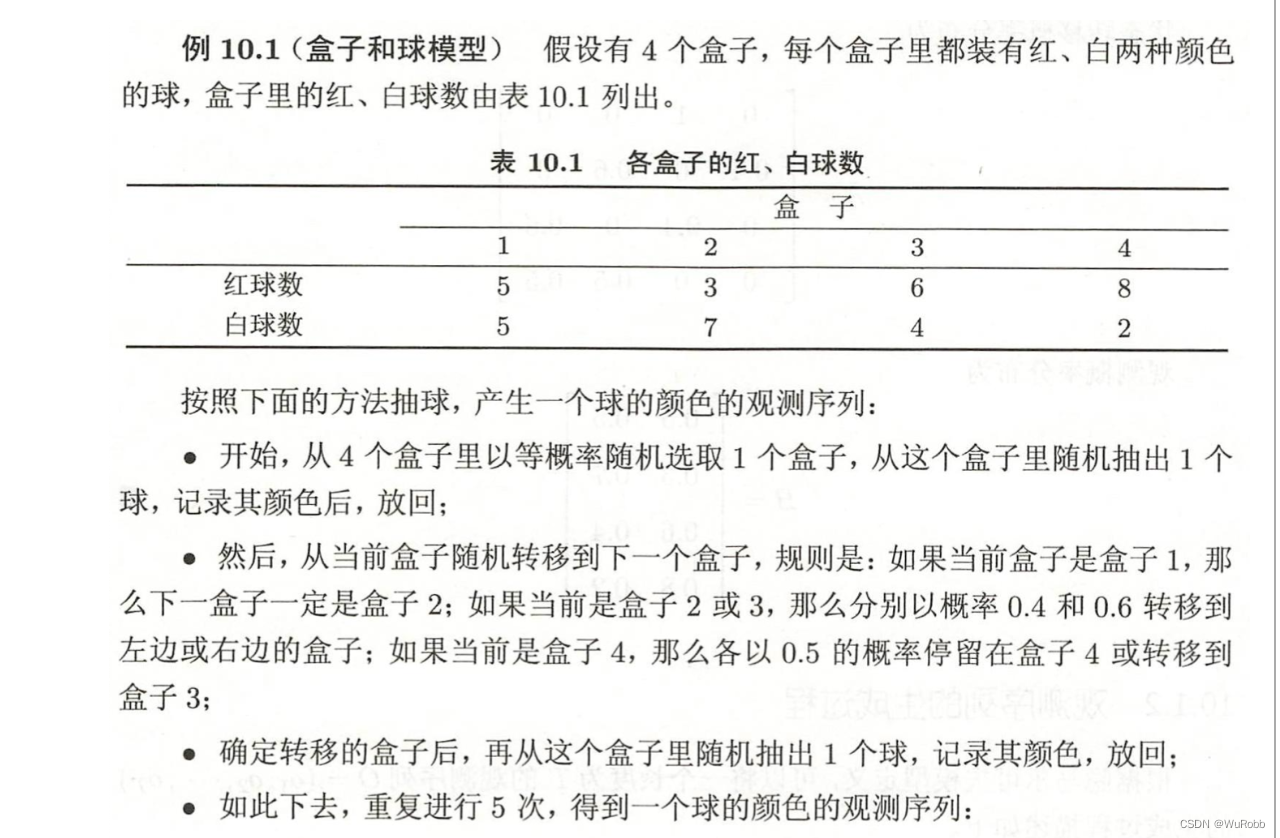
观测序列的生成过程

概率计算算法

• 直接计算法

状态序列 I = { i 1 , i 2 , . . . , i t } I=\{i_1, i_2, ..., i_t\} I={i1​,i2​,...,it​}的概率是：

$$P(I|\lambda )={\pi }_{i_1}\cdot a_{i_1{i}_2}\cdot \cdot \cdot a_{i_{t-1}{i}_t}$$

对该序列来说，观测序列 O = { o 1 , o 2 , . . . , o t } O=\{o_1, o_2, ..., o_t\} O={o1​,o2​,...,ot​}的概率为:

$$P(O|I,\lambda )=b_{i_1}(o_1)\cdot \cdot \cdot b_{i_t}(o_t)$$

O和I的联合概率：
$$P(O,I｜\lambda )=P(I|\lambda )P(O|I,\lambda )$$

则
P ( O ∣ λ ) = ∑ I P ( I ∣ λ ) P ( O ∣ I , λ ) = ∑ { i 1 , i 2 , . . . , i t } π i 1 ⋅ a i 1 i 2 ⋅ ⋅ ⋅ a i t − 1 i t ⋅ b i 1 ( o 1 ) ⋅ ⋅ ⋅ b i t ( o t ) \begin{align} P(O|\lambda) = &\sum_IP(I|\lambda)P(O|I,\lambda)\\ =& \sum_{\{i_1, i_2, ..., i_t\}}\pi_{i_1}·a_{i_1i_2}···a_{i_{t-1}i_t}·b_{i_1}(o_1)···b_{i_t}(o_t) \end{align} P(O∣λ)==​I∑​P(I∣λ)P(O∣I,λ){i1​,i2​,...,it​}∑​πi1​​⋅ai1​i2​​⋅⋅⋅ait−1​it​​⋅bi1​​(o1​)⋅⋅⋅bit​​(ot​)​​

该算法时间复杂度太高，采用前向后向算法

前向算法

• 1.初始值

$${\alpha }_1(i)={\pi }_i{b}_i(o_1)$$

• 2.递推

$${\alpha }_{t+1}(i)=[\sum _{j=1}^N{\alpha }_t(j)a_{ji}]b_i(o_{t+1})$$

• 3.中止
  $$P(O|\lambda )=\sum _{i=1}^N{\alpha }_t(i)$$

import numpy as np

O = ['红', '白', '红']
A = np.array([[0.5, 0.2, 0.3],
              [0.3, 0.5, 0.2],
              [0.2, 0.3, 0.5]])
B = np.array([[0.5, 0.5, ],
              [0.4, 0.6, ],
              [0.7, 0.3, ]])
pi = np.array([0.2,0.4,0.4])

# 前向算法计算
# 观察序列编码
O = [0, 1, 0, 1, 1]
def hmm_forward(O, A, B, pi):
    t = len(O)  
    # 第一步 初值
    a_t = pi*B[:,O[0]]
    
    # 递推计算
    for t1 in range(1, t):
        a_t = np.sum(a_t*A.T,axis=1)*B[:,O[t1]]
    
    # 中止
    return np.sum(a_t)

hmm_forward(O,A,B,pi)

# 输出：0.028486459399999997

后向算法

def hmm_backward(O, A, B, pi):
    t = len(O)  
    # 第一步 定义T时刻B
    b_t = np.array([1 for i in range(A.shape[0])])
    
    # 递推计算
    for t1 in range(t-1, 0, -1):
        b_t = np.sum(A*B[:, O[t1]]*b_t, axis = 1)
    
#     中止
    return np.sum(pi*b_t*B[:, O[0]])

hmm_backward(O,A,B,pi)

# 输出 0.028486459399999997

预测算法

贪心算法

贪心算法，取每个时间点最大的概率

$$i_t^{\ast }=arg\underset{1\le i\le N}{\max }{\alpha }_t(i){\beta }_t(i)$$

def optimized_path(O, A, B, pi):
    t = len(O)  
    # 第一步 初值
    a_t = pi*B[:,O[0]]
    b_t = np.array([1 for i in range(A.shape[0])])
    
    b_t_his = [b_t]
    a_t_his = [a_t]
    
    # a_t历史记录
    for t1 in range(1, t):
        a_t = np.sum(a_t*A.T,axis=1)*B[:,O[t1]]
        b_t = np.sum(A*B[:, O[-t1]]*b_t, axis = 1)
        a_t_his.append(a_t)
        b_t_his = [b_t] + b_t_his
    
    return [np.argmax(b_t_his[i]*a_t_his[i]) for i in range(t)]

optimized_path(O, A, B, pi)

# 输出：[2, 1, 2, 1, 1]

ref：

[1]李航. 统计学习方法[M]. 清华大学出版社, 2012.