Java集合详解--什么是Map

引言

---

在很久很久以前，讲过Set的实现原理，讲到Set就是Map的马甲，那么今天我们就来看看Map是如何实现的（本文都基于JDK1.8的版本）

什么是Map

---

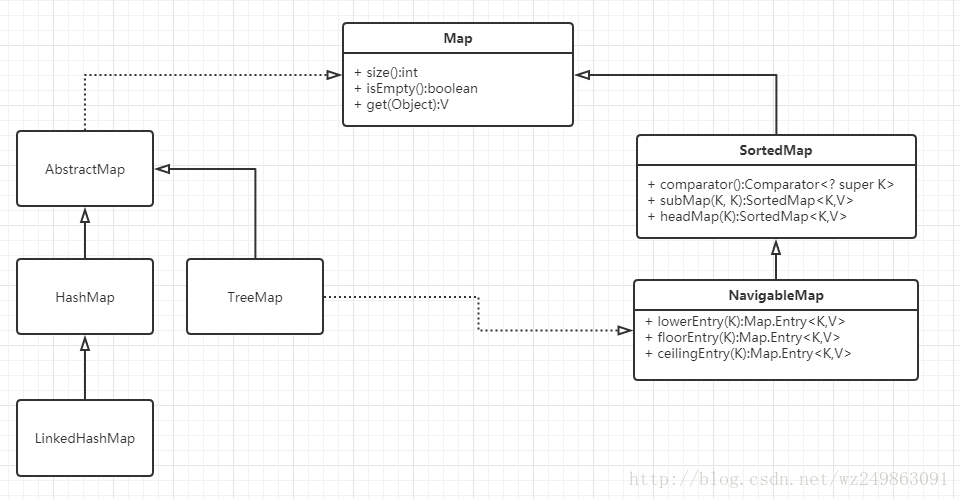
Map和Collection有关的几个map的关系图

• Map的定义

java.util
public interface Map<K, V>
An object that maps keys to values. A map cannot contain duplicate keys; each key can map to at most one value.
This interface takes the place of the Dictionary class, which was a totally abstract class rather than an interface.
The Map interface provides three collection views, which allow a map's contents to be viewed as a set of keys, collection of values, or set of key-value mappings. The order of a map is defined as the order in which the iterators on the map's collection views return their elements. Some map implementations, like the TreeMap class, make specific guarantees as to their order; others, like the HashMap class, do not.

• Map的三个特点

  1.包含键值对
  2.键唯一
  3.键对应的值唯一

Map还提供了3个集合视图，分别是一组键值对，一组键，一组值

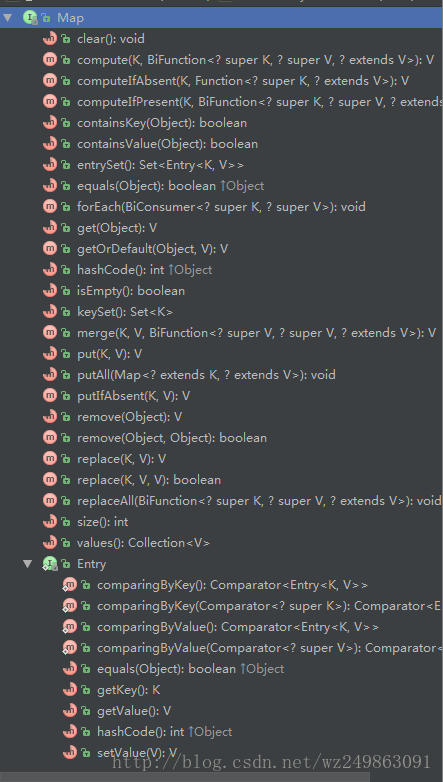
• Map有哪些方法
  
  
  

源码分析

---

• HashMap

  先来看看常量

/**
 * The default initial capacity - MUST be a power of two.
 */
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

/**
 * The maximum capacity, used if a higher value is implicitly specified
 * by either of the constructors with arguments.
 * MUST be a power of two <= 1<<30.
 */
static final int MAXIMUM_CAPACITY = 1 << 30;

/**
 * The load factor used when none specified in constructor.
 */
static final float DEFAULT_LOAD_FACTOR = 0.75f;

/**
 * The bin count threshold for using a tree rather than list for a
 * bin.  Bins are converted to trees when adding an element to a
 * bin with at least this many nodes. The value must be greater
 * than 2 and should be at least 8 to mesh with assumptions in
 * tree removal about conversion back to plain bins upon
 * shrinkage.
 */
static final int TREEIFY_THRESHOLD = 8;

/**
 * The bin count threshold for untreeifying a (split) bin during a
 * resize operation. Should be less than TREEIFY_THRESHOLD, and at
 * most 6 to mesh with shrinkage detection under removal.
 */
static final int UNTREEIFY_THRESHOLD = 6;

/**
 * The smallest table capacity for which bins may be treeified.
 * (Otherwise the table is resized if too many nodes in a bin.)
 * Should be at least 4 * TREEIFY_THRESHOLD to avoid conflicts
 * between resizing and treeification thresholds.
 */
static final int MIN_TREEIFY_CAPACITY = 64;

如果不指定初值的话，列表的长度就为16，默认加载因子为0.75，

再来看看成员变量

/**
 * The table, initialized on first use, and resized as
 * necessary. When allocated, length is always a power of two.
 * (We also tolerate length zero in some operations to allow
 * bootstrapping mechanics that are currently not needed.)
 */
transient Node<K,V>[] table;
这个就是列表

/**
 * Holds cached entrySet(). Note that AbstractMap fields are used
 * for keySet() and values().
 */
transient Set<Map.Entry<K,V>> entrySet;
这个是用于缓存节点

/**
 * The number of key-value mappings contained in this map.
 */
transient int size;
已经用于的节点数量

/**
 * The number of times this HashMap has been structurally modified
 * Structural modifications are those that change the number of mappings in
 * the HashMap or otherwise modify its internal structure (e.g.,
 * rehash).  This field is used to make iterators on Collection-views of
 * the HashMap fail-fast.  (See ConcurrentModificationException).
 */
transient int modCount;
这个是修改的次数

/**
 * The next size value at which to resize (capacity * load factor).
 *
 * @serial
 */
// (The javadoc description is true upon serialization.
// Additionally, if the table array has not been allocated, this
// field holds the initial array capacity, or zero signifying
// DEFAULT_INITIAL_CAPACITY.)
int threshold;
极限值，如果节点数大于这个值就需要扩容了，这个值的计算方式是capacity * load factor

/**
 * The load factor for the hash table.
 *
 * @serial
 */
final float loadFactor;
加载因子，决定了节点数值大于当前总数的一定百分比时，扩容

接下来的是构造函数

public HashMap(int initialCapacity, float loadFactor) {
    if (initialCapacity < 0)
        throw new IllegalArgumentException("Illegal initial capacity: " +
                                           initialCapacity);
    if (initialCapacity > MAXIMUM_CAPACITY)
        initialCapacity = MAXIMUM_CAPACITY;
    if (loadFactor <= 0 || Float.isNaN(loadFactor))
        throw new IllegalArgumentException("Illegal load factor: " +
                                           loadFactor);
    this.loadFactor = loadFactor;
    this.threshold = tableSizeFor(initialCapacity);
}

public HashMap(int initialCapacity) {
    this(initialCapacity, DEFAULT_LOAD_FACTOR);
}

public HashMap() {
    this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}

如果了解当前数据的量的话，建议规定HashMap的大小，减少扩容次数，提高性能

public HashMap(Map<? extends K, ? extends V> m) {
    this.loadFactor = DEFAULT_LOAD_FACTOR;
    putMapEntries(m, false);
}
这个是从已有的Map中生成一个新的Map，属于深拷贝

接下来看下get的实现

public V get(Object key) {
    Node<K,V> e;
    return (e = getNode(hash(key), key)) == null ? null : e.value;
}

final Node<K,V> getNode(int hash, Object key) {
    Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
//首先看看列表是否为空
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (first = tab[(n - 1) & hash]) != null) {
//不为空的话，碰碰运气，检查下第一个是不是我们要找到的
//判断条件是hash值一致，并且key一致
        if (first.hash == hash && // always check first node
            ((k = first.key) == key || (key != null && key.equals(k))))
            return first;
        if ((e = first.next) != null) {
            if (first instanceof TreeNode)
                return ((TreeNode<K,V>)first).getTreeNode(hash, key);
            do {
//根据下面介绍的哈希冲突解决方法，了解到每个数据项都是一个链表，因此需要遍历这个链表去找到我们需要的key那项
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            }