大话系列 | 逻辑回归的入门与优化

↑关注+星标，听说他有点东西

全文共2307字，阅读全文需8分钟

写在前面的的话

大家好，我是小一

这是大话系列的第8节算法，也是本系列的第16篇原创文章。

阅读本文请先了解线性回归的算法推导与优化：大话系列 | 线性回归的推导与优化

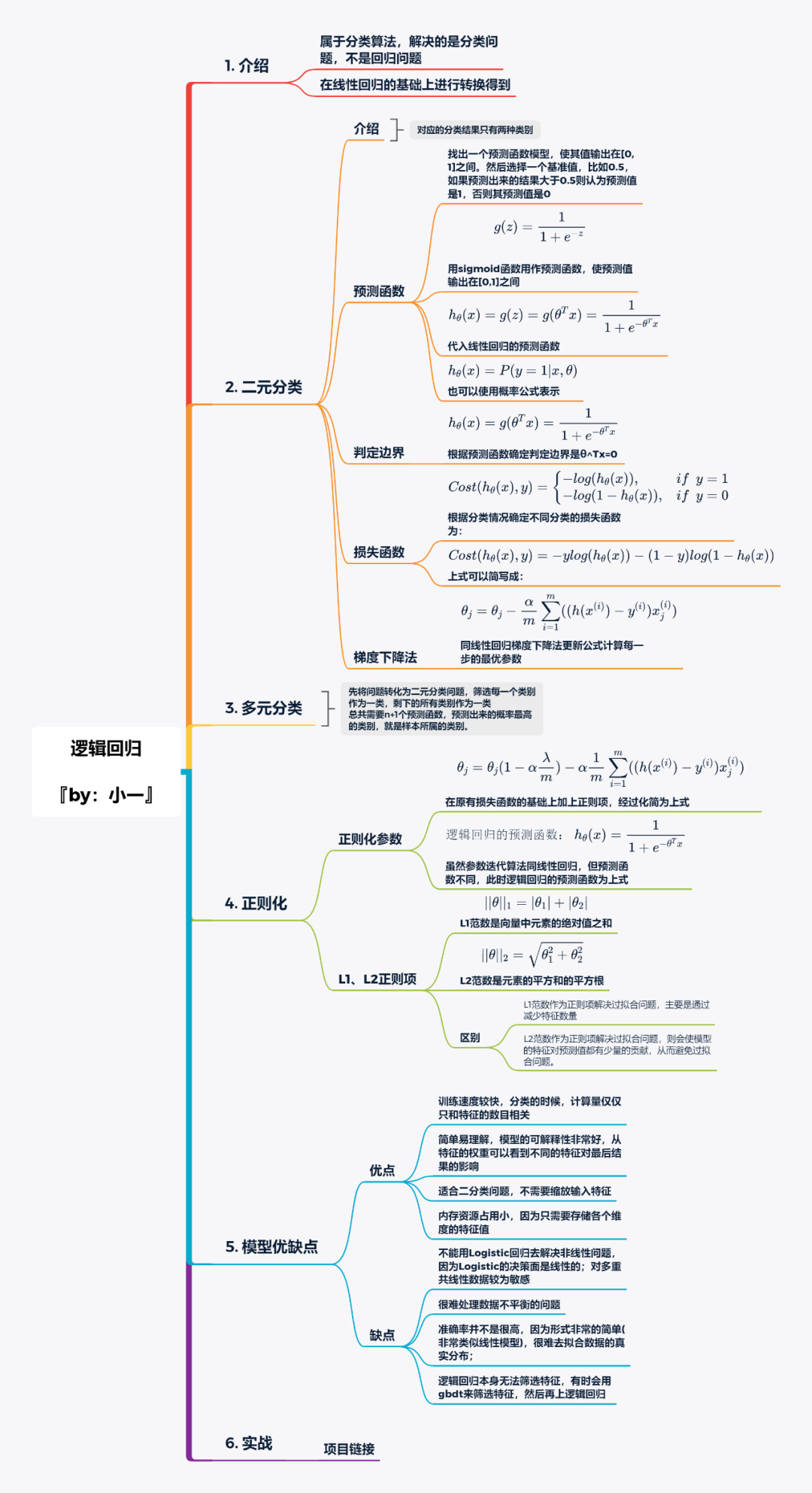
文末附逻辑回归的思维导图。

逻辑回归

了解逻辑回归之前，需要先明确一点：逻辑回归解决的是分类问题。那么既然是解决分类问题，前面也提到了六篇分类算法，为什么没有写在一起呢？

首先因为它是基于线性回归的基础，其次是在线性回归的基础进行一个转换就可以得到。

和前面的部分分类算法一样，逻辑回归同样支持二元分类和多元分类。

二元分类逻辑回归

介绍

只要算法的输出是一个分类变量那么这个算法就是一个分类算法，如果输出的结果只有两种分类结果，那么此时的分类算法就是二元分类算法。

比如说一场球赛最终的输（用0表示）赢（用1表示），病人肿瘤的预测结果是恶性（用0表示）还是良性（用1表示）等等这些都是二元分类问题。

预测函数

在二元分类中，需要找出一个预测函数模型，使其值输出在[0,1]之间。然后选择一个基准值，比如0.5，如果预测出来的结果大于0.5则认为预测值是1，否则其预测值是0。这个时候，可以用sigmoid函数用作预测函数：

sigmoid 函数又称为Logistic 函数，以z为横坐标，以g(z)为纵坐标，则sigmoid函数的图形如下：

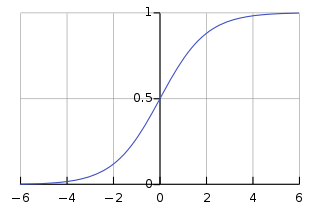
从图中可以看出，当z=0时，g(z)=0.5；当z>0时，g(z)>0.5，当z越来越大时，g(z)无限接近于1；当z<0时，g(z)<0.5，当z越来越小时，g(z)无限接近于0。

sigmoid函数的这个性质正和我们想要的预测函数是一样的性质，所以为了将输入特征和预测函数结合起来，我们可以将线性回归的预测函数带入到逻辑回归的预测函数中。

上一节我们知道线性回归的预测函数，假设另，则逻辑回归的预测函数可以写成：

此时的表示在输入值为x，参数为θ的前提条件下y=1的概率，如果用概率论的公式也可以写成：

此时的这个是一个条件概率公式，因为对于二元分类来说，不是黑就是白，所以黑白相加的和是1

判定边界

在逻辑回归中，有一个很重要的一点：判定边界。

我们知道sigmoid函数是把0.5作为判定边界，大于0.5的判定为结果1，小于0.5的判定为结果0。这个是针对g(z)进行判定的结果，但是在上一节我们已经把z用线性回归的预测函数代替：

所以根据y=1的判定条件，y=0的判定条件，可以推导出y=1的判定条件是，y=0的判定条件是。

所以，是我们最终的判定边界

损失函数

对于分类问题的损失函数，我们可以通过计算被分类错误的样本的比例，再细分一下，我们可以分别考虑y=1和y=0两种情况下预测值与真实值的误差，通过计算每个样本的误差最终计算整体样本点的损失情况。

此时，我们的损失函数可以写成：

如果 θ，那么损失为 ；如果 θ，那么成本将是无穷大 。

如果 θ，那么成本为 ；如果 θ，那么成本将是无穷大

基于上面的分析，最终的损失函数可以统一写成：

因为是离散值，当y=1时，1-y=0，上面公式的后半部分是0；当y=0时，上面公式的前半部分是0。

所以上面公式和分开表达的计算公式是等价的。

梯度下降法

和线性回归算法类似，在计算损失函数最优参数的时候同样可以使用梯度下降法

根据梯度下降公式：

我们可以确定θ的更新过程：

其中，α是学习率（也就是每一步的步长），m是训练样本的个数，针对上面这个公式，我们可以在每一步去更新θ的值。

多元分类逻辑回归

使用逻辑回归解决多元分类问题时，可以先将问题转化为二元分类问题。

例如针对多元分类 ，总共有n+1个类别，此时将y=0看做一个类别， 作为另一个类别，分别计算这两个类别的概率。

接着，把y=1作为一个类别，把 作为另外一个类别，在计算这两个类别的概率。

由此推广开，总共需要n+1个预测函数，预测出来的概率最高的类别，就是样本所属的类别。

正则化

逻辑回归的正则化

和线性回归同样的思路，我们可以对逻辑回归的损失函数进行正则化，方法也是在原有损失函数的基础上加上正则项：

相应的，正则化后的参数迭代公式为：

逻辑回归的参数迭代算法和线性回归是一样的，但是它们的算法不一样，因为两个式子的预测函数不一样，线性回归的预测函数，而逻辑回归的预测函数

L1、L2正则项

在创建逻辑回归模型时，有一个参数penalty，取值有'l1'或者'l2'，对应正则项参数L1范数和L2范数。

L1范数和L2范数都是针对向量的一种运算。假设模型只有两个参数，它们构成一个二维向量，此时L1范数、L2范数分别为：

即L1范数是向量中元素的绝对值之和，L2范数是元素的平方和的平方根

因为L1范数作为正则项，会让模型参数θ稀疏化，也就是让模型参数向量里为0的元素尽量多；而L2范数作为正则项，则是让模型参数尽量小，但不会为0，也就是尽量让每个特征对预测值都有一些小的贡献。

所以，L1范数作为正则项解决过拟合问题，主要是通过减少特征数量；L2范数作为正则项解决过拟合问题，则会使模型的特征对预测值都有少量的贡献，从而避免过拟合问题。

模型优缺点

优点

• 训练速度较快，分类的时候，计算量仅仅只和特征的数目相关；

• 简单易理解，模型的可解释性非常好，从特征的权重可以看到不同的特征对最后结果的影响；

• 适合二分类问题，不需要缩放输入特征；

• 内存资源占用小，因为只需要存储各个维度的特征值；

缺点

• 不能用Logistic回归去解决非线性问题，因为Logistic的决策面是线性的；对多重共线性数据较为敏感；

• 很难处理数据不平衡的问题；

• 准确率并不是很高，因为形式非常的简单(非常类似线性模型)，很难去拟合数据的真实分布；

• 逻辑回归本身无法筛选特征，有时会用gbdt来筛选特征，然后再上逻辑回归

思维导图

写在后面的话

还是老规矩，加小一微信领取高清思维导图，或者每次推文后都会在交流群内分享，需要的自己保存。

更多算法请点击文章开头的专辑