2021年美赛F题总结
肝到了早上六点20分才算是把F题的论文交上去了呜呜,最后把论文发给官方的时候3个人紧张死了,检查了7,8遍就怕出一点错,官方不接收我们的文章,那个点已经神志不清了,又在官网不停刷新,终于看到receive才安心的去睡觉了,一觉起来下午3点了,哈哈哈哈,太能睡了。
不好意思 在备考研究生了很少看CSDN了,这下面几个网站是我培训时用过与学习过的,上面拥有完整的代码和解释还有历年论文,非常齐全。
1、matlab代码
matlab算法代码及解析
2、python代码
3、按模型整理的美赛论文
4、我整理的数据(19年)(PS:部分数据存在出入)

文章目录
F题 题目翻译
问题F:检查高等教育的脉搏和温度
一个国家拥有一个健康、可持续的高等教育系统意味着什么? 什么问题重要?它是成本、机会、公平、资金、学位的价值、教育质量、研究水平、世界上最聪明的头脑的思想交流、上述的一些、所有的,还是其他的东西?高等教育制度是一个国家努力进一步教育其公民而不是所需的初等和中等教育的一个重要因素,因此,它既是一个行业本身,也是国家经济受过培训和教育的公民的来源。当我们环顾世界,从德国到美国,从日本到澳大利亚,我们看到各种国家的高等教育方法,这些国家不仅教育自己的学生,而且每年吸引大量的国际学生。这些国家的高等教育体系各有其长处和短处,在当前大流行病所需要的调整之后,各国有机会思考什么是可行的,什么是更好的。然而,改变往往是困难的。推进任何制度所需的体制改革都需要长期执行政策,以便建立一个更加健康和可持续的制度。在这个问题上,你将开发一个模型来衡量和评估国家一级高等教育系统的健康状况,以确定一个健康和可持续的状态考虑到国家的高等教育制度,并提出和分析一套政策,将一个国家从目前的状态迁移到你提议的健康和可持续的状态。具体来说,你被要求:
-
开发和验证一个模型或一套模型,使您能够评估任何国家的高等教育系统的健康状况;
-
将您的模型应用于几个国家,然后根据您的分析,选择一个其高等教育系统有改进空间的国家;
-
为你选定的国家的制度提出一个可实现和合理的愿景,以支持一个健康和可持续的高等教育系统;
-
使用您的模型来衡量当前系统的健康状况,以及为您选定的国家提出的、健康的、可持续的系统;
-
提出有针对性的政策和实施时间表,以支持从当前状态迁移到您提议的状态;
-
使用您的模型来塑造和/或评估您的政策的有效性;
-
讨论在过渡期间和最终状态下实施你的计划对现实世界的影响(例如对学生、教师、学校、社区、国家),承认改变是困难的现实。
提示:以下是本篇文章正文内容,下面案例可供参考
一、敲定选题
这次美赛的题目都好难,根据同学选B题的同学来说,火山经纬度、海拔什么的数据基本找不到。我们在美赛开始之前本来想做了C题,赛前也做了C题的演练,但是嘛,今年的C题不说了,美赛yyds!600M的图片集和视频集,正负样本差异化太大了,因为不会深度学习算法,用感知哈希算法跑了一波,直接GG,识别不出那个亚洲大黄蜂和其他蜜蜂什么的区别,然后老师也说图像处理这方面也非常困难(包括背景不一致,关键位置提取困难)然后我们就放弃了这个 倒萨货(方言);我们的老师本来推荐我们选D题,因为这道题目和2020C题很像,但是我第一题画了个图就直接蒙B了,然后题目也没啥灵感,晚上查查好像ICM的获奖率挺高的,就选了F题,主要第一次参加很紧张,然后实力不够,就选了F题。
用Gephi画的G题第一题,一团乌漆嘛黑
二、题目解析
1、数据搜集
首先F题的数据要自己找的,而且这道题要用到很多的国家的权威数据,建议大家可以使用谷歌浏览器+谷歌浏览助手这样子就可以访问外网了,然后我们的数据主要来自各个国家的数据库和联合国教科文组织、世界银行这些权威的数据组织。
下面这几个网站就是我们查数据用到的:
2、数据处理
1、拉格朗日插值法处理缺失数据
因为搜集到的数据存在缺失(很多国家的最新数据都是无的),然后这里就需要用到数据填充来弥补缺失的数据。
我们用的方法是拉格朗日插值法,画出来的图大概是这样的(代码是根根据其他博主改编的,但是一下没招待地址,后续会加上去)

代码如下(示例):
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.interpolate import lagrange
def polyinterp(data, k=5):
df1 = data.copy()
print("原始数据(含缺失值):", '\n', data)
for i in range(len(df1)):
if (df1['rate of employment'].isnull())[i]:
# 取数索引范围,向插值前取k个,向后取k个
index_ = list(range(i - k, i)) + list(range(i + 1, i + 1 + k)) # Series索引不为负数
list0 = [j for j in index_ if j in df1['rate of employment'].sort_index()]
y = df1['rate of employment'][list0]
y = y[y.notnull()] # 索引为负则为缺失值,去掉缺失值
f = lagrange(y.index, list(y))
df1.iloc[i, 1] = f(i)
# print("副本插值后:",'\n',df1)
print("副本插值后:", '\n', df1[40:])
return (df1)
def chart_view(df01, df1):
df1.rename(columns={'rate of employment': 'New rate of employment'}, inplace=True)
df01['rate of employment'].plot(style='k--')
df1['New rate of employment'].plot(alpha=0.5)
plt.legend(loc='best')
plt.show()
if __name__ == '__main__':
df01 = pd.read_csv(r'large1.csv', encoding='UTF-8')
df1 = df01.copy()
new_data = polyinterp(df1, 5) # 插值后
chart_view(df01, new_data) # 插值前后绘图
稍微修改以下数据就能运行
2、Max-Min标准化处理数据
为了降低指标处理的难度,我们对数据进行归一化操作,把数据映射到0~1范围之内处理。
我们采取最大-最小归一化的方法,公式如下:
x
i
j
=
x
i
j
−
min
{
x
1
j
,
x
2
j
,
.
.
.
,
x
n
j
}
max
{
x
1
j
,
x
2
j
,
.
.
.
,
x
n
j
}
−
min
{
x
1
j
,
x
2
j
,
.
.
.
,
x
n
j
}
{{\rm{x}}_{ij}}{\rm{ = }}\frac{{{x_{ij}} - \min \{ {x_{1j}},{x_{2j}},...,{x_{nj}}\} }}{{\max \{ {x_{1j}},{x_{2j}},...,{x_{nj}}\} - \min \{ {x_{1j}},{x_{2j}},...,{x_{nj}}\} }}
xij=max{x1j,x2j,...,xnj}−min{x1j,x2j,...,xnj}xij−min{x1j,x2j,...,xnj}
2、问题一
建立CIPP评价模型
这一问要求我们建立一个高等教育评价模型,我们根据CIPP模型,通过建立“基础 - 投入 - 过程 - 绩效”分析框架,确立了13评价个指标。
根据我们搜素到的的13个数据指标,我们对数据进行一定的预处理。同时,在对高等教育占GDP比重、毕业率、就业率等重要指标定性描述的基础上,建立高等教育评价系统,定性定量探究影响这些指标的重要因素,以及这些指标之间的内在联系。
然后下面是我们画的一些草图


3、问题二
1、基于熵权法的Topsis的评价模型
第一步:根据之前标准化的结果求解熵权熵值
E
j
=
−
1
ln
n
∑
i
=
1
n
p
i
j
ln
(
p
i
j
)
(
j
=
1
,
2
,
3
,
.
.
.
,
m
)
{E_j} = - \frac{1}{{\ln n}}\sum\limits_{i = 1}^n {{p_{ij}}\ln ({p_{ij}})(j = 1,2,3,...,m)}
Ej=−lnn1i=1∑npijln(pij)(j=1,2,3,...,m)
第二步:求解熵权
w
j
=
d
j
∑
j
=
1
n
d
j
(
j
=
1
,
2
,
3
,
.
.
.
,
m
)
{w_j} = \frac{{{d_j}}}{{\sum\limits_{j = 1}^n {{d_j}} }}(j = 1,2,3,...,m)
wj=j=1∑ndjdj(j=1,2,3,...,m)
第三步:确定正负理想解。
D
i
+
=
∑
j
=
1
m
(
V
i
j
+
−
V
j
+
)
2
(
i
=
1
,
2
,
.
.
.
,
m
)
D_{\rm{i}}^ + = \sqrt {\sum\limits_{j = 1}^m {{{(V_{ij}^ + - V_{\rm{j}}^ + )}^2}} } (i = 1,2,...,m)
Di+=j=1∑m(Vij+−Vj+)2(i=1,2,...,m)
D
i
−
=
∑
j
=
1
m
(
V
i
j
+
−
V
j
−
)
2
(
i
=
1
,
2
,
.
.
.
,
m
)
D_{\rm{i}}^ - = \sqrt {\sum\limits_{j = 1}^m {{{(V_{ij}^ + - V_{\rm{j}}^ - )}^2}} } (i = 1,2,...,m)
Di−=j=1∑m(Vij+−Vj−)2(i=1,2,...,m)
第四步:得出方案最优评分
T
=
D
−
D
+
+
D
−
T = \frac{{{D^ - }}}{{{D^ + } + {D^ - }}}
T=D++D−D−
然后根据算出的评分,GER、GBR、USA这三个国家的排名前三,并且确定了GDP、顶尖学校占比(前1000名)这两个关键指标。
2、因子分析证明
通过因子分析,同样也确定了GDP、顶尖学校占比(前1000名)这两个关键指标,并且他们的贡献率分别为0.966和0.968。证明了我们模型的适用性。
问题三
提了一点建议
对印度高等教育体系发展的建议
和其他国家的平均水平横向分析了一波印度的缺陷,然后提点意见

·加快国家经济发展,提高人均国内生产总值。
·加大教育投入力度,提高学校办学质量,发展顶尖院校
·加大教育扶持力度,提高高等教育入学率
·增加师资力量,广招人才
问题四
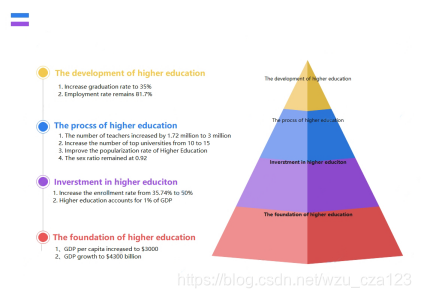
题目要求我们规划一下我们选择的国家的执行时间表
然后我就按找金字塔形结合之前的CIPP模型画了一个图
问题五
时间序列滑动平均模型
因为变量、因变量与各自变量的“过去”和“现在”都可能存在统计依赖关系。所以,我们采取了基于时间序列滑动平均模型对印度未来五年数据进行预测.
问题六
对比印度在不同状态下的未来5年高等教育体系发展状况,基于基于上述数据运用时间序列滑动平均模型计算出来的结果,我们重新计算印度高等教育体系的评分,结果如下图所示:
一个是按照印度自身发展预测的,一个是按照我们制定的计划预测的
印度排名变化还是明显的,证明我们的预测和计划还是可以的。


对比一下两张图
问题七
没看懂题目,水了一点建议
后续
三个人在最后一天肝了20个小时呜呜呜

睡醒已经是下午两点了,和朋友出去吃了个饭,然后就开始写这篇博客了,写的不是很清晰的感觉,毕竟我是一个小萌新哈哈哈
还有我的两位优秀的小伙伴,他们都太棒了,在做的过程中提了很多有用的建议,并且能够一起坚持到最后,太爱她们了,泪目!!!(博主是男的,狗头保命哈哈哈哈哈哈哈哈哈哈哈哈)
再谈谈我自己吧,2020年下半年诸事不顺,谈恋爱、学习什么的都挺失败的,还挺沉溺lol的,害,都是我自身的原因。希望2021年能够过的稍微好一点,就是万幸啦!
希望2021年大家继续努力!!!!牛年牛气冲天!!!!
想要数据的小伙伴@一下我,我过几天传上去。

























 3446
3446

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










