算法－最短路径

图的最短路径问题是一个经典的计算机科学和运筹学问题，旨在找到图中两个顶点之间的最短路径。这种问题在多种场景中都有应用，如网络路由、地图导航等。

解决图的最短路径问题有多种算法，其中最著名的包括：
1.迪杰斯特拉算法
(1). 图的要求
适用于权重非负的图。
(2). 实现
该算法的实现通常包括以下步骤：
a. 初始化：将源节点标记为最短路径已经知道．设置其路径距离为0．将其入队列．
b. 循环迭代，直到队列为空
b.1. 出队列，得p．
b.2.迭代&更新．
即对从p可达，且最短路径尚未确定节点q．
比较，若p的路径距离+Edge<p,q>小于q的路径距离，则更新q的路径距离=p的路径距离+Edge<p,q>．设置p为其路径上一节点．
b.3.从最短路径尚未确定节点中选出路径值最小节点t．将t的最短路径标记为已经知道．t入队列．在无法选出这样的t时，表示剩余节点均不可达．可提前结束迭代．

(3). 实例

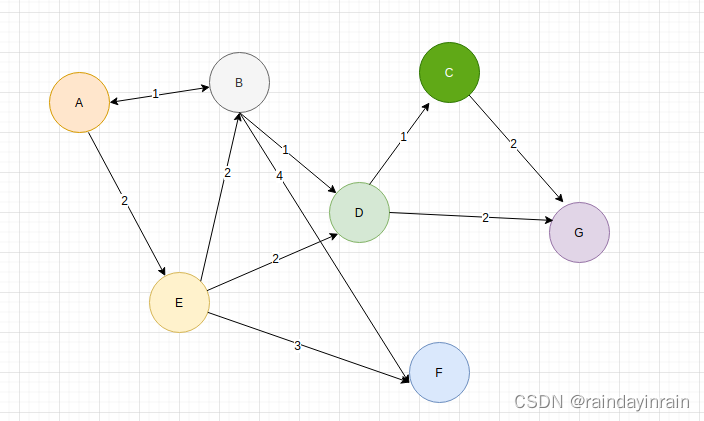
(4). 算法实现

#define MAX 0x7fffffff
class NodeInfo{
public:
    char m_nName;
    int32_t m_nPath = MAX;
    int32_t m_nPreIndex = -1;
    int32_t m_nTag = -1;
};

template<class T>
class Node{
public:
    T m_nEle;
};

template<class EdgeInfo>
class Edge{
public:
    int32_t m_nWeight = MAX;
    bool m_bValid = false;
};

Node<NodeInfo> stNodes[7];
Edge<int> stEdges[7][7];
void Sort(void* lpBegin, void *lpEnd);
int main(){
    stNodes[0].m_nEle.m_nName = 'A';
    stNodes[1].m_nEle.m_nName = 'B';
    stNodes[2].m_nEle.m_nName = 'C';
    stNodes[3].m_nEle.m_nName = 'D';
    stNodes[4].m_nEle.m_nName = 'E';
    stNodes[5].m_nEle.m_nName = 'F';
    stNodes[6].m_nEle.m_nName = 'G';
    
    stEdges[0][1].m_nWeight = 1;
    stEdges[0][1].m_bValid = true;
    stEdges[1][0].m_bValid = true;
    stEdges[1][0].m_nWeight = 1;

    stEdges[0][4].m_bValid = true;
    stEdges[0][4].m_nWeight = 2;

    stEdges[4][1].m_bValid = true;
    stEdges[4][1].m_nWeight = 2;

    stEdges[1][3].m_bValid = true;
    stEdges[1][3].m_nWeight = 1;

    stEdges[1][5].m_bValid = true;
    stEdges[1][5].m_nWeight = 4;
    stEdges[4][3].m_bValid = true;
    stEdges[4][3].m_nWeight = 2;
    stEdges[3][2].m_bValid = true;
    stEdges[3][2].m_nWeight = 1;
    stEdges[3][6].m_bValid = true;
    stEdges[3][6].m_nWeight = 2;
    stEdges[2][6].m_bValid = true;
    stEdges[2][6].m_nWeight = 2;
    
    int nSourceIndex = 0;
    stNodes[nSourceIndex].m_nEle.m_nTag = 1;
    stNodes[nSourceIndex].m_nEle.m_nPath = 0;
    stNodes[nSourceIndex].m_nEle.m_nPreIndex = -1;

    int32_t nArrQueue[7];
    int32_t nFirst = 0;
    int32_t nEnd = 0;
    int32_t nNum = 0;
    nArrQueue[0] = nSourceIndex;
    nFirst = 0;
    nEnd = 1;
    nNum = 1;
    while(nNum > 0){
        // 出队列
        int32_t nIndex;
        if(nNum = 1){
            nIndex = nArrQueue[nFirst];
            nFirst = 0;
            nEnd = 0;
            nNum = 0;
        }
        else{
            nIndex = nArrQueue[nFirst];
            nFirst = (nFirst+1)%7;
            nNum--;
        }

        // 迭代&更新
        for(int32_t i = 0; i < 7; i++){
            if(stEdges[nIndex][i].m_bValid && stNodes[i].m_nEle.m_nTag == -1){
                if(stNodes[i].m_nEle.m_nPath > stNodes[nIndex].m_nEle.m_nPath + stEdges[nIndex][i].m_nWeight){
                    stNodes[i].m_nEle.m_nPath = stNodes[nIndex].m_nEle.m_nPath + stEdges[nIndex][i].m_nWeight;
                    stNodes[i].m_nEle.m_nPreIndex = nIndex;
                }
            }
        }

        // 入队列
        // 选择未访问节点中最短距离最小的一个
        nIndex = -1;
        int32_t nMin = MAX;
        for(int32_t i = 0; i < 7; i++){
            if(stNodes[i].m_nEle.m_nTag == -1 && stNodes[i].m_nEle.m_nPath < nMin){
                nMin = stNodes[i].m_nEle.m_nPath;
                nIndex = i;
            }
        }
        if(nIndex == -1){
            break;// 所有节点均已被访问．或剩余节点全部不可达．
        }
        // 选举的节点就是最短路径已知的
        stNodes[nIndex].m_nEle.m_nTag = 1;
        if(nNum == 0){
            nArrQueue[0] = nIndex;
            nFirst = 0;
            nEnd = 1;
            nNum++;
        }
        else{
            nArrQueue[nEnd] = nIndex;
            nEnd = (nEnd+1)%7;
            nNum++;
        }
    }

    // test
    printf("finish\n");
    while(true){
        int32_t nIndex = -1;
        scanf("%d", &nIndex);
        getchar();
        printf("path_%d\n", stNodes[nIndex].m_nEle.m_nPath);
        printf("%c ", stNodes[nIndex].m_nEle.m_nName);
        while(nIndex != -1){
            printf("%c ", stNodes[stNodes[nIndex].m_nEle.m_nPreIndex].m_nEle.m_nName);
            nIndex = stNodes[nIndex].m_nEle.m_nPreIndex;
        }
        printf("\n");
    }
    return 0;
}

2.贝尔曼-福特算法（Bellman-Ford Algorithm）：
(1). 图的要求
可以处理带有负权重的图，但无法处理包含负权重环的图。
针对权重为负的图，可以让所有边权中加上一个基础量转变为权重非负的，再通过迪杰斯特拉求解．所以，正常没必要用这个．
时间复杂度为O(|V|*|E|)。

(2). 算法
贝尔曼-福特算法（Bellman-Ford Algorithm）的实现过程可以分为以下三个阶段：

a. 初始化阶段：
创建一个数组Distant，用于记录从源点s到图中各个顶点的最短路径长度估计值。通常，将源点s到自己的距离Distant[s]初始化为0，而将源点s到其他所有顶点的距离初始化为一个较大的值（如无穷大），表示这些顶点与源点之间的最短路径尚未确定。
b. 松弛操作阶段：
这个阶段需要进行|V|-1次迭代，其中V是图中顶点的数量。在每一次迭代中，遍历图中的所有边(u, v)，并检查是否可以通过这条边来更新从源点s到顶点v的最短路径长度估计值。
具体来说，对于每一条边(u, v)，如果Distant[u] + w(u, v) < Distant[v]，则更新Distant[v]为Distant[u] + w(u, v)。这里，w(u, v)是边(u, v)的权重，表示从顶点u到顶点v的距离或成本。
通过不断的松弛操作，Distant数组中的值会逐渐逼近从源点到各个顶点的实际最短路径长度。
c. 负权回路检测阶段：
在完成|V|-1次松弛操作后，再进行一次额外的松弛操作。这次操作的目的是为了检测图中是否存在负权回路（即从某个顶点出发，经过一系列边后回到该顶点，且整个回路的总权重为负）。
如果在额外的松弛操作中，仍然有Distant数组的值被更新，那么就说明图中存在负权回路。因为负权回路的存在会导致最短路径问题无解，因为可以通过不断绕行负权回路来减小路径长度。
如果额外的松弛操作没有更新Distant数组的值，那么算法结束，Distant数组中存储的就是从源点到各个顶点的最短路径长度。