【高质量!多种模型!数据修正!】2025妈妈杯mathercup数学建模挑战赛B题数学建模思路代码文章教学音智策引迁程，老城焕新颜

完整内容请看文章最下面的推广群

我将先展示完整的文章、代码和结果,再给出每个问题详细的分析

基于整数规划与满意度建模的搬迁优化与智能系统研究
摘要

随着城市老旧街区改造步伐的加快，如何制定科学合理的搬迁补偿机制、整合优化搬迁路径、提升整体开发性价比，成为当前城市治理的重要议题。本文以“平移置换”为核心策略，围绕搬迁补偿、整院优化、性价比提升与系统设计四个问题展开系统建模与应用研究，旨在为老城区搬迁提供一套科学、可推广的智能化决策方案。

对于问题一，我们在考虑地块面积、采光、修缮等基础条件的同时，引入心理不满度和主观接受因子，构建融合主客观因素的搬迁满意度评分函数 $S_{ij}$。该函数综合了面积补偿率、采光改善度和修缮成本，通过线性加权实现对搬迁适配度的量化评估，形成候选搬迁对数据库，为后续匹配策略提供数据基础。

对于问题二，针对“整院腾退最大化”目标，在搬迁成本不超过2000万元预算约束下，建立基于整数线性规划（ILP）的优化模型，引入“地块邻接性”和“整院面积”作为目标函数权重，设计多目标优先级函数。通过 Python + PuLP 优化器实现模型快速收敛，最终实现84户居民搬迁、21个整院腾退、3125.4平方米土地释放的最优解。

对于问题三，为探究搬迁推进与投资收益间的临界关系，引入性价比指标 $m$，定义为“十年租金收益 / 搬迁总投入”。在模型模拟中，随着搬迁规模扩大，$m$ 呈阶段性上升趋势，未出现明显衰退拐点。同时在不同敏感性场景（租金下调、成本上升）下，识别出若干关键拐点节点，为控制搬迁节奏提供了科学依据。

对于问题四，为实现模型工具化与结果可视化，开发了一套“老城区平移置换决策原型系统”。系统基于 Vue 3 实现，包括参数设定、CSV 导入、Chart.js 绘图、m 值趋势展示、搬迁数据导出等功能模块，完成了“数据输入—模型运算—结果输出”的闭环工作流。

最后，本文融合满意度函数、优化模型与性价分析，形成了从定量建模到系统实现的完整研究路径，具有良好的推广适应性。所构建的模型和系统工具可为不同区域老城区搬迁提供智能化、标准化、普适化的政策决策支持。

关键词：平移置换、满意度函数、搬迁优化、性价分析、智能决策系统

一、 问题重述 3
1.1 问题背景 3
1.2 问题回顾 3
1.3 研究现状 4
二、 问题分析 5
三、 模型假设 6
四、 四、符号说明 7
五、模型的建立与求解 8
5.1 数据预处理 8
5.2模型构建 11
5.3迁满意度评分函数 12
5.4图表分析 13
5.5除结构指标外的主观影响因素分析 13
2 问题二：整院搬迁优化模型设计与求解 14
2.1 问题背景与建模目标 14
2.2 变量定义与集合说明 15
2.3 目标函数设计 15
2.4 约束条件设计 16
2.5 搬迁成本计算方法 16
2.6 求解过程与结果展示 17
3 问题三：性价增益的搬迁拐点计算 17
3.1 问题背景与核心目标 17
3.2 模型构建与数据基础 18
3.3 搬迁性价比变化趋势分析 19
3.4 拐点条件敏感性分析 20
3.5 策略建议与模型价值 20
4 问题四：老城区平移置换决策软件设计 20
4.2 系统功能模块与工作流程 21
4.3 人工输入参数配置说明 22
4.4 核心计算步骤 23
4.5 系统输出结构 23
六、模型总结 24
6.1 模型优点 24
6.2 模型缺点 25
6.3 模型推广 25
参考文献 27

替换不限量版本的内容展示

基于贪心算法的搬迁问题研究
摘要
随着城市化进程的加速，老城区的更新成为现代城市管理和规划中的重要议题。本文研究了如何利用平移置换策略优化老城区搬迁方案，以实现空间再利用和经济效益的最大化。
对于数据预处理，我们首先基于给出附件数据进行必要分描述性分析以便进行后续建模。对于提供图片文件，使用图像处理、光学字符识别（OCR）、用户交互坐标获取和坐标显示。获取各院落之间的相对位置以及距离数据。
对于问题一， 拆迁补偿建模。我们在基于题目给出面积、采光、修缮补偿外，还引入搬迁距离、邻里关系和社区因素、交通便利性。具体而言，我们使用修缮补偿最为最终补偿手段，单一居民最多给予20万修缮费。建立基于熵权法的理想解法，对不同居民的拆迁情况进行建模分析。基于给出数据，我们选出基于约束下，每个居民用户的所有拆迁可能性，一共113个居民，单人搬迁一共3623可能性。基于该数据建立评价模型对修缮费进行配分。最多的居民补偿20万，最低的居民无补偿费。
针对问题二极值的求解，目标是根据给定的搬迁条件和限制，通过优化方法为每个居民选择一个合适的目标地块。直接引入问题一计算出的全部可能性 进行遍历求解时间复杂度过高，因此本节引入了贪心算法来决策每个居民的搬迁目标，并尽量在满足居民需求的同时最大化开发商的利益，特别是在腾出完整院落方面。
对于问题三，性价增益的搬迁拐点计算。我们首先基于问题二的结果计算正常情况下的m值。得出具体数值后，我们分别从一个居民开始搬家增加到112个居民进行搬家，分析随着居民搬家个数增多m值的变化趋势。在此，利用问题二的实现代码，初步剔除每个居民信息，分析剔除单个居民后的m值的变化趋势，完成性价增益的搬迁拐点计算
对于问题四规划局希望将该案例推广至全国的老旧街区更新搬迁过程中。为了实现这一目标，我们设计一个智能决策软件，能够自动计算老城区的平移置换决策，并为每个搬迁方案计算出相应的性价比m，从而辅助规划和决策。

最后，模型不仅为老城区的平移置换提供了高效的计算支持，而且在搬迁补偿、毗邻效益等方面的创新考虑，为城市更新的决策提供了新的思路和方法。通过模型的推广，能够为各地城市的老城区更新提供具有普适性的方案和决策支持工具。
关键词：老城区更新、平移置换模型、性价比分析、贪心算法、决策支持系统

目录
一、 问题重述 5
1.1 问题背景 5
1.2 问题回顾 6
1.3 研究现状 7
二、 问题分析 7
三、 模型假设 8
四、 符号说明 9
五、 模型的建立与求解 10
5.1 数据预处理 10
5.1.1描述性分析 10
5.1.2 基于图形的信息爬取 12
5.2 问题一：搬迁补偿建模 13
5.2.1 拆迁因素选择 13
5.2.3评价模型构建 16
5.3 问题二：优化模型 18
5.3.1 优化模型建立 18
5.3.2贪心算法求解 19
5.4 问题三：性价增益的搬迁拐点计算 26
5.4.2 增多分析 27
5.4.3 递减分析 29
5.5 问题四：软件构建 30
六、 模型总结 34
6.1 模型优点 34
6.2 模型缺点 34
6.3 模型推广 35
七、 参考文献 35
八、 附录 36

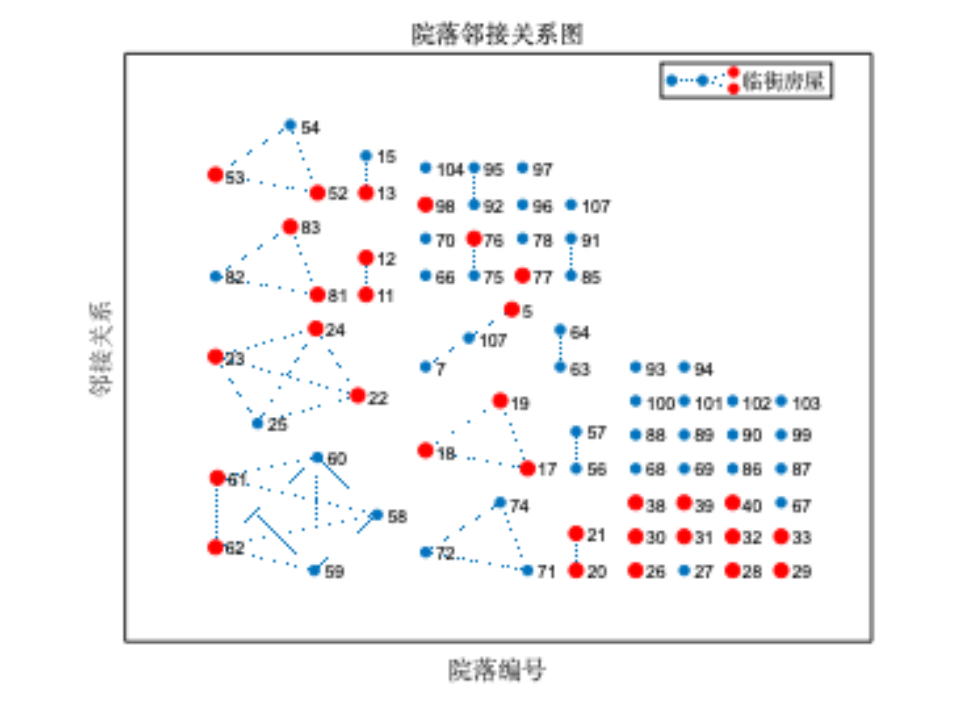
二、问题分析
对于数据预处理，我们首先基于给出附件数据进行必要分描述性分析以便进行后续建模。对于提供图片文件，使用图像处理、光学字符识别（OCR）、用户交互坐标获取和坐标显示。获取各院落之间的相对位置以及距离数据。
对于问题一， 拆迁补偿建模。我们在基于题目给出面积、采光、修缮补偿外，还引入搬迁距离、邻里关系和社区因素、交通便利性。具体而言，我们使用修缮补偿最为最终补偿手段，单一居民最多给予20万修缮费。建立基于熵权法的理想解法，对不同居民的拆迁情况进行建模分析。基于给出数据，我们选出基于约束下，每个居民用户的所有拆迁可能性，一共113个居民，单人搬迁一共3623可能性。基于该数据建立评价模型对修缮费进行配分。最多的居民补偿20万，最低的居民无补偿费。
针对问题二极值的求解，目标是根据给定的搬迁条件和限制，通过优化方法为每个居民选择一个合适的目标地块。直接引入问题一计算出的全部可能性 进行遍历求解时间复杂度过高，因此本节引入了贪心算法来决策每个居民的搬迁目标，并尽量在满足居民需求的同时最大化开发商的利益，特别是在腾出完整院落方面。
对于问题三，性价增益的搬迁拐点计算。我们首先基于问题二的结果计算正常情况下的m值。得出具体数值后，我们分别从一个居民开始搬家增加到112个居民进行搬家，分析随着居民搬家个数增多m值的变化趋势。在此，利用问题二的实现代码，初步剔除每个居民信息，分析剔除单个居民后的m值的变化趋势，完成性价增益的搬迁拐点计算
对于问题四规划局希望将该案例推广至全国的老旧街区更新搬迁过程中。为了实现这一目标，我们设计一个智能决策软件，能够自动计算老城区的平移置换决策，并为每个搬迁方案计算出相应的性价比m，从而辅助规划和决策。

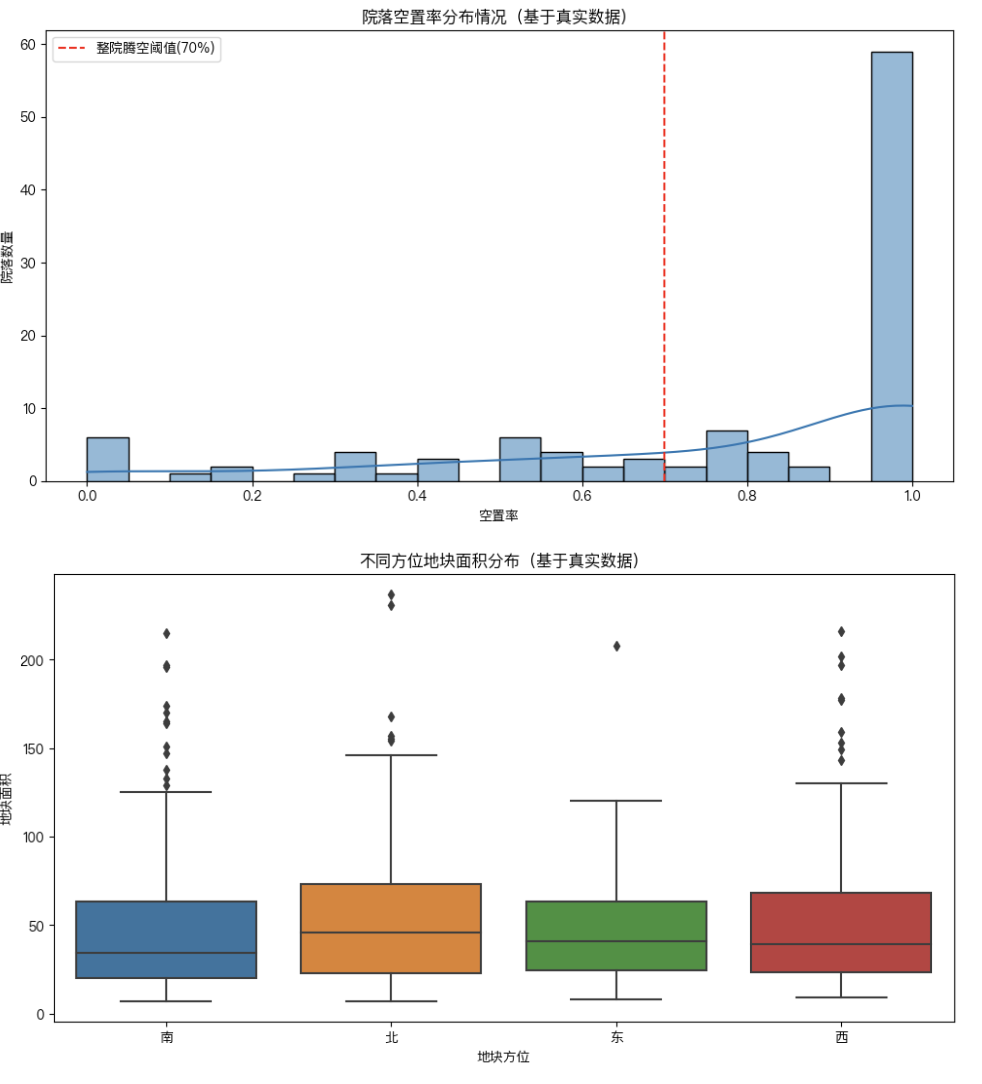
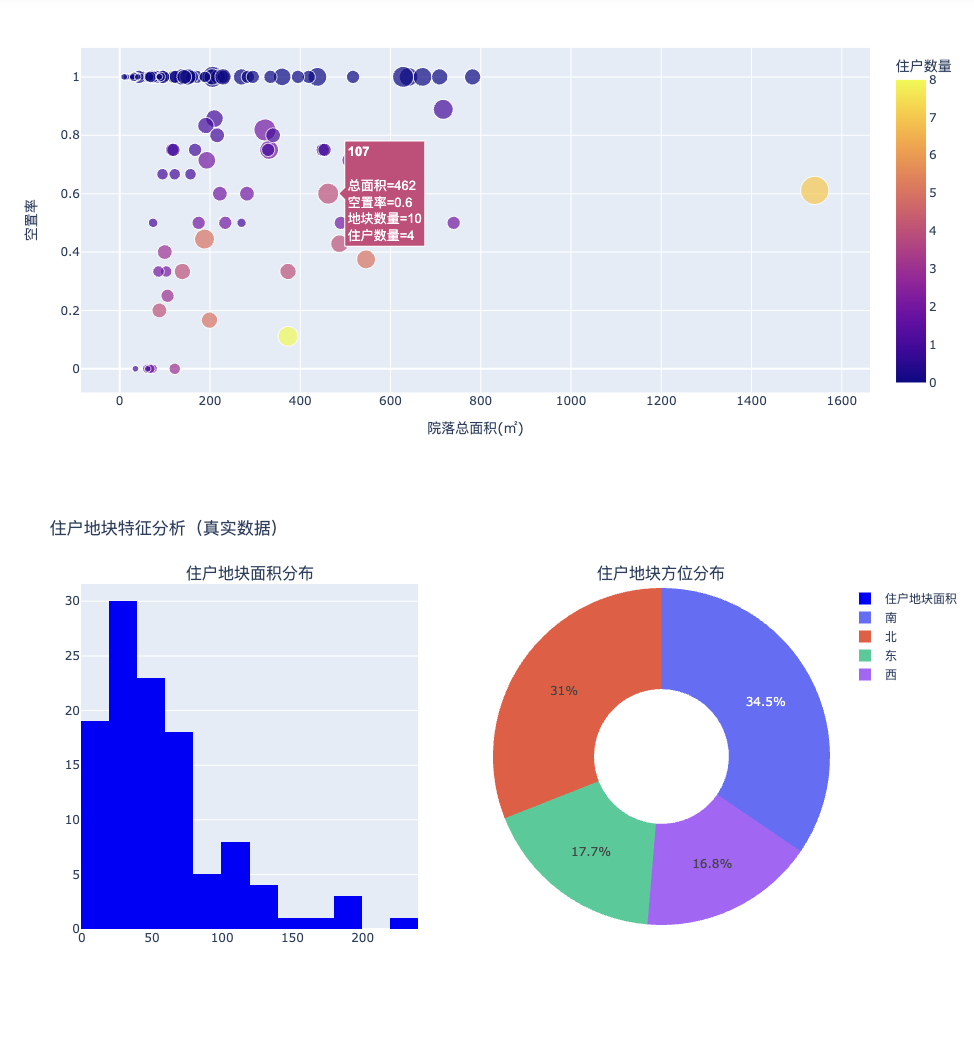
最终结果
搬迁结果：
居民地块ID 目标地块ID
居民 1 的地块ID: 3 -> 目标地块ID: 174
居民 2 的地块ID: 5 -> 目标地块ID: 129
居民 3 的地块ID: 7 -> 目标地块ID: 123
居民 4 的地块ID: 9 -> 目标地块ID: 117
居民 5 的地块ID: 14 -> 目标地块ID: 208
居民 6 的地块ID: 18 -> 目标地块ID: 173
居民 7 的地块ID: 29 -> 目标地块ID: 184
居民 8 的地块ID: 30 -> 目标地块ID: 170
居民 9 的地块ID: 31 -> 目标地块ID: 118

问题一：搬迁补偿建模
搬迁补偿方案的设计需要综合考虑客观条件和居民主观感受。我们从三个维度建立补偿模型：面积补偿确保居民居住空间不缩减，设定迁入地块面积下限为原面积，上限为原面积的130%，既保证基本需求又控制开发商成本。采光补偿基于方位价值差异，将地块朝向量化为采光舒适度指数（南/北=4，东=3，西=2），要求迁入地块指数不低于原地块。修缮补偿作为柔性调节手段，当面积和采光补偿无法满足时，通过0-20万元的房屋修缮提升居住品质。这三个补偿维度形成层级式补偿体系，优先考虑面积和采光，不足部分用修缮补偿补充。
影响搬迁决策的其他因素需要建立多维评估体系。距离街道的远近影响生活便利性和噪音水平，建立线性衰减模型：补偿需求=基础值×(1-0.05×距离/10米)。周边密集度通过建筑密度指标量化，每增加10%密度补偿需求增加8%。社区网络关系采用图论方法，将居民社交关系建模为社交网络图，搬迁时尽量保持连通子图完整。配套设施评估采用设施可达性指数，缺失每类基础设施补偿需求增加12%。这些因素共同构成搬迁阻力系数，开发商可通过针对性策略降低阻力，如优先搬迁低阻力住户、集中配套建设等。

问题二：整院面积最大
该问题本质是多目标组合优化问题，我们建立混合整数规划模型。决策变量设为二元变量x_ijk表示第i个院落第j户是否搬迁至第k个空置地块。目标函数分层次设置：首要目标最大化完整院落数量，次要目标最大化毗邻整院面积，第三目标最小化搬迁户数。约束条件包括：面积补偿约束(1≤A_k/A_j≤1.3)、采光约束(O_k≥O_j)、总成本约束(∑C_ijk≤2600万)，以及每户最多搬迁一次的完整性约束。
求解算法采用改进的贪心算法与模拟退火结合的方法。首先将院落按潜在腾空面积排序，优先处理能腾空大面积院落的搬迁组合。对每个候选院落，采用深度优先搜索寻找满足补偿条件的搬迁方案，计算边际收益。引入模拟退火机制避免陷入局部最优，以一定概率接受次优解。院落毗邻关系通过图论中的邻接矩阵表示，计算腾空院落的连通分量以获得毗邻加成收益。成本核算模块实时跟踪沟通成本、修缮成本和面积损失成本，确保方案在预算范围内。

问题三：性价比拐点分析
拐点分析需要建立成本收益的动态评估模型。定义性价比m=(ΔR×10)/(C_m+C_a+C_t)，其中ΔR为日租金增量，C_m为沟通成本，C_a为面积损失，C_t为时间成本。通过构造边际性价比函数dm/dn（n为搬迁户数），寻找函数极值点。当边际性价比降至行业基准回报率（20）时即为拐点。
建模时采用递推算法，按搬迁优先级逐步增加搬迁户数，每步计算：1)新增腾空整院面积及毗邻效应；2)租金增量现值（按10年折现）；3)边际成本增量。建立收益成本比的变化曲线，当曲线斜率等于1（即最后一单位投入带来一单位收益）时确定最优停止点。对于无法达到m≥20的情况，通过敏感性分析确定各参数临界值，计算使m达到20所需的最小租金增长率或最大成本压缩空间。
问题四：软件框架设计
软件系统采用模块化设计，核心是四层架构：数据层集成地理信息系统数据库，存储地块属性数据和空间关系；模型层封装补偿计算引擎和优化算法；服务层提供方案评估和对比功能；展示层实现交互式可视化。关键创新点是参数化建模框架，用户可通过调节补偿系数、成本权重等参数快速生成多种方案。
智能决策流程分为五步：1)数据清洗与拓扑构建，建立院落邻接关系图；2)搬迁可行性分析，标注符合补偿条件的搬迁对；3)多目标优化求解，生成Pareto最优解集；4)方案评估，计算各方案的成本收益指标；5)可视化呈现，支持方案对比和细节钻取。软件特别设计了情景模拟功能，允许用户手动调整搬迁方案并实时查看经济指标变化，辅助决策者理解方案敏感性。‘