算法与数据结构-（七）-CSDN博客

本文链接：https://blog.csdn.net/xbqztdjz/article/details/135241249

回溯算法

我们如同迷宫中的探索者，在前进的道路上可能会遇到困难。回溯的力量让我们能够重新开始，不断尝试，最终找到通往光明的出口。

回溯算法

回溯算法（backtrackingalgorithm）是一种通过穷举来解决问题的方法，它的核心思想是从一个初始状态出发，暴力搜索所有可能的解决方案，当遇到正确的解则将其记录，直到找到解或者尝试了所有可能的选择都无法找到解为止。回溯算法通常采用“深度优先搜索”来遍历解空间。在二叉树章节中，我们提到前序、中序和后序遍历都属于深度优先搜索。接下来，我们利用前序遍历构造一个回溯问题，逐步了解回溯算法的工作原理。

给定一个二叉树，搜索并记录所有值为7的节点，请返回节点列表。

对于此题，我们前序遍历这颗树，并判断当前节点的值是否为7，若是则将该节点的值加入到结果列表 res 之中。相关过程实现如图13‑1和以下代码所示。

 /* 前序遍历：例题一 */
 void preOrder(TreeNode *root) {
 if (root == nullptr) {
 return;
 }
 if (root->val == 7) {
 // 记录解
res.push_back(root);
 }
 preOrder(root->left);
 preOrder(root->right);
 }

尝试与回退

之所以称之为回溯算法，是因为该算法在搜索解空间时会采用“尝试”与“回退”的策略。

当算法在搜索过程中遇到某个状态无法继续前进或无法得到满足条件的解时，它会撤销上一步的选择，退回到之前的状态，并尝试其他可能的选择。

对于例题一，访问每个节点都代表一次“尝试”，而越过叶结点或返回父节点的 return 则表示“回退”。值得说明的是，回退并不仅仅包括函数返回。

为解释这一点，我们对例题一稍作拓展。例题二在二叉树中搜索所有值为7的节点，请返回根节点到这些节点的路径。

 /* 前序遍历：例题二 */
 void preOrder(TreeNode *root) {
 if (root == nullptr) {
 return;
 }
 // 尝试
path.push_back(root);
 if (root->val == 7) {
// 记录解
res.push_back(path);
 }
 preOrder(root->left);
 preOrder(root->right);
 // 回退
path.pop_back();
 }

在每次“尝试”中，我们通过将当前节点添加进 path 中弹出，以恢复本次尝试之前的状态。 path 来记录路径；而在“回退”前，我们可以将尝试和回退理解为“前进”与“撤销”，两个操作是互为逆向的。

剪枝

复杂的回溯问题通常包含一个或多个约束条件，约束条件通常可用于“剪枝”

例题三在二叉树中搜索所有值为7的节点，请返回根节点到这些节点的路径，并要求路径中不包含值为3的节点。

为了满足以上约束条件，我们需要添加剪枝操作：在搜索过程中，若遇到值为3的节点，则提前返回，停止继续搜索

/ === File: preorder_traversal_iii_compact.cpp ===
 /* 前序遍历：例题三 */
 void preOrder(TreeNode *root) {
 // 剪枝
if (root == nullptr || root->val == 3) {
 return;
 }
 // 尝试
path.push_back(root);
 if (root->val == 7) {
 // 记录解
res.push_back(path);
 }
 preOrder(root->left);
 preOrder(root->right);
 // 回退
path.pop_back();
 }

框架代码

接下来，我们尝试将回溯的“尝试、回退、剪枝”的主体框架提炼出来，提升代码的通用性。在以下框架代码中， state 表示问题的当前状态，choices 表示当前状态下可以做出的选择。

 /*回溯算法框架*/
 void backtrack(State *state, vector<Choice*> &choices, vector<State *>&res) {
 //判断是否为解
if(isSolution(state)) {
 //记录解
recordSolution(state, res);
 //停止继续搜索
return;
 }
 //遍历所有选择
for (Choice choice : choices) {
 //剪枝：判断选择是否合法
if(isValid(state, choice)){
 //尝试：做出选择，更新状态
makeChoice(state, choice);
 backtrack(state, choices, res);
 //回退：撤销选择，恢复到之前的状态
undoChoice(state, choice);
 }
 }
 }

接下来，我们基于框架代码来解决例题三。状态state为节点遍历路径，选择choices为当前节点的左子节点和右子节点，结果res是路径列表。

 /*判断当前状态是否为解*/
 bool isSolution(vector<TreeNode*> &state) {
 return!state.empty()&& state.back()->val == 7;
 }
 /*记录解*/
 void recordSolution(vector<TreeNode*> &state, vector<vector<TreeNode*>> &res) {
 res.push_back(state);
 }
 /*判断在当前状态下，该选择是否合法*/
 bool isValid(vector<TreeNode*>&state, TreeNode*choice){
 returnchoice !=nullptr &&choice->val !=3;
 }
 /*更新状态*/
 void makeChoice(vector<TreeNode*> &state, TreeNode *choice) {
 state.push_back(choice);
 }
/*恢复状态*/
 void undoChoice(vector<TreeNode*> &state, TreeNode *choice) {
 state.pop_back();
 }
 /*回溯算法：例题三*/
 void backtrack(vector<TreeNode*>&state, vector<TreeNode*> &choices, vector<vector<TreeNode*>> &res) {
 //检查是否为解
if(isSolution(state)) {
 //记录解
recordSolution(state, res);
 }
 //遍历所有选择
for (TreeNode *choice: choices) {
 //剪枝：检查选择是否合法
if(isValid(state, choice)){
 //尝试：做出选择，更新状态
makeChoice(state, choice);
 //进行下一轮选择
vector<TreeNode*> nextChoices{choice->left, choice->right};
 backtrack(state, nextChoices, res);
 //回退：撤销选择，恢复到之前的状态
undoChoice(state, choice);
 }
 }
 }

根据题意，我们在找到值为7的节点后应该继续搜索，因此需要将记录解之后的return语句删除。对比了保留或删除return语句的搜索过程。

相比基于前序遍历的代码实现，基于回溯算法框架的代码实现虽然显得啰嗦，但通用性更好。实际上，许多回溯问题都可以在该框架下解决。我们只需根据具体问题来定义 state 和 choices ，并实现框架中的各个方法即可。

优势与局限性

回溯算法本质上是一种深度优先搜索算法，它尝试所有可能的解决方案直到找到满足条件的解。这种方法的优势在于它能够找到所有可能的解决方案，而且在合理的剪枝操作下，具有很高的效率。然而，在处理大规模或者复杂问题时，回溯算法的运行效率可能难以接受。

‧ 时间：回溯算法通常需要遍历状态空间的所有可能，时间复杂度可以达到指数阶或阶乘阶。

‧ 空间：在递归调用中需要保存当前的状态（例如路径、用于剪枝的辅助变量等），当深度很大时，空间需求可能会变得很大。

即便如此，回溯算法仍然是某些搜索问题和约束满足问题的最佳解决方案。对于这些问题，由于无法预测哪些选择可生成有效的解，因此我们必须对所有可能的选择进行遍历。在这种情况下，关键是如何进行效率优化，常见的效率优化方法有两种。

‧ 剪枝：避免搜索那些肯定不会产生解的路径，从而节省时间和空间。

‧ 启发式搜索：在搜索过程中引入一些策略或者估计值，从而优先搜索最有可能产生有效解的路径。

回溯典型例题

搜索问题：这类问题的目标是找到满足特定条件的解决方案。

‧ 全排列问题：给定一个集合，求出其所有可能的排列组合。

‧ 子集和问题：给定一个集合和一个目标和，找到集合中所有和为目标和的子集。

‧ 汉诺塔问题：给定三个柱子和一系列大小不同的圆盘，要求将所有圆盘从一个柱子移动到另一个柱子，每次只能移动一个圆盘，且不能将大圆盘放在小圆盘上。

约束满足问题：这类问题的目标是找到满足所有约束条件的解。

‧ 𝑛皇后：在𝑛×𝑛的棋盘上放置𝑛个皇后，使得它们互不攻击。

‧ 数独：在9×9的网格中填入数字1~9，使得每行、每列和每个3×3子网格中的数字不重复。

‧ 图着色问题：给定一个无向图，用最少的颜色给图的每个顶点着色，使得相邻顶点颜色不同。

组合优化问题：这类问题的目标是在一个组合空间中找到满足某些条件的最优解。

‧ 0‑1背包问题：给定一组物品和一个背包，每个物品有一定的价值和重量，要求在背包容量限制内，选择物品使得总价值最大。

‧ 旅行商问题：在一个图中，从一个点出发，访问所有其他点恰好一次后返回起点，求最短路径。

‧ 最大团问题：给定一个无向图，找到最大的完全子图，即子图中的任意两个顶点之间都有边相连。

请注意，对于许多组合优化问题，回溯都不是最优解决方案。

‧ 0‑1背包问题通常使用动态规划解决，以达到更高的时间效率。

‧ 旅行商是一个著名的NP‑Hard问题，常用解法有遗传算法和蚁群算法等。

‧ 最大团问题是图论中的一个经典问题，可用贪心等启发式算法来解决。

全排列问题

全排列问题是回溯算法的一个典型应用。它的定义是在给定一个集合（如一个数组或字符串）的情况下，找出这个集合中元素的所有可能的排列。

输入一个整数数组，数组中不包含重复元素，返回所有可能的排列。

从回溯算法的角度看，我们可以把生成排列的过程想象成一系列选择的结果。假设输入数组为[1,2,3]，如果我们先选择1、再选择3、最后选择2，则获得排列[1,3,2]。回退表示撤销一个选择，之后继续尝试其他选择。从回溯代码的角度看，候选集合 choices 是输入数组中的所有元素，状态请注意，每个元素只允许被选择一次，因此 state 是直至目前已被选择的元素。 state 中的所有元素都应该是唯一的。如图13‑5所示，我们可以将搜索过程展开成一个递归树，树中的每个节点代表当前状态 state 。从根节点开始，经过三轮选择后到达叶节点，每个叶节点都对应一个排列。

重复选择剪枝

为了实现每个元素只被选择一次，我们考虑引入一个布尔型数组 selected，其中 selected[i]表示 choices[i] 是否已被选择，并基于它实现以下剪枝操作。

‧ 在做出选择choice[i] 后，我们就将 selected[i] 赋值为 True ，代表它已被选择。

‧ 遍历选择列表choices 时，跳过所有已被选择过的节点，即剪枝。

 /* 回溯算法：全排列 I */
 ↪
 void backtrack(vector<int> &state, const vector<int> &choices, vector<bool> &selected, vector<vector<int>>
 &res) {
 // 当状态长度等于元素数量时，记录解
if (state.size() == choices.size()) {
 res.push_back(state);
 return;
 }
 // 遍历所有选择
for (int i = 0; i < choices.size(); i++) {
 int choice = choices[i];
 // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
if (!selected[i]) {
 // 尝试：做出选择，更新状态
selected[i] = true;
 state.push_back(choice);
 // 进行下一轮选择
backtrack(state, choices, selected, res);
 // 回退：撤销选择，恢复到之前的状态
selected[i] = false;
 state.pop_back();
 }
 }
 }
 /* 全排列 I */
 vector<vector<int>> permutationsI(vector<int> nums) {
 vector<int> state;
 vector<bool> selected(nums.size(), false);
 vector<vector<int>> res;
 backtrack(state, nums, selected, res);
 return res;
 }

考虑相等元素的情况

输入一个整数数组，数组中可能包含重复元素，返回所有不重复的排列。

假设输入数组为[1,1,2]。为了方便区分两个重复元素1，我们将第二个1记为1。那么如何去除重复的排列呢？最直接地，考虑借助一个哈希表，直接对排列结果进行去重。然而这样做不够优雅，因为生成重复排列的搜索分支是没有必要的，应当被提前识别并剪枝，这样可以进一步提升算法效率。

本质上看，我们的目标是在某一轮选择中，保证多个相等的元素仅被选择一次。

在上一题的代码的基础上，我们考虑在每一轮选择中开启一个哈希表duplicated ，用于记录该轮中已经尝试过的元素，并将重复元素剪枝。

/* 回溯算法：全排列 II */
 ↪
 duplicated ，用于记录该轮中已经尝试
void backtrack(vector<int> &state, const vector<int> &choices, vector<bool> &selected, vector<vector<int>>
 &res) {
 // 当状态长度等于元素数量时，记录解
if (state.size() == choices.size()) {
 res.push_back(state);
 return;
 }
 // 遍历所有选择
unordered_set<int> duplicated;
 for (int i = 0; i < choices.size(); i++) {
 int choice = choices[i];
 // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
if (!selected[i] && duplicated.find(choice) == duplicated.end()) {
 // 尝试：做出选择，更新状态
duplicated.emplace(choice); // 记录选择过的元素值
selected[i] = true;
 state.push_back(choice);
 // 进行下一轮选择
backtrack(state, choices, selected, res);
 // 回退：撤销选择，恢复到之前的状态
selected[i] = false;
 state.pop_back();
 }
 }
 }
 /* 全排列 II */
 vector<vector<int>> permutationsII(vector<int> nums) {
 vector<int> state;
 vector<bool> selected(nums.size(), false);
 vector<vector<int>> res;
 backtrack(state, nums, selected, res);
 return res;
 }

假设元素两两之间互不相同，则𝑛个元素共有𝑛!种排列（阶乘）；在记录结果时，需要复制长度为𝑛的列表，使用𝑂(𝑛)时间。因此时间复杂度为𝑂(𝑛!𝑛)。

最大递归深度为𝑛，使用𝑂(𝑛)栈帧空间。 selected 使用 𝑂(𝑛)空间。同一时刻最多共有𝑛个 duplicated ，使用𝑂(𝑛2)空间。因此空间复杂度为𝑂(𝑛2)。

两种剪枝对比

请注意，虽然 selected 和 duplicated 都用作剪枝，但两者的目标是不同的。

‧ 重复选择剪枝：整个搜索过程中只有一个 selected 。它记录的是当前状态中包含哪些元素，作用是避免某个元素在 state 中重复出现。

‧ 相等元素剪枝：每轮选择（即每个开启的 backtrack 函数）都包含一个duplicated 。它记录的是在遍历中哪些元素已被选择过，作用是保证相等元素只被选择一次。

注意，树中的每个节点代表一个选择，从根节点到叶节点的路径上的各个节点构成一个排列。

子集和问题

无重复元素的情况

给定一个正整数数组元素和等于 nums 和一个目标正整数 target ，请找出所有可能的组合，使得组合中的 target 。给定数组无重复元素，每个元素可以被选取多次。请以列表形式返回这些组合，列表中不应包含重复组合。

/*回溯算法：子集和I*/
 voidbacktrack(vector<int>&state,inttarget,inttotal,vector<int>&choices,vector<vector<int>>&res){
 //子集和等于target时，记录解
if(total ==target) {
 res.push_back(state);
 return;
 }
 //遍历所有选择
for (size_t i = 0; i < choices.size();i++) {
 //剪枝：若子集和超过target，则跳过该选择
if(total + choices[i] > target){
 continue;
 }
 //尝试：做出选择，更新元素和total
 state.push_back(choices[i]);
 //进行下一轮选择
backtrack(state, target, total +choices[i],choices, res);
 //回退：撤销选择，恢复到之前的状态
state.pop_back();
 }
 }
 /*求解子集和I（包含重复子集）*/
 vector<vector<int>> subsetSumINaive(vector<int> &nums, int target) {
 vector<int> state; //状态（子集）
int total = 0; //子集和
vector<vector<int>>res; //结果列表（子集列表）
backtrack(state, target, total, nums, res);
 returnres;
 }

重复子集剪枝

def backtrack(
 state: list[int], target: int, choices: list[int], start: int, res: list[list[int]]
 ):
 """ 回溯算法：子集和 I"""
 # 子集和等于 target 时，记录解
if target == 0:
 res.append(list(state))
 return
 # 遍历所有选择
# 剪枝二：从 start 开始遍历，避免生成重复子集
for i in range(start, len(choices)):
 # 剪枝一：若子集和超过 target ，则直接结束循环
 # 这是因为数组已排序，后边元素更大，子集和一定超过 target
 if target- choices[i] < 0:
 break
 # 尝试：做出选择，更新 target, start
 state.append(choices[i])
 # 进行下一轮选择
backtrack(state, target- choices[i], choices, i, res)
 # 回退：撤销选择，恢复到之前的状态
state.pop()
 def subset_sum_i(nums: list[int], target: int)-> list[list[int]]:
 """ 求解子集和 I"""
 state = [] # 状态（子集）
nums.sort() # 对 nums 进行排序
start = 0 # 遍历起始点
res = [] # 结果列表（子集列表）
backtrack(state, target, nums, start, res)
 return res

重复子集剪枝

/* 回溯算法：子集和 I */
 void backtrack(vector<int> &state, int target, vector<int> &choices, int start, vector<vector<int>> &res) {
 // 子集和等于 target 时，记录解
if (target == 0) {
 res.push_back(state);
 return;
 }
 // 遍历所有选择
// 剪枝二：从 start 开始遍历，避免生成重复子集
for (int i = start; i < choices.size(); i++) {
 // 剪枝一：若子集和超过 target ，则直接结束循环
// 这是因为数组已排序，后边元素更大，子集和一定超过 target
 if (target- choices[i] < 0) {
 break;
 }
 // 尝试：做出选择，更新 target, start
 state.push_back(choices[i]);
 // 进行下一轮选择
backtrack(state, target- choices[i], choices, i, res);
 // 回退：撤销选择，恢复到之前的状态
state.pop_back();
 }
 }
 /* 求解子集和 I */
 vector<vector<int>> subsetSumI(vector<int> &nums, int target) {
 vector<int> state;
 vector<vector<int>> res;
 }
 // 状态（子集）
sort(nums.begin(), nums.end()); // 对 nums 进行排序
int start = 0;
 // 遍历起始点
// 结果列表（子集列表）
backtrack(state, target, nums, start, res);
 return res;

考虑重复元素的情况

 /* 回溯算法：子集和 II */
 void backtrack(vector<int> &state, int target, vector<int> &choices, int start, vector<vector<int>> &res) {
 // 子集和等于 target 时，记录解
if (target == 0) {
 res.push_back(state);
 return;
 }
 // 遍历所有选择
// 剪枝二：从 start 开始遍历，避免生成重复子集
// 剪枝三：从 start 开始遍历，避免重复选择同一元素
for (int i = start; i < choices.size(); i++) {
 // 剪枝一：若子集和超过 target ，则直接结束循环
// 这是因为数组已排序，后边元素更大，子集和一定超过 target
 if (target- choices[i] < 0) {
 break;
 }
 // 剪枝四：如果该元素与左边元素相等，说明该搜索分支重复，直接跳过
if (i > start && choices[i] == choices[i- 1]) {
 continue;
 }
 // 尝试：做出选择，更新 target, start
 state.push_back(choices[i]);
 // 进行下一轮选择
backtrack(state, target- choices[i], choices, i + 1, res);
 // 回退：撤销选择，恢复到之前的状态
state.pop_back();
 }
 }
 /* 求解子集和 II */
 vector<vector<int>> subsetSumII(vector<int> &nums, int target) {
 vector<int> state;
 // 状态（子集）
sort(nums.begin(), nums.end()); // 对 nums 进行排序
int start = 0;
 vector<vector<int>> res;
 // 遍历起始点
// 结果列表（子集列表）
backtrack(state, target, nums, start, res);
 return res;
 }

N皇后问题

列与对角线剪枝

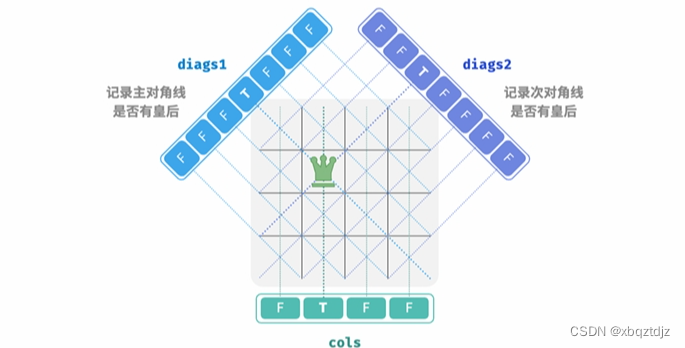
为了满足列约束，我们可以利用一个长度为𝑛的布尔型数组前，我们通过 cols 记录每一列是否有皇后。在每次决定放置 cols 将已有皇后的列进行剪枝，并在回溯中动态更新 cols 的状态。那么，如何处理对角线约束呢？设棋盘中某个格子的行列索引为(𝑟𝑜𝑤,𝑐𝑜𝑙)，选定矩阵中的某条主对角线，我们发现该对角线上所有格子的行索引减列索引都相等，即对角线上所有格子的𝑟𝑜𝑤−𝑐𝑜𝑙为恒定值。也就是说，如果两个格子满足𝑟𝑜𝑤1−𝑐𝑜𝑙1 =𝑟𝑜𝑤2−𝑐𝑜𝑙2，则它们一定处在同一条主对角线上。利用该规律，我们可以借助图13‑18所示的数组 diag1 ，记录每条主对角线上是否有皇后。同理，次对角线上的所有格子的𝑟𝑜𝑤+𝑐𝑜𝑙是恒定值。我们同样也可以借助数组diag2来处理次对角线约束。

/* 回溯算法：N 皇后 */
 ↪
 void backtrack(int row, int n, vector<vector<string>> &state, vector<vector<vector<string>>> &res,
 vector<bool> &cols,
 vector<bool> &diags1, vector<bool> &diags2) {
 // 当放置完所有行时，记录解
if (row == n) {
 res.push_back(state);
 return;
 }
 // 遍历所有列
for (int col = 0; col < n; col++) {
 // 计算该格子对应的主对角线和副对角线
int diag1 = row- col + n- 1;
 int diag2 = row + col;
 // 剪枝：不允许该格子所在列、主对角线、副对角线存在皇后
if (!cols[col] && !diags1[diag1] && !diags2[diag2]) {
 // 尝试：将皇后放置在该格子
state[row][col] = "Q";
 cols[col] = diags1[diag1] = diags2[diag2] = true;
 // 放置下一行
backtrack(row + 1, n, state, res, cols, diags1, diags2);
 // 回退：将该格子恢复为空位
state[row][col] = "#";
 cols[col] = diags1[diag1] = diags2[diag2] = false;
 }
 }
 }
 /* 求解 N 皇后 */
 vector<vector<vector<string>>> nQueens(int n) {
 // 初始化 n*n 大小的棋盘，其中 'Q' 代表皇后，'#' 代表空位
vector<vector<string>> state(n, vector<string>(n, "#"));
 vector<bool> cols(n, false);
 // 记录列是否有皇后
vector<bool> diags1(2 * n- 1, false); // 记录主对角线是否有皇后
vector<bool> diags2(2 * n- 1, false); // 记录副对角线是否有皇后
vector<vector<vector<string>>> res;
 backtrack(0, n, state, res, cols, diags1, diags2);
 return res;
 }

逐行放置𝑛次，考虑列约束，则从第一行到最后一行分别有𝑛、𝑛−1、…、2、1个选择，因此时间复杂度为𝑂(𝑛!)。实际上，根据对角线约束的剪枝也能够大幅地缩小搜索空间，因而搜索效率往往优于以上时间复杂度。

数组state使用𝑂(𝑛2)空间，数组cols、 diags1 和diags2 皆使用𝑂(𝑛)空间。最大递归深度为𝑛，使用

$O\left ( n \right )$ 栈帧空间。因此，空间复杂度为 $o\left ( n ^{2}\right )$ 。