分治算法——（六）

xbqztdjz

已于 2023-12-27 09:11:44 修改

阅读量357

点赞数 9

文章标签：算法

于 2023-12-26 11:36:25 首次发布

本文链接：https://blog.csdn.net/xbqztdjz/article/details/135216118

版权

分治

难题被逐层拆解，每一次的拆解都使它变得更为简单。分而治之揭示了一个重要的事实：从简单做起，一切都不再复杂。

分治算法

分治（divideandconquer），全称分而治之，是一种非常重要且常见的算法策略。分治通常基于递归实现，包括“分”和“治”两个步骤。

1. 分（划分阶段）：递归地将原问题分解为两个或多个子问题，直至到达最小子问题时终止。

2. 治（合并阶段）：从已知解的最小子问题开始，从底至顶地将子问题的解进行合并，从而构建出原问题的解。

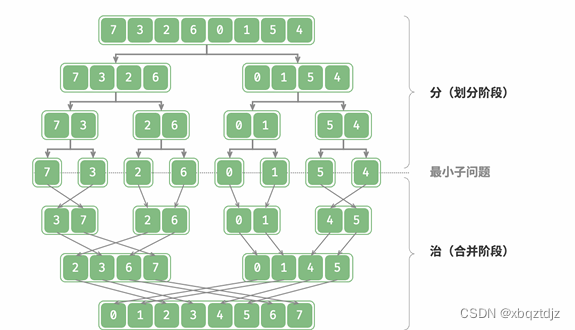
“归并排序”是分治策略的典型应用之一。

1. 分：递归地将原数组（原问题）划分为两个子数组（子问题），直到子数组只剩一个元素（最小子问题）。

2. 治：从底至顶地将有序的子数组（子问题的解）进行合并，从而得到有序的原数组（原问题的解）。

如何判断分治问题

一个问题是否适合使用分治解决，通常可以参考以下几个判断依据。

1. 问题可以被分解：原问题可以被分解成规模更小、类似的子问题，以及能够以相同方式递归地进行划分。

2. 子问题是独立的：子问题之间是没有重叠的，互相没有依赖，可以被独立解决。

3. 子问题的解可以被合并：原问题的解通过合并子问题的解得来。

显然，归并排序是满足以上三条判断依据的。

1. 问题可以被分解：递归地将数组（原问题）划分为两个子数组（子问题）。

2. 子问题是独立的：每个子数组都可以独立地进行排序（子问题可以独立进行求解）。

3. 子问题的解可以被合并：两个有序子数组（子问题的解）可以被合并为一个有序数组（原问题的解）

通过分治提升效率

分治不仅可以有效地解决算法问题，往往还可以带来算法效率的提升。在排序算法中，快速排序、归并排序、堆排序相较于选择、冒泡、插入排序更快，就是因为它们应用了分治策略。那么，我们不禁发问：为什么分治可以提升算法效率，其底层逻辑是什么？换句话说，将大问题分解为多个子问题、解决子问题、将子问题的解合并为原问题的解，这几步的效率为什么比直接解决原问题的效率更高？这个问题可以从操作数量和并行计算两方面来讨论。

操作数量优化

以“冒泡排序”为例，其处理一个长度为𝑛的数组需要𝑂(𝑛2)时间。假设我们按照图12‑2所示的方式，将数组从中点分为两个子数组，则划分需要𝑂(𝑛)时间，排序每个子数组需要𝑂((𝑛/2)2)时间，合并两个子数组需要𝑂(𝑛)时间。总体时间复杂度为：

$O(\frac{n^{2}}{2}+2n)$

$n^{2}>O(\frac{n^{2}}{2}+2n)$

这意味着当𝑛>4时，划分后的操作数量更少，排序效率应该更高。请注意，划分后的时间复杂度仍然是平方阶𝑂(𝑛2)，只是复杂度中的常数项变小了。

并行计算优化

我们知道，分治生成的子问题是相互独立的，因此通常可以并行解决。也就是说，分治不仅可以降低算法的时间复杂度，还有利于操作系统的并行优化。并行优化在多核或多处理器的环境中尤其有效，因为系统可以同时处理多个子问题，更加充分地利用计算资源，从而显著减少总体的运行时间。比如在“桶排序”中，我们将海量的数据平均分配到各个桶中，则可所有桶的排序任务分散到各个计算单元，完成后再进行结果合并。

分治搜索策略

搜索算法分为两大类。

‧ 暴力搜索：它通过遍历数据结构实现，时间复杂度为𝑂(𝑛)。

‧ 自适应搜索：它利用特有的数据组织形式或先验信息，可达到𝑂(log𝑛)甚至𝑂(1)的时间复杂度。实际上，时间复杂度为𝑂(log𝑛)的搜索算法通常都是基于分治策略实现的，例如二分查找和树。

‧ 二分查找的每一步都将问题（在数组中搜索目标元素）分解为一个小问题（在数组的一半中搜索目标元素），这个过程一直持续到数组为空或找到目标元素为止。

‧ 树是分治关系的代表，在二叉搜索树、AVL树、堆等数据结构中，各种操作的时间复杂度皆为𝑂(log𝑛) 。

二分查找的分治策略如下所示。

‧ 问题可以被分解：二分查找递归地将原问题（在数组中进行查找）分解为子问题（在数组的一半中进行查找），这是通过比较中间元素和目标元素来实现的。

‧ 子问题是独立的：在二分查找中，每轮只处理一个子问题，它不受另外子问题的影响。

‧ 子问题的解无须合并：二分查找旨在查找一个特定元素，因此不需要将子问题的解进行合并。当子问题得到解决时，原问题也会同时得到解决。

分治能够提升搜索效率，本质上是因为暴力搜索每轮只能排除一个选项，而分治搜索每轮可以排除一半选项。

基于分治实现二分

二分查找是基于递推（迭代）实现的。现在我们基于分治（递归）来实现它。

从分治角度，我们将搜索区间[𝑖,𝑗]对应的子问题记为𝑓(𝑖,𝑗)。从原问题𝑓(0,𝑛−1)为起始点，通过以下步骤进行二分查找。

1. 计算搜索区间[𝑖,𝑗]的中点𝑚，根据它排除一半搜索区间。

2. 递归求解规模减小一半的子问题，可能为𝑓(𝑖,𝑚−1)或𝑓(𝑚+1,𝑗)。

3. 循环第1.和2.步，直至找到 target 或区间为空时返回。

图12‑4 展示了在数组中二分查找元素6的分治过程。

在实现代码中，我们声明一个递归函数 dfs() 来求解问题𝑓(𝑖,𝑗)。

 /* 二分查找：问题 f(i, j) */
 int dfs(vector<int> &nums, int target, int i, int j) {
 // 若区间为空，代表无目标元素，则返回-1
 if (i > j) {
 return-1;
 }
 // 计算中点索引 m
 int m = (i + j) / 2;
 if (nums[m] < target) {
 // 递归子问题 f(m+1, j)
 return dfs(nums, target, m + 1, j);
 } else if (nums[m] > target) {
 // 递归子问题 f(i, m-1)
 return dfs(nums, target, i, m- 1);
 } else {
 // 找到目标元素，返回其索引
return m;
 }
 }
 /* 二分查找 */
 int binarySearch(vector<int> &nums, int target) {
 int n = nums.size();
 // 求解问题 f(0, n-1)
 return dfs(nums, target, 0, n- 1);

构建二叉树问题

给定一个二叉树的前序遍历preorder 和中序遍历 inorder ，请从中构建二叉树，返回二叉树的根节点。

根据以上分析，这道题是可以使用分治来求解的，但如何通过前序遍历preorder 和中序遍历 inorder 来划分左子树和右子树呢？

根据定义， preorder 和 inorder 都可以被划分为三个部分。

‧ 前序遍历： preorder 和中序遍历 inorder 来划分 [ 根节点 | 左子树 | 右子树 ]，例如图12‑5的树对应 [ 3 | 9 | 2 1 7 ]。

‧ 中序遍历： [ 左子树 | 根节点｜右子树 ]，例如图12‑5的树对应 [ 9 | 3 | 1 2 7 ]。

以上图数据为例，我们可以通过图所示的步骤得到划分结果。

1. 前序遍历的首元素3是根节点的值。

2.查找根节点3在inorder 中的索引，利用该索引可将inorder 划分为[ 9 | 3 ｜ 1 2 7 ]。

3.根据inorder 划分结果，易得左子树和右子树的节点数量分别为1和3，从而可将 preorder 划分为

[ 3 | 9 | 2 1 7 ]。

/* 构建二叉树：分治 */
 ↪
 inorder 中元素到索引的映射。
TreeNode *dfs(vector<int> &preorder, vector<int> &inorder, unordered_map<int, int> &hmap, int i, int l,
 int r) {
//子树区间为空时终止
if(r-l < 0)
 returnNULL;
 //初始化根节点
TreeNode*root= new TreeNode(preorder[i]);
 //查询m，从而划分左右子树
int m = hmap[preorder[i]];
 //子问题：构建左子树
root->left= dfs(preorder, inorder, hmap, i + 1, l, m-1);
 //子问题：构建右子树
root->right = dfs(preorder, inorder,hmap, i + 1 + m-l, m + 1, r);
 //返回根节点
returnroot;
 }
 /*构建二叉树*/
 TreeNode*buildTree(vector<int> &preorder, vector<int> &inorder) {
 //初始化哈希表，存储inorder元素到索引的映射
unordered_map<int, int> hmap;
 for (int i = 0; i <inorder.size(); i++) {
 hmap[inorder[i]]= i;
 }
 TreeNode*root= dfs(preorder, inorder, hmap, 0, 0, inorder.size()-1);
 returnroot;
 }

每个递归函数内的前序遍历preorder 和中序遍历 inorder 的划分结果

设树的节点数量为𝑛，初始化每一个节点（执行一个递归函数dfs() ）使用𝑂(1)时间。因此总体时间复杂度为𝑂(𝑛)。

哈希表存储inorder 元素到索引的映射，空间复杂度为𝑂(𝑛)。最差情况下，即二叉树退化为链表时，递归深度达到𝑛，使用𝑂(𝑛)的栈帧空间。因此总体空间复杂度为𝑂(𝑛)

汉诺塔问题

在归并排序和构建二叉树中，我们都是将原问题分解为两个规模为原问题一半的子问题。然而对于汉诺塔问题，我们采用不同的分解策略。

给定三根柱子，记为A、B和C。起始状态下，柱子A上套着𝑛个圆盘，它们从上到下按照从小到大的顺序排列。我们的任务是要把这𝑛个圆盘移到柱子C上，并保持它们的原有顺序不变。在移动圆盘的过程中，需要遵守以下规则。

1. 圆盘只能从一个柱子顶部拿出，从另一个柱子顶部放入。

2. 每次只能移动一个圆盘。

3. 小圆盘必须时刻位于大圆盘之上。

我们将规模为𝑖的汉诺塔问题记做𝑓(𝑖)

将原问题𝑓(𝑛)划分为两个子问题𝑓(𝑛−1) 和一个子问题𝑓(1)，并按照以下顺序解决这三个子问题。

1. 将𝑛−1个圆盘借助C从A移至B。

2. 将剩余1个圆盘从A直接移至C。

3. 将𝑛−1个圆盘借助A从B移至C。对于这两个子问题𝑓(𝑛−1)，可以通过相同的方式进行递归划分，直至达到最小子问题𝑓(1)。而𝑓(1)的解是已知的，只需一次移动操作即可。

代码实现

在代码中，我们声明一个递归函数 dfs(i, src, buf, tar) ，它的作用是将柱src 顶部的𝑖个圆盘借助缓冲柱buf移动至目标柱tar

 void move(vector<int> &src, vector<int> &tar) {
 //从src顶部拿出一个圆盘
int pan = src.back();
 src.pop_back();
 //将圆盘放入tar顶部
tar.push_back(pan);
 }
 /*求解汉诺塔：问题f(i)*/
 void dfs(int i, vector<int> &src, vector<int> &buf, vector<int> &tar) {
 //若src只剩下一个圆盘，则直接将其移到tar
 if(i ==1) {
 move(src, tar);
 return;
 }
 //子问题f(i-1)：将src顶部i-1个圆盘借助tar移到buf
 dfs(i-1, src, tar, buf);
 //子问题f(1)：将src剩余一个圆盘移到tar
 move(src, tar);
 //子问题f(i-1)：将buf顶部i-1个圆盘借助src移到tar
 dfs(i-1, buf, src, tar);
 }
 /*求解汉诺塔*/
 void solveHanota(vector<int> &A, vector<int> &B, vector<int> &C) {
 int n = A.size();
 //将A顶部n个圆盘借助B移到C
 dfs(n, A, B, C);
 }

汉诺塔问题形成一个高度为𝑛的递归树，每个节点代表一个子问题、对应一个开启的dfs() 函数，因此时间复杂度为𝑂(2𝑛)，空间复杂度为𝑂(𝑛)。

汉诺塔问题源自一种古老的传说故事。在古印度的一个寺庙里，僧侣们有三根高大的钻石柱子，以及64个大小不一的金圆盘。僧侣们不断地移动原盘，他们相信在最后一个圆盘被正确放置的那一刻，这个世界就会结束。

然而，即使僧侣们每秒钟移动一次，总共需要大约264 ≈1.84×1019秒，合约5850亿年，远远超过了现在对宇宙年龄的估计。所以，倘若这个传说是真的，我们应该不需要担心世界末日的到来。