排序
排序犹如一把将混乱变为秩序的魔法钥匙,使我们能以更高效的方式理解与处理数据。 无论是简单的升序,还是复杂的分类排列,排序都向我们展示了数据的和谐美感。
排序算法
排序算法 (sorting algorithm)用于对一组数据按照特定顺序进行排列。排序算法有着广泛的应用,因为有序数据通常能够被更有效地查找、分析和处理。排序算法中的数据类型可以是整数、浮点数、字符或字符串等。排序的判断规则可根据需求设定,如数字大小、字符 ASCII 码顺序或自定义规则。
评价维度
运行效率:我们期望排序算法的时间复杂度尽量低,且总体操作数量较少(即时间复杂度中的常数项降低)。 对于大数据量情况,运行效率显得尤为重要。
就地性:顾名思义,(原地排序)通过在原数组上直接操作实现排序,无须借助额外的辅助数组,从而节省内存。通常情况下,原地排序的数据搬运操作较少,运行速度也更快。
稳定性:稳定排序在完成排序后,相等元素在数组中的相对顺序不发生改变。
稳定排序是多级排序场景的必要条件。假设我们有一个存储学生信息的表格,第 1 列和第 2 列分别是姓名和 年龄。在这种情况下,非稳定排序可能导致输入数据的有序性丧失。
自适应性:「自适应排序」的时间复杂度会受输入数据的影响,即最佳、最差、平均时间复杂度并不完全相 等。自适应性需要根据具体情况来评估。如果最差时间复杂度差于平均时间复杂度,说明排序算法在某些数据下性能可能劣化,因此被视为负面属性;而如果最佳时间复杂度优于平均时间复杂度,则被视为正面属性。
是否基于比较:「基于比较的排序」依赖于比较运算符(<,=,>)来判断元素的相对顺序,从而排序整个数组,理论最优时间复杂度为 𝑂(𝑛 log 𝑛) 。而「非比较排序」不使用比较运算符,时间复杂度可达 𝑂(𝑛) , 但其通用性相对较差。
理想排序算法
运行快、原地、稳定、正向自适应、通用性好。显然,迄今为止尚未发现兼具以上所有特性的排序算法。因 此,在选择排序算法时,需要根据具体的数据特点和问题需求来决定。
选择排序
选择排序 (selection sort)的工作原理非常直接:开启一个循环,每轮从未排序区间选择最小的元素,将其 放到已排序区间的末尾。设数组的长度为 𝑛 。
算法流程
1. 初始状态下,所有元素未排序,即未排序(索引)区间为 [0, 𝑛 − 1] 。
2. 选取区间 [0, 𝑛 − 1] 中的最小元素,将其与索引 0 处元素交换。完成后,数组前 1 个元素已排序。
3. 选取区间 [1, 𝑛 − 1] 中的最小元素,将其与索引 1 处元素交换。完成后,数组前 2 个元素已排序。
4. 以此类推。经过 𝑛 − 1 轮选择与交换后,数组前 𝑛 − 1 个元素已排序。 5. 仅剩的一个元素必定是最大元素,无须排序,因此数组排序完成。
在代码中,我们用 𝑘 来记录未排序区间内的最小元素。
/* 选择排序 */
void selectionSort(vector<int> &nums) {
int n = nums.size();
// 外循环:未排序区间为 [i, n-1]
for (int i = 0; i < n - 1; i++) {
// 内循环:找到未排序区间内的最小元素
int k = i;
for (int j = i + 1; j < n; j++) {
if (nums[j] < nums[k])
k = j; // 记录最小元素的索引
}
// 将该最小元素与未排序区间的首个元素交换
swap(nums[i], nums[k]);
}
}算法特性
时间复杂度为 𝑂( )、非自适应排序:外循环共 𝑛 − 1 轮,第一轮的未排序区间长度为 𝑛 ,最后一轮 的未排序区间长度为 2 ,即各轮外循环分别包含 𝑛、𝑛 − 1、…、3、2 轮内循环,求和为
空间复杂度 𝑂(1)、原地排序:指针 𝑖 和 𝑗 使用常数大小的额外空间。
非稳定排序:如图 11‑3 所示,元素 nums[i] 有可能被交换至与其相等的元素的右边,导致两者相对顺 序发生改变。
冒泡排序
冒泡排序 (bubble sort)通过连续地比较与交换相邻元素实现排序。这个过程就像气泡从底部升到顶部一样, 因此得名冒泡排序。
冒泡过程可以利用元素交换操作来模拟:从数组最左端开始向右遍历,依次比较相邻元素大 小,如果“左元素 > 右元素”就交换它俩。遍历完成后,最大的元素会被移动到数组的最右端。
算法流程
设数组的长度为 𝑛 ,冒泡排序的步骤如图 11‑5 所示。
1. 首先,对 𝑛 个元素执行“冒泡”,将数组的最大元素交换至正确位置,
2. 接下来,对剩余 𝑛 − 1 个元素执行“冒泡”,将第二大元素交换至正确位置。
3. 以此类推,经过 𝑛 − 1 轮“冒泡”后,前 𝑛 − 1 大的元素都被交换至正确位置。
4. 仅剩的一个元素必定是最小元素,无须排序,因此数组排序完成。
/* 冒泡排序 */
void bubbleSort(vector<int> &nums) {
// 外循环:未排序区间为 [0, i]
for (int i = nums.size() - 1; i > 0; i--) {
// 内循环:将未排序区间 [0, i] 中的最大元素交换至该区间的最右端
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
// 交换 nums[j] 与 nums[j + 1]
// 这里使用了 std::swap() 函数
swap(nums[j], nums[j + 1]);
}
}
}
}效率优化
我们发现,如果某轮“冒泡”中没有执行任何交换操作,说明数组已经完成排序,可直接返回结果。因此,可 以增加一个标志位 flag 来监测这种情况,一旦出现就立即返回。 经过优化,冒泡排序的最差和平均时间复杂度仍为 𝑂(𝑛2 ) ;但当输入数组完全有序时,可达到最佳时间复 杂度 𝑂(𝑛) 。
void bubbleSortWithFlag(vector<int> &nums) {
// 外循环:未排序区间为 [0, i]
for (int i = nums.size() - 1; i > 0; i--) {
bool flag = false; // 初始化标志位
// 内循环:将未排序区间 [0, i] 中的最大元素交换至该区间的最右端
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
// 交换 nums[j] 与 nums[j + 1]
// 这里使用了 std::swap() 函数
swap(nums[j], nums[j + 1]);
flag = true; // 记录交换元素
}
}
if (!flag)
break; // 此轮冒泡未交换任何元素,直接跳出
}
}算法特性
‧ 时间复杂度为 𝑂(𝑛2 )、自适应排序:各轮“冒泡”遍历的数组长度依次为 𝑛 − 1、𝑛 − 2、…、2、1 , 总和为 (𝑛 − 1)𝑛/2 。在引入 flag 优化后,最佳时间复杂度可达到 𝑂(𝑛) 。
‧ 空间复杂度为 𝑂(1)、原地排序:指针 𝑖 和 𝑗 使用常数大小的额外空间。
‧ 稳定排序:由于在“冒泡”中遇到相等元素不交换。
插入排序
插入排序 (insertion sort)是一种简单的排序算法,它的工作原理与手动整理一副牌的过程非常相似。 具体来说,我们在未排序区间选择一个基准元素,将该元素与其左侧已排序区间的元素逐一比较大小,并将 该元素插入到正确的位置。
算法流程
1. 初始状态下,数组的第 1 个元素已完成排序。
2. 选取数组的第 2 个元素作为 base ,将其插入到正确位置后,数组的前 2 个元素已排序。
3. 选取第 3 个元素作为 base ,将其插入到正确位置后,数组的前 3 个元素已排序。
4. 以此类推,在最后一轮中,选取最后一个元素作为 base ,将其插入到正确位置后,所有元素均已排序。
void insertionSort(vector<int> &nums) {
// 外循环:已排序元素数量为 1, 2, ..., n
for (int i = 1; i < nums.size(); i++) {
int base = nums[i], j = i - 1;
// 内循环:将 base 插入到已排序部分的正确位置
while (j >= 0 && nums[j] > base) {
nums[j + 1] = nums[j]; // 将 nums[j] 向右移动一位
j--;
}
nums[j + 1] = base; // 将 base 赋值到正确位置
}
}算法特性 ‧
时间复杂度 𝑂(𝑛2 )、自适应排序:最差情况下,每次插入操作分别需要循环 𝑛 − 1、𝑛 − 2、…、2、1 次,求和得到 (𝑛 − 1)𝑛/2 ,因此时间复杂度为 𝑂(𝑛2 ) 。在遇到有序数据时,插入操作会提前终止。 当输入数组完全有序时,插入排序达到最佳时间复杂度 𝑂(𝑛) 。
‧ 空间复杂度 𝑂(1)、原地排序:指针 𝑖 和 𝑗 使用常数大小的额外空间。
‧ 稳定排序:在插入操作过程中,我们会将元素插入到相等元素的右侧,不会改变它们的顺序。
插入排序优势
插入排序的时间复杂度为 𝑂(𝑛2 ) ,而我们即将学习的快速排序的时间复杂度为 𝑂(𝑛 log 𝑛) 。尽管插入排序的时间复杂度相比快速排序更高,但在数据量较小的情况下,插入排序通常更快。
这个结论与线性查找和二分查找的适用情况的结论类似。快速排序这类 𝑂(𝑛 log 𝑛) 的算法属于基于分治的 排序算法,往往包含更多单元计算操作。而在数据量较小时,𝑛 2 和 𝑛 log 𝑛 的数值比较接近,复杂度不占主导作用;每轮中的单元操作数量起到决定性因素。
实际上,许多编程语言(例如 Java)的内置排序函数都采用了插入排序,大致思路为:对于长数组,采用基 于分治的排序算法,例如快速排序;对于短数组,直接使用插入排序。
虽然冒泡排序、选择排序和插入排序的时间复杂度都为 𝑂(𝑛2 ) ,但在实际情况中,插入排序的使用频率显著高于冒泡排序和选择排序,主要有以下原因。
‧ 冒泡排序基于元素交换实现,需要借助一个临时变量,共涉及 3 个单元操作;插入排序基于元素赋值实现,仅需 1 个单元操作。因此,冒泡排序的计算开销通常比插入排序更高。
‧ 选择排序在任何情况下的时间复杂度都为 𝑂(𝑛2 ) 。如果给定一组部分有序的数据,插入排序通常比选择排序效率更高。 ‧ 选择排序不稳定,无法应用于多级排序。
快速排序
快速排序 (quick sort)是一种基于分治策略的排序算法,运行高效,应用广泛。
哨兵划分
快速排序的核心操作是“哨兵划分”,其目标是:选择数组中的某个元素作为“基准数”,将所有小于基准数的元素移到其左侧,而大于基准数的元素移到其右侧。
具体来说,哨兵划分的流程如下。
1. 选取数组最左端元素作为基准数,初始化两个指针 i 和 j 分别指向数组的两端。
2. 设置一个循环,在每轮中使用 i(j)分别寻找第一个比基准数大(小)的元素,然后交换这两个元素。
3. 循环执行步骤 2. ,直到 i 和 j 相遇时停止,最后将基准数交换至两个子数组的分界线。
哨兵划分完成后,原数组被划分成三部分:左子数组、基准数、右子数组,且满足“左子数组任意元素 ≤ 基 准数 ≤ 右子数组任意元素”。因此,我们接下来只需对这两个子数组进行排序。
/* 元素交换 */
void swap(vector<int> &nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
/* 哨兵划分 */
int partition(vector<int> &nums, int left, int right) {
// 以 nums[left] 作为基准数
int i = left, j = right;
while (i < j) {
while (i < j && nums[j] >= nums[left])
j--; // 从右向左找首个小于基准数的元素
while (i < j && nums[i] <= nums[left])
i++; // 从左向右找首个大于基准数的元素
swap(nums, i, j); // 交换这两个元素
}
swap(nums, i, left); // 将基准数交换至两子数组的分界线
return i; // 返回基准数的索引
}算法流程
1. 首先,对原数组执行一次“哨兵划分”,得到未排序的左子数组和右子数组。
2. 然后,对左子数组和右子数组分别递归执行“哨兵划分”。
3. 持续递归,直至子数组长度为 1 时终止,从而完成整个数组的排序。
/* 快速排序 */
void quickSort(vector<int> &nums, int left, int right) {
// 子数组长度为 1 时终止递归
if (left >= right)
return;
// 哨兵划分
int pivot = partition(nums, left, right);
// 递归左子数组、右子数组
quickSort(nums, left, pivot - 1);
quickSort(nums, pivot + 1, right);
}
算法特性
‧ 时间复杂度 𝑂(𝑛 log 𝑛)、自适应排序:在平均情况下,哨兵划分的递归层数为 log 𝑛 ,每层中的总循环数为 𝑛 ,总体使用 𝑂(𝑛 log 𝑛) 时间。在最差情况下,每轮哨兵划分操作都将长度为 𝑛 的数组划分为长度为 0 和 𝑛−1 的两个子数组,此时递归层数达到 𝑛 层,每层中的循环数为 𝑛 ,总体使用 𝑂() 时间。
‧ 空间复杂度 𝑂(𝑛)、原地排序:在输入数组完全倒序的情况下,达到最差递归深度 𝑛 ,使用 𝑂(𝑛) 栈帧 空间。排序操作是在原数组上进行的,未借助额外数组。
‧ 非稳定排序:在哨兵划分的最后一步,基准数可能会被交换至相等元素的右侧。
基准数优化
快速排序在某些输入下的时间效率可能降低。举一个极端例子,假设输入数组是完全倒序的,由于我们选择 最左端元素作为基准数,那么在哨兵划分完成后,基准数被交换至数组最右端,导致左子数组长度为 𝑛 − 1、 右子数组长度为 0 。如此递归下去,每轮哨兵划分后的右子数组长度都为 0 ,分治策略失效,快速排序退化 为“冒泡排序”。
为了尽量避免这种情况发生,我们可以优化哨兵划分中的基准数的选取策略。例如,我们可以随机选取一个 元素作为基准数。然而,如果运气不佳,每次都选到不理想的基准数,效率仍然不尽如人意。 需要注意的是,编程语言通常生成的是“伪随机数”。如果我们针对伪随机数序列构建一个特定的测试样例, 那么快速排序的效率仍然可能劣化。
为了进一步改进,我们可以在数组中选取三个候选元素(通常为数组的首、尾、中点元素),并将这三个候选 元素的中位数作为基准数。这样一来,基准数“既不太小也不太大”的概率将大幅提升。当然,我们还可以 选取更多候选元素,以进一步提高算法的稳健性。采用这种方法后,时间复杂度劣化至 𝑂(𝑛2 ) 的概率大大 降低
/* 选取三个元素的中位数 */
int medianThree(vector<int> &nums, int left, int mid, int right) {
// 此处使用异或运算来简化代码
// 异或规则为 0 ^ 0 = 1 ^ 1 = 0, 0 ^ 1 = 1 ^ 0 = 1
if ((nums[left] < nums[mid]) ^ (nums[left] < nums[right]))
return left;
else if ((nums[mid] < nums[left]) ^ (nums[mid] < nums[right]))
return mid;
else
return right;
}
/* 哨兵划分(三数取中值) */
int partition(vector<int> &nums, int left, int right) {
// 选取三个候选元素的中位数
int med = medianThree(nums, left, (left + right) / 2, right);
// 将中位数交换至数组最左端
swap(nums, left, med);
// 以 nums[left] 作为基准数
int i = left, j = right;
while (i < j) {
while (i < j && nums[j] >= nums[left])
j--; // 从右向左找首个小于基准数的元素
while (i < j && nums[i] <= nums[left])
i++; // 从左向右找首个大于基准数的元素
swap(nums, i, j); // 交换这两个元素
}
swap(nums, i, left); // 将基准数交换至两子数组的分界线
return i; // 返回基准数的索引
}
尾递归优化
在某些输入下,快速排序可能占用空间较多。为了防止栈帧空间的累积,我们可以在每轮哨兵排序完成后,比较两个子数组的长度,仅对较短的子数组进 行递归。由于较短子数组的长度不会超过 𝑛/2 ,因此这种方法能确保递归深度不超过 log 𝑛 ,从而将最差空 间复杂度优化至 𝑂(log 𝑛) 。
/* 快速排序(尾递归优化) */
void quickSort(vector<int> &nums, int left, int right) {
// 子数组长度为 1 时终止
while (left < right) {
// 哨兵划分操作
int pivot = partition(nums, left, right);
// 对两个子数组中较短的那个执行快排
if (pivot - left < right - pivot) {
quickSort(nums, left, pivot - 1); // 递归排序左子数组
left = pivot + 1; // 剩余未排序区间为 [pivot + 1, right]
} else {
quickSort(nums, pivot + 1, right); // 递归排序右子数组
right = pivot - 1; // 剩余未排序区间为 [left, pivot - 1]
}
}
}
归并排序
归并排序(mergesort)是一种基于分治策略的排序算法,包含“划分”和“合并”阶段。
1. 划分阶段:通过递归不断地将数组从中点处分开,将长数组的排序问题转换为短数组的排序问题。
2. 合并阶段:当子数组长度为1时终止划分,开始合并,持续地将左右两个较短的有序数组合并为一个较 长的有序数组,直至结束。
算法流程
“划分阶段”从顶至底递归地将数组从中点切分为两个子数组。
1. 计算数组中点 mid ,递归划分左子数组(区间 [left, mid] )和右子数组(区间 [mid + 1, right] )
2. 递归执行步骤1.,直至子数组区间长度为1时,终止递归划分。 “合并阶段”从底至顶地将左子数组和右子数组合并为一个有序数组。
需要注意的是,从长度为1的子数组开 始合并,合并阶段中的每个子数组都是有序的。
观察发现,归并排序与二叉树后序遍历的递归顺序是一致的。
‧后序遍历:先递归左子树,再递归右子树,最后处理根节点。
‧归并排序:先递归左子数组,再递归右子数组,最后处理合并。
/*合并左子数组和右子数组*/
//左子数组区间[left, mid]
//右子数组区间[mid+ 1, right]
void merge(vector<int> &nums, int left, int mid, int right) {
//初始化辅助数组
vector<int> tmp(nums.begin() + left,nums.begin() + right+ 1);
//左子数组的起始索引和结束索引
int leftStart = left-left, leftEnd= mid-left;
//右子数组的起始索引和结束索引
int rightStart = mid + 1-left, rightEnd= right-left;
//i,j分别指向左子数组、右子数组的首元素
int i = leftStart, j = rightStart;
//通过覆盖原数组nums来合并左子数组和右子数组
for (int k = left; k <=right; k++) {
//若“左子数组已全部合并完”,则选取右子数组元素,并且j++
if(i > leftEnd)
nums[k] = tmp[j++];
//否则,若“右子数组已全部合并完”或“左子数组元素<=右子数组元素”,则选取左子数组元素,并且i++
elseif (j > rightEnd|| tmp[i] <=tmp[j])
nums[k] = tmp[i++];
//否则,若“左右子数组都未全部合并完”且“左子数组元素>右子数组元素”,则选取右子数组元素,并且j++
else
nums[k] = tmp[j++];
}
}
/*归并排序*/
void mergeSort(vector<int> &nums, int left, int right) {
// 终止条件
if (left >= right)
return; // 当子数组长度为 1 时终止递归
// 划分阶段
int mid = (left + right) / 2;
// 计算中点
mergeSort(nums, left, mid);
// 递归左子数组
mergeSort(nums, mid + 1, right); // 递归右子数组
// 合并阶段
merge(nums, left, mid, right);
}算法特性
‧ 时间复杂度𝑂(𝑛log𝑛)、非自适应排序:划分产生高度为log𝑛的递归树,每层合并的总操作数量为 n,因此总体时间复杂度为𝑂(𝑛log𝑛)。
‧ 空间复杂度𝑂(𝑛)、非原地排序:递归深度为log𝑛,使用𝑂(log𝑛)大小的栈帧空间。合并操作需要借助辅助数组实现,使用𝑂(𝑛)大小的额外空间。
‧ 稳定排序:在合并过程中,相等元素的次序保持不变。
链表排序*
对于链表,归并排序相较于其他排序算法具有显著优势,可以将链表排序任务的空间复杂度优化至𝑂(1)。
‧ 划分阶段:可以通过使用“迭代”替代“递归”来实现链表划分工作,从而省去递归使用的栈帧空间。 ‧ 合并阶段:在链表中,节点增删操作仅需改变引用(指针)即可实现,因此合并阶段(将两个短有序链 表合并为一个长有序链表)无须创建额外链表。
具体实现细节比较复杂,有兴趣的可以查阅相关资料进行学习。
堆排序
堆排序(heapsort)是一种基于堆数据结构实现的高效排序算法。
我们可以利用已经学过的“建堆操作”和 “元素出堆操作”实现堆排序。
1. 输入数组并建立小顶堆,此时最小元素位于堆顶。
2. 不断执行出堆操作,依次记录出堆元素,即可得到从小到大排序的序列。
以上方法虽然可行,但需要借助一个额外数组来保存弹出的元素,比较浪费空间。
在实际中,我们通常使用 一种更加优雅的实现方式。在代码实现中,我们使用了与堆章节相同的从顶至底堆化 sift_down() 函数。值得注意的是,由于堆的长度 会随着提取最大元素而减小,因此我们需要给 sift_down() 函数添加一个长度参数𝑛,用于指定堆的当前有 效长度。
/* 堆的长度为 n ,从节点 i 开始,从顶至底堆化 */
void siftDown(vector<int> &nums, int n, int i) {
while (true) {
// 判断节点 i, l, r 中值最大的节点,记为 ma
int l = 2 * i + 1;
int r = 2 * i + 2;
int ma = i;
if (l < n && nums[l] > nums[ma])
ma = l;
if (r < n && nums[r] > nums[ma])
ma = r;
// 若节点 i 最大或索引 l, r 越界,则无须继续堆化,跳出
if (ma == i) {
break;
}
// 交换两节点
swap(nums[i], nums[ma]);
// 循环向下堆化
i = ma;
}
}
/* 堆排序 */
void heapSort(vector<int> &nums) {
// 建堆操作:堆化除叶节点以外的其他所有节点
for (int i = nums.size() / 2- 1; i >= 0;--i) {
siftDown(nums, nums.size(), i);
}
// 从堆中提取最大元素,循环 n-1 轮
for (int i = nums.size()- 1; i > 0;--i) {
// 交换根节点与最右叶节点(即交换首元素与尾元素)
swap(nums[0], nums[i]);
// 以根节点为起点,从顶至底进行堆化
siftDown(nums, i, 0);
}
}算法特性
‧ 时间复杂度𝑂(𝑛log𝑛)、非自适应排序:建堆操作使用𝑂(𝑛)时间。从堆中提取最大元素的时间复杂 度为𝑂(log𝑛),共循环𝑛−1轮。
‧ 空间复杂度𝑂(1)、原地排序:几个指针变量使用𝑂(1)空间。元素交换和堆化操作都是在原数组上进行的。
‧ 非稳定排序:在交换堆顶元素和堆底元素时,相等元素的相对位置可能发生变化。
桶排序
前述的几种排序算法都属于“基于比较的排序算法”,它们通过比较元素间的大小来实现排序。此类排序算法的时间复杂度无法超越𝑂(𝑛log𝑛)。接下来,我们将探讨几种“非比较排序算法”,它们的时间复杂度可以达到线性阶。
桶排序(bucketsort)是分治策略的一个典型应用。它通过设置一些具有大小顺序的桶,每个桶对应一个数据范围,将数据平均分配到各个桶中;然后,在每个桶内部分别执行排序;最终按照桶的顺序将所有数据合并。
算法流程
考虑一个长度为𝑛的数组,元素是范围[0,1)的浮点数。
1. 初始化𝑘个桶,将𝑛个元素分配到𝑘个桶中。
2. 对每个桶分别执行排序(本文采用编程语言的内置排序函数)。
3. 按照桶的从小到大的顺序,合并结果。
/* 桶排序 */
void bucketSort(vector<float> &nums) {
// 初始化 k = n/2 个桶,预期向每个桶分配 2 个元素
int k = nums.size() / 2
vector<vector<float>> buckets(k);
// 1. 将数组元素分配到各个桶中
for (float num : nums) {
// 输入数据范围 [0, 1),使用 num * k 映射到索引范围 [0, k-1]
int i = num * k;
// 将 num 添加进桶 bucket_idx
buckets[i].push_back(num);
}
// 2. 对各个桶执行排序
for (vector<float> &bucket : buckets) {
// 使用内置排序函数,也可以替换成其他排序算法
sort(bucket.begin(), bucket.end());
}
// 3. 遍历桶合并结果
int i = 0;
for (vector<float> &bucket : buckets) {
for (float num : bucket) {
nums[i++] = num;
}
}
}算法特性
桶排序适用于处理体量很大的数据。例如,输入数据包含100万个元素,由于空间限制,系统内存无法一次 性加载所有数据。此时,可以将数据分成1000个桶,然后分别对每个桶进行排序,最后将结果合并。
‧ 时间复杂度𝑂(𝑛+𝑘):假设元素在各个桶内平均分布,那么每个桶内的元素数量为𝑛 𝑘。假设排序单 个桶使用𝑂(𝑛 𝑘 log 𝑛𝑘)时间,则排序所有桶使用𝑂(𝑛log𝑛 𝑘)时间。当桶数量𝑘比较大时,时间复杂度 则趋向于𝑂(𝑛)。合并结果时需要遍历所有桶和元素,花费𝑂(𝑛+𝑘)时间。
‧ 自适应排序:在最坏情况下,所有数据被分配到一个桶中,且排序该桶使用𝑂(𝑛2)时间。
‧ 空间复杂度𝑂(𝑛+𝑘)、非原地排序:需要借助𝑘个桶和总共𝑛个元素的额外空间。
‧ 桶排序是否稳定取决于排序桶内元素的算法是否稳定。
如何实现平均分配
桶排序的时间复杂度理论上可以达到𝑂(𝑛),关键在于将元素均匀分配到各个桶中,因为实际数据往往不是均匀分布的。例如,我们想要将淘宝上的所有商品按价格范围平均分配到10个桶中,但商品价格分布不均, 低于100元的非常多,高于1000元的非常少。若将价格区间平均划分为10份,各个桶中的商品数量差距会非常大。 为实现平均分配,我们可以先设定一个大致的分界线,将数据粗略地分到3个桶中。分配完毕后,再将商品较多的桶继续划分为3个桶,直至所有桶中的元素数量大致相等。
如下图所示,这种方法本质上是创建一个递归树,目标是让叶节点的值尽可能平均。当然,不一定要每轮将数据划分为3个桶,具体划分方式可根据数据特点灵活选择。
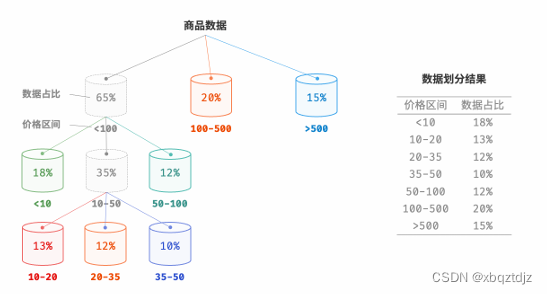
如果我们提前知道商品价格的概率分布,则可以根据数据概率分布设置每个桶的价格分界线。值得注意的是,数据分布并不一定需要特意统计,也可以根据数据特点采用某种概率模型进行近似。
如下图所示,我们假设商品价格服从正态分布,这样就可以合理地设定价格区间,从而将商品平均分配到各个桶中。
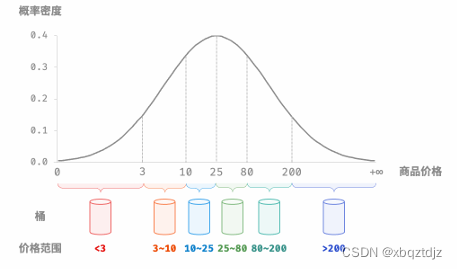
计数排序
计数排序(countingsort)通过统计元素数量来实现排序,通常应用于整数数组。
简单实现
先来看一个简单的例子。给定一个长度为𝑛的数组其中的元素都是“非负整数”,计数排序的整体流
程如下。
遍历数组,找出数组中的最大数字,记为𝑚,然后创建一个长度为𝑚+1的辅助数组counter 。
借助counter 统计 nums 中各数字的出现次数,其中counter[num] 对应数字num 的出现次数。统计方法很简单,只需遍历 nums(设当前数字为 num),每轮将num 的出现次数。统计方法 counter[num]增加 1 即可
3. 由于counter的各个索引天然有序,因此相当于所有数字已经被排序好了。接下来,我们遍历counter,根据各数字的出现次数,将它们按从小到大的顺序填入 nums 即可。
/* 计数排序 */
// 简单实现,无法用于排序对象
void countingSortNaive(vector<int> &nums) {
// 1. 统计数组最大元素 m
int m = 0;
for (int num : nums) {
m = max(m, num);
}
// 2. 统计各数字的出现次数
// counter[num] 代表 num 的出现次数
vector<int> counter(m + 1, 0);
for (int num : nums) {
counter[num]++;
}
// 3. 遍历 counter ,将各元素填入原数组 nums
int i = 0;
for (int num = 0; num < m + 1; num++) {
for (int j = 0; j < counter[num]; j++, i++) {
nums[i] = num;
}
}
}计数排序与桶排序的联系从桶排序的角度看,我们可以将计数排序中的计数数组counter 的每个索引视为一个桶,将统计数量的过程看作是将各个元素分配到对应的桶中。本质上,计数排序是桶排序在整型数据下的一个特例。
完整实现
如果输入数据是对象,上述步骤3.就失效了。假设输入数据是商品对象,我们想要按 照商品价格(类的成员变量)对商品进行排序,而上述算法只能给出价格的排序结果。
前缀和具有明确的意义,prefix[num]-1代表元素在结果数组 res 中最后一次出现的索引。
每个元素num,在每轮迭代中执行以下两步。
1. 将num填入数组 res 的索引
2. 令前缀和 prefix[num]- 1 处。 prefix[num] 减小 1 ,从而得到下次放置 num 的索引。
遍历完成后,数组res中就是排序好的结果,最后使用 res 覆盖原数组 nums 的 nums 即可。
def counting_sort(nums: list[int]):
"""计数排序"""
#完整实现,可排序对象,并且是稳定排序
#1.统计数组最大元素m
m = max(nums)
#2.统计各数字的出现次数
#counter[num]代表num的出现次数
counter = [0] * (m+ 1)
for num innums:
counter[num] +=1
#3.求counter的前缀和,将“出现次数”转换为“尾索引”
#即counter[num]-1是num在res中最后一次出现的索引
for i inrange(m):
counter[i + 1] +=counter[i]
#4.倒序遍历nums,将各元素填入结果数组res
#初始化数组res用于记录结果
n = len(nums)
res = [0] * n
for i inrange(n-1,-1,-1):
num = nums[i]
res[counter[num]-1] = num #将num放置到对应索引处
counter[num]-= 1 # 令前缀和自减 1 ,得到下次放置 num 的索引
# 使用结果数组 res 覆盖原数组 nums
for i in range(n):
nums[i] = res[i]算法特性
‧ 时间复杂度𝑂(𝑛+𝑚):涉及遍历 nums 和遍历 counter ,都使用线性时间。一般情况下𝑛≫𝑚,时 间复杂度趋于𝑂(𝑛)。
‧ 空间复杂度𝑂(𝑛+𝑚)、非原地排序:借助了长度分别为𝑛和𝑚的数组 counter 。
‧ 稳定排序:由于向res中填充元素的顺序是“从右向左”的,因此倒序遍历 res 和 nums 可以避免改变相等元素之间的相对位置,从而实现稳定排序。实际上,正序遍历 nums 也可以得到正确的排序结果,但结果是非稳定的。
局限性
看到这里,你也许会觉得计数排序非常巧妙,仅通过统计数量就可以实现高效的排序工作。然而,使用计数排序的前置条件相对较为严格。 计数排序只适用于非负整数。若想要将其用于其他类型的数据,需要确保这些数据可以被转换为非负整数, 并且在转换过程中不能改变各个元素之间的相对大小关系。例如,对于包含负数的整数数组,可以先给所有 数字加上一个常数,将全部数字转化为正数,排序完成后再转换回去即可。 计数排序适用于数据量大但数据范围较小的情况。比如,在上述示例中𝑚不能太大,否则会占用过多空间。 而当𝑛≪𝑚时,计数排序使用𝑂(𝑚)时间,可能比𝑂(𝑛log𝑛)的排序算法还要慢。
基数排序
上一节我们介绍了计数排序,它适用于数据量𝑛较大但数据范围𝑚较小的情况。假设我们需要对𝑛=106 个学号进行排序,而学号是一个8位数字,这意味着数据范围𝑚=108非常大,使用计数排序需要分配大 量内存空间,而基数排序可以避免这种情况。
基数排序(radixsort)的核心思想与计数排序一致,也通过统计个数来实现排序。在此基础上,基数排序利 用数字各位之间的递进关系,依次对每一位进行排序,从而得到最终的排序结果。
算法流程
以学号数据为例,假设数字的最低位是第1位,最高位是第8位,基数排序的流程如图11‑18所示。 1. 初始化位数𝑘=1。 2. 对学号的第𝑘位执行“计数排序”。完成后,数据会根据第𝑘位从小到大排序。 3. 将𝑘增加1,然后返回步骤2,继续迭代,直到所有位都排序完成后结束。
/* 获取元素 num 的第 k 位,其中 exp = 10^(k-1) */
int digit(int num, int exp) {
// 传入 exp 而非 k 可以避免在此重复执行昂贵的次方计算
return (num / exp) % 10;
}
/* 计数排序(根据 nums 第 k 位排序) */
void countingSortDigit(vector<int> &nums, int exp) {
// 十进制的位范围为 0~9 ,因此需要长度为 10 的桶
vector<int> counter(10, 0);
int n = nums.size();
// 统计 0~9 各数字的出现次数
for (int i = 0; i < n; i++) {
int d = digit(nums[i], exp); // 获取 nums[i] 第 k 位,记为 d
counter[d]++;
// 统计数字 d 的出现次数
}
// 求前缀和,将“出现个数”转换为“数组索引”
for (int i = 1; i < 10; i++) {
counter[i] += counter[i- 1];
}
// 倒序遍历,根据桶内统计结果,将各元素填入 res
vector<int> res(n, 0);
for (int i = n- 1; i >= 0; i--) {
int d = digit(nums[i], exp);
int j = counter[d]- 1; // 获取 d 在数组中的索引 j
res[j] = nums[i];
// 将当前元素填入索引 j
counter[d]--;
}
// 使用结果覆盖原数组 nums
for (int i = 0; i < n; i++)
nums[i] = res[i];
}
/* 基数排序 */
// 将 d 的数量减 1
void radixSort(vector<int> &nums) {
// 获取数组的最大元素,用于判断最大位数
int m = *max_element(nums.begin(), nums.end());
// 按照从低位到高位的顺序遍历
for (int exp = 1; exp <= m; exp *= 10)
// 对数组元素的第 k 位执行计数排序
// k = 1-> exp = 1
// k = 2-> exp = 10
// 即 exp = 10^(k-1)
countingSortDigit(nums, exp);
}
为什么从最低位开始排序?
在连续的排序轮次中,后一轮排序会覆盖前一轮排序的结果。举例来说,如果第一轮排序a<b结果 a>𝑏,那么第二轮的结果将取代第一轮的结果。由于数字的高 位优先级高于低位,我们应该先排序低位再排序高位。
算法特性
相较于计数排序,基数排序适用于数值范围较大的情况,但前提是数据必须可以表示为固定位数的格式,且位 数不能过大。例如,浮点数不适合使用基数排序,因为其位数𝑘过大,可能导致时间复杂度𝑂(𝑛𝑘)≫𝑂(𝑛2) 。
‧ 时间复杂度𝑂(𝑛𝑘):设数据量为𝑛、数据为𝑑进制、最大位数为𝑘,则对某一位执行计数排序使用 𝑂(𝑛+𝑑)时间,排序所有𝑘位使用𝑂((𝑛+𝑑)𝑘)时间。通常情况下,𝑑和𝑘都相对较小,时间复杂 度趋向𝑂(𝑛)。
‧ 空间复杂度𝑂(𝑛+𝑑)、非原地排序:与计数排序相同,基数排序需要借助长度为𝑛和𝑑的数组 res 和counter。
‧ 稳定排序:与计数排序相同。
小结
重点回顾
‧ 冒泡排序通过交换相邻元素来实现排序。通过添加一个标志位来实现提前返回,我们可以将冒泡排序 的最佳时间复杂度优化到𝑂(𝑛)。 ‧ 插入排序每轮将未排序区间内的元素插入到已排序区间的正确位置,从而完成排序。虽然插入排序的 时间复杂度为𝑂(𝑛2),但由于单元操作相对较少,它在小数据量的排序任务中非常受欢迎。 ‧ 快速排序基于哨兵划分操作实现排序。在哨兵划分中,有可能每次都选取到最差的基准数,导致时间复 杂度劣化至𝑂(𝑛2)。引入中位数基准数或随机基准数可以降低这种劣化的概率。尾递归方法可以有效 地减少递归深度,将空间复杂度优化到𝑂(log𝑛)。 ‧ 归并排序包括划分和合并两个阶段,典型地体现了分治策略。在归并排序中,排序数组需要创建辅助数 组,空间复杂度为𝑂(𝑛);然而排序链表的空间复杂度可以优化至𝑂(1)。 ‧ 桶排序包含三个步骤:数据分桶、桶内排序和合并结果。它同样体现了分治策略,适用于数据体量很大 的情况。桶排序的关键在于对数据进行平均分配。 ‧ 计数排序是桶排序的一个特例,它通过统计数据出现的次数来实现排序。计数排序适用于数据量大但 数据范围有限的情况,并且要求数据能够转换为正整数。 ‧ 基数排序通过逐位排序来实现数据排序,要求数据能够表示为固定位数的数字。 ‧ 总的来说,我们希望找到一种排序算法,具有高效率、稳定、原地以及正向自适应性等优点。然而,正 如其他数据结构和算法一样,没有一种排序算法能够同时满足所有这些条件。在实际应用中,我们需要 根据数据的特性来选择合适的排序算法。 ‧ 图11‑19对比了主流排序算法的效率、稳定性、就地性和自适应性等。
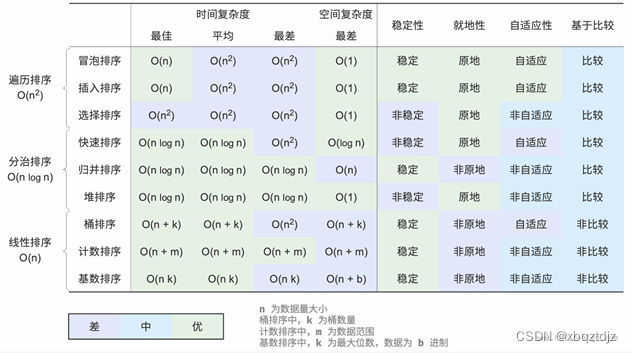





















 1721
1721











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








