【导数】学习笔记

闲着无聊，刚好最近复学导数，就来随手写一写学习笔记。

周所知众，学导数前需要知道一些极限的知识，所以我决定先讲一点极限的知识。

ps：在本文中可能会出现一些符号，这里列举两个会出现多次的符号：$()$ 表示不包括端点的区间，$[]$ 表示包括端点的区间，$\cup$ 表示交集。在导数的“运算与运算法则”中，$c$ 以及 $C$ 表示常数。

极限

这里只写了极限的定义与运算法则。

定义

极限描述的是在自变量的某一变化过程中，函数值的变化情况（废话）。

在此之前还得讲一些乱七八糟的东西：左、右邻域与去心邻域。

按照直接理解来说，邻域就是附近的区域。在这里，我们定义 $x_0$ 的邻域为一个区间：$(x_0-X,x_0+X)$，其中 $X$ 为一个正数（不过这个东西好像用不到）。

自然地，去心邻域指的就是不包括中心的邻域。我们定义 $x_0$ 的去心邻域为一个区间：$(x_0-X,x_0)\cup (x_0,x_0+X)$。左邻域就是指去心邻域的左区间，即 $(x_0-X,x_0)$。右邻域就是指去心邻域的右区间，即 $(x_0,x_0+X)$，其中 $X$ 为一个正数。

接下来就可以讲定义了。

极限还要分两类，一类是趋近于一个非无穷的常数，另一类是趋近于无穷，正无穷和负无穷。

先讲趋近常数的，定义是设函数 $f(x)$ 在 $x_0$ 的某个去心邻域内有定义，如果存在实数 $A$，使得 $\forall M>0$，都有一个数 $N>0$，使得当 $x\in (x_0-N,x_0)\cup (x_0,x_0+N)$ 时，有 $|f(x)-A|<M$，则称 $f(x)$ 在 $x_0$ 点处的极限为 $A$，记作 $\underset{x\to x_0}{\lim }f(x)=A$。

左极限的定义是设函数 $f(x)$ 在 $x_0$ 的某个左邻域内有定义，如果存在实数 $A$，使得 $\forall M>0$，都有一个数 $N>0$，使得当 $x\in (x_0-N,x_0)$ 时，有 $|f(x)-A|<M$，则称 $f(x)$ 在 $x_0$ 点处的左极限值为 $A$，记作 $\underset{x\to x_0-}{\lim }f(x)=A$。

类似地，可以定义右极限，记作 $\underset{x\to x_0+}{\lim }f(x)=A$。

当然 $\underset{x\to x_0}{\lim }f(x)$ 存在的前提条件是 $\underset{x\to x_0-}{\lim }f(x)$ 与 $\underset{x\to x_0+}{\lim }f(x)$ 都存在且他们相等。

接下来就是趋近于无穷的，定义是设函数 $f(x)$ 在 $x\in (-\infty ,-X)\cup (X,+\infty )$ 里有定义（$X$ 为某个正数），如果存在实数 $A$，使得 $\forall M>0$，都有一个数 $N>0$，使得当 $|x|>N$ 时，有 $|f(x)-A|<M$，则称 $x\to \infty$ 时 $f(x)$ 的极限为 $A$，记作 $\underset{x\to \infty }{\lim }f(x)=A$。

类似地，可以分别定义 $x\to -\infty$ 与 $x\to +\infty$ 时 $f(x)$ 的左侧极限 $\underset{x\to -\infty }{\lim }$ 和右侧极限 $\underset{x\to +\infty }{\lim }$。

当然 $\underset{x\to \infty }{\lim }f(x)$ 存在的前提条件是 $\underset{x\to -\infty }{\lim }f(x)$ 与 $\underset{x\to +\infty }{\lim }f(x)$ 都存在且他们相等。

p.s：这里不需要太深入了解定义，导数需要的只是简单的实际意义。除了了解定义外，只需要分清楚六种极限过程即可。

运算法则

设$\underset{x\to \square }{\lim }f(x)=A$，$\underset{x\to \square }{\lim }g(x)=B$。

则 $\underset{x\to \square }{\lim }[f(x)+g(x)]=A+B$，$\underset{x\to \square }{\lim }[f(x)-g(x)]=A-B$，$\underset{x\to \square }{\lim }f(x)\times g(x)=A\times B$，$\underset{x\to \square }{\lim }\frac{f(x)}{g(x)}=\frac{A}{B}(B\ne 0)$。

导数

概念（定义）

还得先讲一些没用的东西。

平均变化率：

一般地，已知函数 $y=f(x)$，$x_0$，$x_1$ 是其定义域中不同的两点，记 $\Delta x=x_1-x_0$，$\Delta y=y_1-y_0=f(x_1)-f(x_0)=f(x_0+\Delta x)-f(x_0)$。

则当 $\Delta x\ne 0$ 时，$\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\frac{\Delta y}{\Delta x}$ 称作函数在区间 $[x_0,x_0+\Delta x]$ （或 $[x_0+\Delta x,x_0]$）上的平均变化率。

瞬时变化率与导数：

设函数 $y=f(x)$ 在 $x_0$ 附近有定义，当自变量在 $x=x_0$ 附近改变量为 $\Delta x$ 时，函数值相应的改变，$\Delta y=f(x_0+\Delta x)-f(x_0)$。

当 $\Delta x$ 趋近于 $0$ 时，平均变化率会趋近于一个常数。设这个常数为 $l$，那么 $l$ 就被称为函数 $f(x)$ 在点 $x_0$ 的瞬时变化率。

当 $\Delta x$ 趋近于 $0$ 时，平均变化率 $\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$ 趋近于常数 $l$ 可以记作 $\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=l$。

函数在 $x_0$ 处的瞬时变化率，称为函数 $f(x)$ 在 $x_0$ 处的导数，记作 $f^{\prime }(x_0)$。

这时称 $f(x)$ 在 $x=x_0$ 处可导。

于是上述变化过程可以记作 $\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=f^{\prime }(x_0)$。

可导与导函数：

如果函数 $f(x)$ 在区间 $(a,b)$ 内每一点都是可导的，则称函数 $f(x)$ 在区间 $(a,b)$ 内可导。

这样，对区间 $(a,b)$ 内每一个值 $x$，都有一个确定的导数 $f^{\prime }(x)$。

于是，在区间 $(a,b)$ 内，$f^{\prime }(x)$ 构成一个新的函数，我们把这个函数称为函数 $y=f(x)$ 的导函数，记作 $f^{\prime }(x)$ 或 $y^{\prime }$。

p.s：导函数通常称为导数。如果不特别指明某一点的导数，那么求导数指的就是求导函数。

运算与运算法则

运算：

$(1)$ 若 $f(x)=c$，则 $f^{\prime }(x)=0$。

$(2)$ 若 $f(x)=x^a$，则 $f^{\prime }(x)=a{x}^{a-1}$。

$(3)$ 若 $f(x)=a^x$，则 $f^{\prime }(x)=a^x\ln a$。

$(4)$ 若 $f(x)={\log }_{a}x$，则 $f^{\prime }(x)=\frac{1}{x\ln a}$。

$(5)$ 若 $f(x)=\sin x$，则 $f^{\prime }(x)=\cos x$。

$(6)$ 若 $f(x)=\cos x$，则 $f^{\prime }(x)=-\sin x$。

运算法则：

$(f(x)\pm g(x){)}^{\prime }=f^{\prime }(x)\pm g^{\prime }(x)$

$[f(x)g(x){]}^{\prime }=f^{\prime }(x)g(x)+f(x)g^{\prime }(x)$

$[Cf(x){]}^{\prime }=C{f}^{\prime }(x)$

$[\frac{f(x)}{g(x)}{]}^{\prime }=\frac{g(x)f^{\prime }(x)-f(x)g^{\prime }(x)}{g^2(x)}(g(x)\ne 0)$

复合函数求导：

对于可导函数 $y=f(u)$，$u=u(x)$，$f_x^{\prime }=\frac{df}{dx}=\frac{df}{du}\times \frac{du}{dx}=f_u^{\prime }{u}_x^{\prime }$。

导数的应用

几何意义：

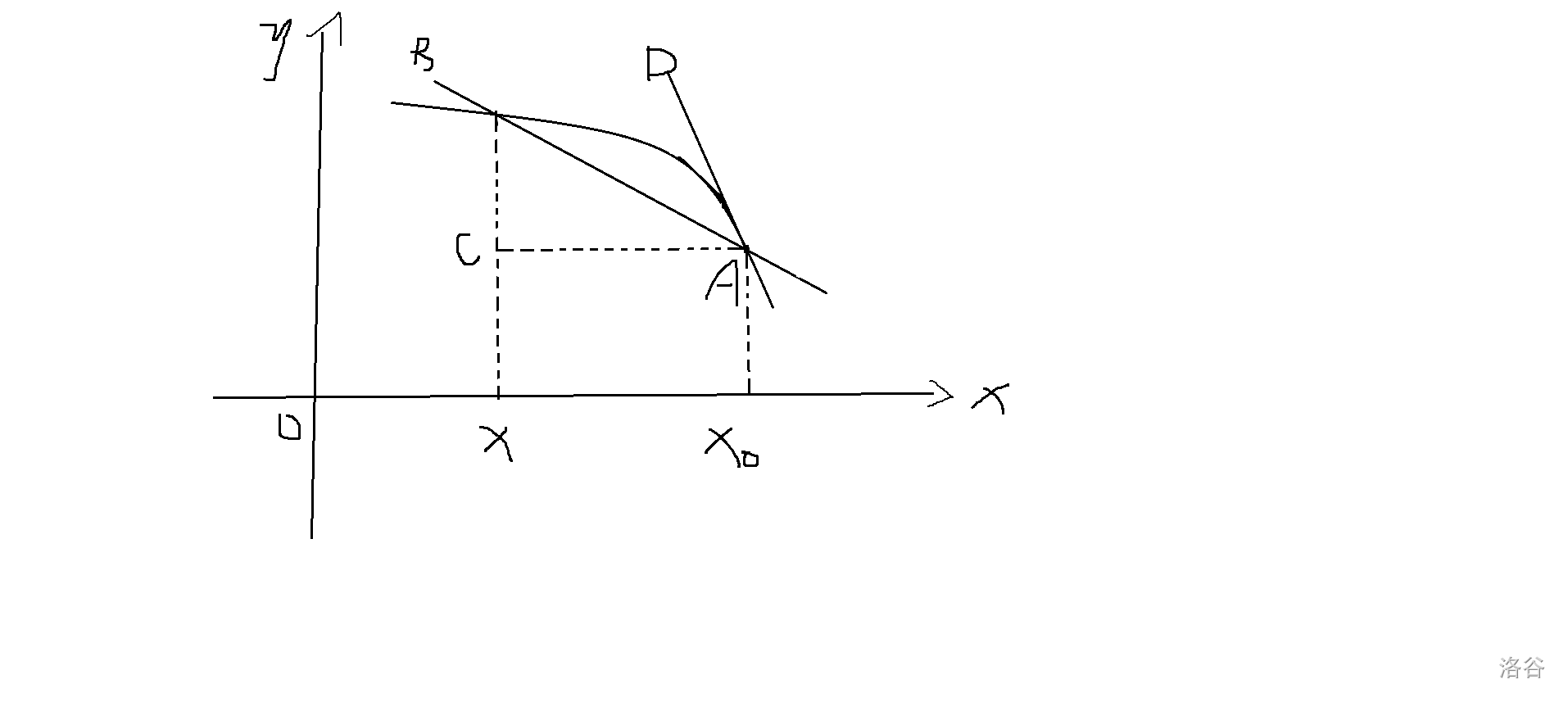
设函数 $y=f(x)$ 的图像如图所示（曲线）。

AB为过点 $A(x_0,f(x_0))$ 与 $B(x_0+\Delta x,f(x_0+\Delta x))$ 的一条割线。

由此可以得出，这条割线的斜率为 $\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\frac{\Delta y}{\Delta x}$。可知割线的斜率就是函数的平均变化率。

当点B沿曲线不断趋近于点A时，割线AB会绕着点A转动。当B与A重合时，AB会与AD重合。AD被称为函数 $y=f(x)$ 在点A处的切线，即 $\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=k_{AD}$。

由导数的意义可知，曲线 $y=f(x)$ 在点 $(x_0,f(x_0))$ 处的切线斜率为 $f^{\prime }(x_0)$。

可能会考的两种题型：

题型一 曲线在某点的切线

由于函数 $y=f(x)$ 在 $x=x_0$ 处的导数 $f^{\prime }(x_0)$ 的几何意义为曲线 $y=f(x)$ 在点 $(x_0,f(x_0))$ 处的切线的斜率，所以我们就可以通过以下步骤求得切线方程：

$(1)$ 求出 $y=f(x)$ 在 $x=x_0$ 处的导数，即$y=f(x)$ 在点 $(x_0,f(x_0))$ 处的切线的斜率。

$(2)$ 在知道切点坐标与斜率的条件下，因为切线一定为一条直线，所以用一次函数的求法即可求得切线方程。

注意：若$y=f(x)$ 在点 $(x_0,f(x_0))$ 处的切线平行于 $y$ 轴，那么切线方程为 $x=x_0$。

题型二 曲线过某点的切线

只需注意以下几点即可：

$(1)$ 曲线的切线不一定只与曲线有一个交点。

$(2)$ “曲线过某点的切线”与“曲线在某点的切线”是不同的概念。

$(3)$ “曲线在某点的切线”要么没有，要么只有一条。而“曲线过某点的切线”可能不止一条。

如何判断单调性：

如果函数 $y=f(x)$ 在 $x$ 的某个开区间内，总有 $f^{\prime }(x)>0$，则 $f(x)$ 在这个区间内是增函数。

如果函数 $y=f(x)$ 在 $x$ 的某个开区间内，总有 $f^{\prime }(x)<0$，则 $f(x)$ 在这个区间内是减函数。

用导数研究函数的极值：

已知函数 $y=f(x)$，设函数 $x_0$ 是定义域内任意一点。如果对 $x_0$ 附近的所有点 $x$，都有 $f(x)<f(x_0)$，则称函数 $f(x)$ 在 $x_0$ 处取最大值，并把 $x_0$ 称为函数 $f(x)$ 的一个极大值点。

求函数 $y=f(x)$ 在 $[a,b]$ 上的最大值与最小值的步骤如下：

$(1)$ 求函数 $y=f(x)$ 在 $(a,b)$ 内的极值；

$(2)$ 求函数 $y=f(x)$ 的极值，与端点处比较，就可以求出最大值与最小值。

一些题目

极限：

$1.$ 求 $\underset{x\to 3}{\lim }(4x^2-5x+1)$；

解析：

由于函数是连续的，所以极值就在 $x=3$ 时取到。

故答案为 $4\times 3^2-5\times 3+1=22$。

$2.$ 求 $\underset{x\to 1}{\lim }\frac{x^2+3x-1}{2x^4-5}$；

解析：

由于函数是连续的，所以极值就在 $x=1$ 时取到。

故答案为 $\frac{1^2+3\times 1-1}{2\times 1^4-5}=-1$。

$3.$ 求 $\underset{x\to \infty }{\lim }\frac{x^2+2x-3}{x^2-1}$；

解析：

直接取正无穷显然不可能，我们考虑对它进行化简。

原式 $=\underset{x\to \infty }{\lim }\frac{x+3}{x+1}$

$=1+\underset{x\to \infty }{\lim }\frac{2}{x+1}$

这里由于分离常数后 $1$ 为定值，所以可以直接提出来。

当 $x$ 趋于无穷时，$\frac{2}{x+1}$ 会趋近于 $0$，故答案为 $1$。

导数：

$1.$ 求函数 $f(x)=x^3-2x$ 在 $x=1$ 附近的平均变化率，在 $x=1$ 处的瞬时变化率与导数。

解析：

直接套公式即可。

平均变化率即为 $\frac{f(1+\Delta x)-f(1)}{\Delta x}$，将它展开爆解即可。答案为 $(\Delta x{)}^2+3(\Delta x)+1$。

瞬时变化率即为导数，答案即为 $f^{\prime }(1)=\underset{\Delta x\to 0}{\lim }\frac{f(1+\Delta x)-f(1)}{\Delta x}=(\Delta x{)}^2+3(\Delta x)+1=1$

$2.$ 函数 $y=a{x}^4+1$ 的图像与直线 $y=\frac{4}{3}x$ 相切，则 $a$ 的值为____。

解析：

先进行求导。

$y^{\prime }=4a{x}^3$，$y^{\prime }=\frac{4}{3}$。

那么我们设切点 $A(x_0,y_0)$。

我们就会得到两个方程：

$4a{x}_0^3=\frac{4}{3}$ 以及 $\frac{4}{3}{x}_0=a{x}_0^4+1$。

解得 $x_0=1$，$a=\frac{1}{3}$。

$3.$ 求函数 $y=\frac{x^3-2}{2(x-1{)}^2}$ 的极大值。

解析：

先求导，过程省略了。

$y^{\prime }=\frac{(x+1)(x-2{)}^2}{2(x-1{)}^3}$。

要求极值，所以我们令 $y^{\prime }=0$，解得 $x_1=-1,x_2=2$。

分类讨论 $x=-1$ 以及 $x=2$ 的情况即可。

$(1)x=-1$ 时，$f^{\prime }(x)$ 会变号，存在极值，经过计算可得 $x=-1,y=-\frac{3}{8}$。

$(2)x=2$ 时，$f^{\prime }(x)$ 不会变号，故不存在极值。

综上所述，极大值为 $y=-\frac{3}{8}$，在 $x=-1$ 时取到。

作者的后记

昨天刚第二次学导数，觉得自己学的不够牢固，于是突发奇想来写一篇学习笔记。

每一次看到别人学完新知识后都能记得很牢固，经过大佬们的推荐，听说学习笔记很有用，于是就来肝了一篇（其实也不算肝，用了4.5hrs,写了接近7k的文字量）。

当然，我觉得这篇学习笔记里面肯定是有很多不足的，所以还请大佬多多指教，谢谢观看！

2024.8.14 20:28