车载毫米波雷达信号处理中的模糊问题

说明

    在毫米波雷达的信号处理中，测距、测速、测角是我们关注的三个核心问题，以chirp形式的信号工作的车载毫米波雷达，其最大无模糊测量距离(仅从数据处理而非能量的角度考虑)受限于接收机的中频带宽和ADC的采样率，其最大无模糊测量速度受制于信号的PRF(或者说单天线所发射的chirp周期)，其最大无模糊测量角度受限于阵列中阵元之间的最小间距。

    很多时候在其它因素的限制下，前述几个参数的最大无模糊测量范围较小，没法满足实际应用的需求，此时我们就需要进行解模糊以将雷达对前述参数的测量范围扩大至我们所需求的范围。

    本博文试图探讨毫米波雷达信号处理中的这些模糊问题，理清楚其原理，并在博主所了解的范围内给出一些解决办法。本博文内容会随着后续积累的加深而不定期更新。

    本博文的仿真代码、实测数据和相应的数据处理代码见第七章的链接。

    第一章内容公式较多，用手机看有点乱码，建议使用电脑看。

Blog

20230303 博文第一次写作

文章架构

目录

说明

文章架构

一、车载毫米波雷达信号处理中的模糊问题综述

1.1 距离模糊问题

1.2 速度模糊问题

1.3 角度模糊问题

1.4 小结

二、距离模糊的解决办法

三、速度模糊的解决办法

3.1 速度解模糊的迫切性

3.2 速度解模糊方法介绍

3.2.1  基于中国剩余定理的速度解模糊算法

3.2.2 基于多普勒相偏补偿的速度解模糊算法

3.2.3 基于目标跟踪假设的速度解模糊算法

3.2.4 基于chirp时延与相位差值的速度解模糊方法

3.3 小结

四、角度模糊的解决办法

五、总结

六、参考资料

七、code & data

---

一、车载毫米波雷达信号处理中的模糊问题综述

    关于以chirp形式的信号工作的雷达测距、测速、测角的原理在此不做过多说明了，读者可以参考任何一篇与车载毫米波雷达相关的硕博毕业论文或者Ti的该文档：The fundamentals of millimeter wave radar sensors (Rev. A) (ti.com)。

1.1 距离模糊问题

    对于测距，从数据处理端来说，雷达的最远测量距离由以下公式决定：

    式中，c为光速，S为chirp信号的斜率，f与雷达接收机的中频带宽(对应接收链路上接收信号与本振信号混频后再低通滤波时该低通滤波器的截止频率，比如Ti的AWR2243其中频带宽是20MHz)以及ADC采样率fadc有关，我们假定雷达单个接收链路下是IQ两路采样的，则此时上述公式中f的取值为：

    我们认为频率高于的都被低通滤波器滤除掉了，于是进入到后端并被ADC采样的频率范围是[0    ]。

    对于 ≥  的情况，能采样得到的最大频率为，此时从数据处理的角度来说目标的最大检测距离就是：

    在距离FFT后，频率和距离是一一对应的关系，不会存在距离模糊的情况，此时我们想要提高最大测量距离可以通过降低chirp斜率S来实现。

    而对于 < 的情况，目标距离对应的频率处在-->范围内时，距离FFT后这段区间会被混叠到[0  -]区间里头去，此时确实会有所谓的距离模糊的情况发生：在频率为[0    -]范围内的检测结果，我们其实并不确定这些频率对应的目标距离是：

        -fadc ]

    还是：

    -fadc ]

    如下述视频所示：

测距模糊仿真结果

    此处仿真中，  = 20MHz，  = 15MHz，目标的频率从0Hz-->20MHz变化，可以看到，当检出的频率在[0  5MHz]时，目标位置对应的真实频率可以是[0  5MHz]或者是[15MHz 20MHz]

    博主也是写这篇博文时想到这个问题(这篇博文的初衷主要是讲清楚速度和角度的解模糊问题，因为距离模糊一般并不会出现)，除去仿真之外，我还拿Ti的级联板设计了实验并采集和分析了数据，这里一并给出实测数据下的结果：

测距模糊试验结果

    本次试验中，设置ADC采样率为5MHz，对应从数据处理的角度可达最远检测距离为6m，级联板AWR2243芯片的中频带宽是20MHz,该频率对应的距离是24m,实验过程中人拿着角反在雷达正前方来回走动，可以看到从第11帧开始目标从远处进入，从第17帧开始目标从近处远离，从第25帧开始消失在范围内。【但是：并没有在11帧之前以及25帧之后出现预想的情况：理论上应该在0-6m的范围内出现6m外的目标混叠进来的情况！】，很奇怪.. 目前我对此的解释是：Ti芯片的中频带宽会自动随着设置的ADC采样率的变化而变化(其低通滤波器的截止频率一定是小于等于ADC的采样率?这个问题先留在这里，后面如果知道了确定的解释再做补充。)

    以上描述了距离模糊的产生原因(条件)，但是如前所述，在车载毫米波雷达的实际应用中，测距模糊是极少出现(或者说是最容易解决的)，关于解决(或避免)的方法将在本博文的后续章节给出。应用于汽车的毫米波雷达在测距这个指标上我们更多的是从能量的角度来考虑雷达所能达到的最远检测距离，这与雷达方程以及雷达的系统设计有关，我后续会出一篇相关的博文讨论该问题。

1.2 速度模糊问题

    雷达的测速范围由以下公式决定：

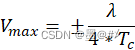
    式中，Tc为单天线前后发射的chirp之间的时间间隔。对该式的推导做简单说明：我们假定目标的速度为V，对于同一个发射天线，其前后发射的chirp信号我们采样并做距离FFT之后，该目标会出现在这两chirp的同一个距离索引和速度索引之下，但是它们之间有相位差：

    当我们得到相位差值∆φ后，便可以得到V:

    但是对于相位∆φ，它是有周期的（这个周期便是模糊的来源，两信号相差X°和两信号相差X±K*2pi，K取整数，是等价的），相位只有在±180°的范围内才是唯一的定值。从前式来看，相位差∆φ会随着V的增加而增加，在无模糊的范围内取为±180°时，对应的速度最大，该值即等于：

    有正负表示目标相对雷达的靠近和远离。当速度不在该区间内时，会混叠到该区间里头去，此时我们需要去做一些速度解模糊的操作以将之分辨出来。速度解模糊将是本博文重点讨论的内容。

1.3 角度模糊问题

    雷达的测角范围由下述公式决定：

    对于均匀阵列，式中d为阵列中相邻阵元之间的间距。同样对该式的来源做简单推导：在远场的条件下，对于同一个目标，相邻接收阵元之间目标的回波所传播的路程相差：

    式中，θ为目标相对雷达法向的夹角，该路程差∆D所产生的相位差为：

    联立上述两式可以得到角度θ为：

    同前述对速度的说明，对于相位∆φ，它是有周期的（这个周期也是模糊的来源，两信号相差X°和两信号相差X±K*2pi，K取整数，是等价的），相位只有在±180°的范围内才是唯一的定值。从前式来看，相位差∆φ会随着θ的增加而增加，在无模糊的范围内取为±180°时，对应的角度最大，该值即等于：

    有正负表示目标与雷达法线的夹角可以是偏左或者偏右。实际应用中我们一般取阵元之间的间距为0.5*λ，此时对应的最大无模糊测角范围在±90°，因为雷达不需要测量其背面的目标，所以阵元间隔取0.5个波长对应的最大无模糊测角范围±90°是合适的。角度模糊的来源在于：在一些应用中有时候因为阵列设计的考量，我们会将阵列阵元之间的间距扩大到大于0.5个波长，此时雷达的最大无模糊测角范围必然小于±90°，比如我们将间距设置为1个波长，此时最大无模糊测角范围为±30°，但是又想测量±90°范围内的目标，这个时候便会出现模糊的情况，比如下述仿真结果：

测角模糊说明

    此处仿真中，阵列为20个阵元间距为1个波长的均匀阵，对应最大无模糊测角范围在±30°内(对应视频图中的两条红色线)，目标的角度从-90°变化到90°，我们在±90°的区间内可以看到有至少两个波峰，或者说很多情况下目标没有在±30°范围内，但是该区间出现了波峰，这便是角度模糊的体现：我们不知道无模糊范围内的测角结果是否是目标的真实角度。

    关于角度解模糊其实我们需要关注两个问题：A、最大测角无模糊的区间是我们主动缩小的，但是我们需要得到更大角度区间的测角结果。B、我们只需要测量限定角度范围内的目标(比如长距雷达我们只需要测量±9°范围的目标)，但是如果天线在该角度范围外的能量控制得不好，导致该角度范围外的目标混叠进我们关注的角度范围内并导致虚警的情况发生。

    第二个问题其实也很有意思，不过这种情况我们应该可以寻求优化天线设计(把天线的水平向波束角尽量缩小，以使得大角度范围下的目标因为能量弱而检测不到)、以及长距下我们尽量不去考虑近处的目标：一般长距雷达都有所谓的短距模式，短距模式用于负责测量宽角度范围的近处目标，而长距模式我们可以直接忽略掉近距范围内的目标而不去管该范围内是否是角度混叠进来的。此外，对于远处的目标，因为小角度下在远处可以覆盖很宽的水平向距离(比如100m的纵向距离下，±9°对应的横向宽度可达约32m)，所以远处其实一般也不会有设计的测角范围外的目标混叠进来的情况发生。

    后文在使用角度解模糊算法解决角度模糊问题的讨论中，我们重点关注第一种情况。

1.4 小结

    本章内容对毫米波雷达测距、测速、测角的模糊问题做了清晰的描述。测距模糊一般来说都是可以避免的，后文的讨论主要谈谈如何避免测距模糊；测速的模糊大多数情况下是需要解决的，特别当发射的通道数增加时，最大无模糊的测速范围会急剧下降（不同的发射模式以及关于测速模糊简单讨论可以参考我之前的博文：车载毫米波雷达MIMO阵列的天线发射问题_墨@#≯的博客-CSDN博客），速度解模糊将是后文的重点；测角模糊更多的是我们在设计阵列时不得已而主动为之的一种情况，后文也将讨论关于角度解模糊的方法。

二、距离模糊的解决办法

    通过上一章的分析我们可以知道，距离模糊的成因在于ADC的采样率小于中频带宽(或者说混频后低通滤波器的截止频率)，Ti在其芯片手册中都只给出中频带宽是多少的说明，该带宽的高通滤波器的截止频率是可以调节的，但是并没有对低通滤波器的截止频率做可调节的说明。如果芯片内部的该截止频率可以随着设置的ADC的采样率自动发生变化并有：Fif≤fadc,那距离混叠这个问题就不会存在。但是应该不是这样(可如果不是这样该如何解释上面第一章的实测结果呢？这个问题暂留存，后文的讨论是在不支持这里的假设的前提下所做出的：也即其中频带宽对应的低通滤波器的截止频率不变)。

    距离模糊问题我这里讨论如何去避免这个问题产生。很直接的一点是：在做系统参数设计时，我们可以将ADC的采样率设置得很高，以至盖过中频带宽的大小，此时自然不会有混叠的发生（ADC采样率的增加可以让我们在相同的时间内采集更多的点，这对信号处理也是有益的），因为对于距离的设计(从数据处理端)，我们可调节的参数从前述距离公式来看还包括chirp斜率，在同样距离的要求下，提高采样率后我们可以通过减小chirp斜率来满足参数设计的要求。

    此外，其实很多情况下即便ADC的采样率小于中频带宽，当fadc对应的距离足够大时，可能从能量的角度来看，雷达此时已经无法检测到那么远距离下的目标了，此时是否有混叠的产生其实没有了意义。

    在做雷达的系统设计时，我们更多的是从能量的角度来考虑最远检测距离这个指标，在最远检测距离这个参数的要求下，去分配天线增益、接收链路增益等各项指标，再从数据处理端来设计收发参数，一个合格的雷达产品在我们所设计的收发参数下应该满足雷达从数据处理端得到的Rmax_process（当fadc<Fif时，该Rmax_process对应fadc,当fadc>Fif时，该Rmax_process对应Fif）大于等于从能量的角度可以到的Rmax_power。在这样的前提下，当fadc>Fif时自然不会有混叠，当fadc<Fif时，其实此时大于等于Rmax_process的目标雷达从能量的角度已经看不到了，混叠以及混叠导致的虚警增加的讨论也就没有了意义。

三、速度模糊的解决办法

3.1 速度解模糊的迫切性

    速度模糊的解决是本博文讨论的重点。回到前述公式：

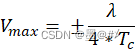
    从该式可以看到，因为λ是确定的，当单天线前后所发射的chirp周期Tc确定时，雷达的最大无模糊测速范围也就确定了。我们考虑TDM-MIMO的发射模式来直观地评估一下该最大无模糊测速范围的大小，Ti的芯片大多是3T4R的通道数，就以3个发射通道为例，假定TDM下前后chirp的发射间隔为30微秒(该值算是很小的了)，则Tc = 30*3 = 90微秒，λ取77GHz对应的0.0039m，此时Vmax = ±10.83m/s或39kph。该值与一般来说来车载雷达产品的测速范围要求：≥±200kph差距极大。这里的评估针对的30微秒的发射间隔是很保守的一个值，且当通道数增加时该值就更大了，所以对于最大无模糊测速范围的拓展是必须要解决的一个问题。

3.2 速度解模糊方法介绍

    速度解模糊方法很多，以下内容主要基于Ti的文档（参考资料1）以及加特兰的baseband说明(参考资料2)。

3.2.1  基于中国剩余定理的速度解模糊算法

    这个算法强调了是基于中国剩余定理的，那么有必要了解什么是中国剩余定理：如果一个自然数对一组互质的因子分别取余数，那么在知道余数和互质因子的情况下，一定可以计算出原始的自然数。后面在介绍具体算法时再对照这句话进行理解。

    首先需要明确的一个前提（该前提是通用的，同样适用于后续给出的算法）：假定目标的真实速度为Vr，在我们的无模糊测速范围(±Vmax)内得到该目标的测量速度为Vm，则Vm与Vr以及Vmax之间满足如下关系：

Vm = Vr mod Vmax   或者可以写成： Vr = Vm + 2*K*Vmax  K为整数。

    在这样的一个前提下，我们便可以结合前面的中国剩余定理来设计解速度模糊的方法：试想，如果我们设计两套发射参数(可以简单理解成两帧，对应Fast chirp帧和Slow chirp帧)，这两套参数只有Tc有差异(我们可以通过更改chirp之间的时间延迟来很容易地实现)，其它的包括chirp斜率、采样率、采样点数等等都没有差别。如下图所示：

以前后快慢帧发射的形式来解速度模糊示意图

    则此时依据前述最大无模糊测速范围的公式，必然可以得到两个不同的最大无模糊测速范围，我们假定这两种快慢帧下的最大无模糊测速范围为±Vmax1和±Vmax2。对于同一个目标，在前后两帧下速度大小可以认为是不变的(因为时间间隔很小，一般是ms量级，所以包括目标的速度以及目标相对雷达的距离都认为是不变的。)，我们假定其真实速度为Vr，此时我们可以得到两个测量速度：

Vm1 = Vr mod Vmax1     Vm2 = Vr mod Vmax2

    对应到前面中国剩余定理的那段话，Vm1和Vm2就是所谓的余数，Vmax1和Vmax2就是互质因子(互质我们可以通过调节chirp之间的时间延迟很容易实现)。基于这四个值我们就可以求得唯一的Vr。

    具体怎么基于这四个数去求解，这里不做讨论，因为我们实际使用时并不会用到，Ti给的说法是：“中国剩余定理通过余数求解原始自然数的过程是通过求解方程来实现的，在 DSP 软件上很难实现。”我们后续算法用到中国剩余定理的点其实是其结论：因子互质，知道因子和余数便一定可以计算出原始的自然数。且这个自然数必然是唯一的。得到该自然数我们不能用计算(解方程)的方法，但是可以尝试用其它的方法！Ti给的方法可以用文字解释如下：

【算法原理文字描述】：

    首先我们可以得到目标在Fast chirp（对应Tc较小的那一帧）上的能量值amplitude1，然后我们对物体的实际速度Vr是否超过Fast chirp的最大检测速度Vmax1做出假设：

Vr_hypothesis =  Vm1 ± 2*N*Vmax1，  N = 0、1、2…

   并依照这个假设的Vr_hypothesis推算出在Slow chirp上对应的Doppler索引(前面已经说明了目标在这两帧下的距离和速度一样，所以这里我们是在同一个距离门下的速度维度去找Doppler索引)，或者说对应的Vm2,计算方法就是前面的公式：Vm2 = Vr_hypothesis mod Vmax2，得到了Vm2也就得到了其Doppler索引，随后基于Slow chirp这个Doppler索引上的目标反射能量值amplitude2是否等于前述的能量值amplitude1(或者说和前述能量值之间的差距小于某个阈值)来判断这个假设是否成立，我们从中找到最接近的能量值对应的假设，并认可该假设对应的是真实速度，从而得到该假设对应的N，并进而得到Vr。

    可以看到，我们评价对应与否的基准是目标两帧下对应的目标能量值，这是一个很好的凭借,我觉得这也是这个算法出彩的地方：我们需要结合实际应用去寻找并抓住那些不变的东西来为自己所用。

【算法伪代码与流程】

 【算法的补充说明】

   该算法需要注意的点是：这里的速度解模糊算法并不能把最大无模糊测速范围无限制地扩大(不过其实我们也没必要无限扩大，比如我们从3.1节中假设的39kph扩展到200Kph，扩展至原来的5倍即可，对应到前面对N的假设，即为该N最大取到4。当然，速度更高的目标也可能混叠进去，但是实际路上相对速度超过200kph的目标情况基本可以忽略不记吧？)。不能无限制扩大是指从原理上对能解到的最大无模糊测速范围的限制，该方法能解到的最大无模糊速度值是Vmax1*Vmax2，这是从中国剩余定理出发得到的，因为如果超过该值，那么我们通过这两因子以及对应的余数其实可以得到多个所谓的自然数了（比如我们设其为Vs，在超过Vmax1*Vmax2时，该值可以是：Vs+k*(Vmax1*Vmax2)，K为整数，当然，在小于Vmax1*Vmax2里只有一个，），这是在参数设计过程中需要注意的。

    实际应用中，我们其实可以很容易避免说Vmax1*Vmax2仍然没法满足最大无模糊测速范围的要求。因为在以设计前后帧这样的方式来解速度模糊时，我们可以对所谓的fast chirp只使用其中一个发射通道发射，而slow chirp正常发射并作为雷达检测目标之用。比如3.1中所设想的3T4R的情况，我们Fast chirp帧下只做1T4R，此时该Fast chirp下的最大无模糊测速范围可以至少(我们还可以缩减Tc使得其Vmax增加并与3T下的Vmax互质)增加到39*3 = 117Kph，此时以1T4R和3T4R理论可解的无模糊测速范围可以到4563Kph。

    另外还需要注意的一点是：我们是以两种模式下、同一个距离门下的、多普勒维度找到的索引对应的能量值进行比较。严格来说还是有一点问题的：比如出现该距离门下有多个目标，而不巧的是我们分析的这个目标混叠后在多普勒维度的索引刚好在其它目标的位置上(或者临近其它目标，此时其它目标泄露的能量也会影响我们的判断)，这必然就会导致能量的“失真”。当然，实际应用中这种情况必然是极少出现的，此外我们可以通过增加距离和速度的分辨率来减少这些情况的发生。

3.2.2 基于多普勒相偏补偿的速度解模糊算法

A、关于多普勒相偏补偿

    理解这种算法我们首先需要弄清楚什么是多普勒相偏补偿【其实这个概念应该是隶属于DOA估计里，我在之前的博文：车载毫米波雷达MIMO阵列的天线发射问题_墨@#≯的博客-CSDN博客，第二章TDMA部分有过简单说明】。MIMO(多发多收)这种体制已经被广泛地应用于雷达的各项应用，车载毫米波雷达也是，我们可以通过设计阵列的排布使得MIMO下获得更大的阵列孔径并进而获得更高的角度分辨率，能开始看解模糊算法的你相信对MIMO这个简单的概念已经很熟悉了，这里不做展开说明。

    这里以2T4R的均匀阵对多普勒相偏这个概念做更详细一点的说明(后续的算法说明也基于此)：

TDM下多普勒相偏的产生示意图

    发射天线间距两个波长，接收阵列为间距0.5个波长的均匀阵，TDM下会产生8个间距为0.5个波长的均匀阵列。从其排布的角度来看，这8个阵元之间相邻两个阵元之间的相位差为：

    我们以第一个为基准，则理想情况下这八个阵元之间的相位关系应该是：

[0  w  2w  3w  4w  5w  6w  7w ]

    但是不难理解的是：在目标有速度Vr的前提下，因为天线是分时发射的，在这个时间差Tc(这里定义为前后两个天线发射的时间间隔)和Vr的共同作用下(目标有微弱的运动，而相位对微弱的运动是极其敏感的)，必然会导致第二次发射的天线对应的四个接收通道相较于第一次发射对应的四个接收通道有一个额外的相位差，且这个相位差等于：

    也即，相较于理想的情况，这8个阵元的实际相位关系应该是：

[0  w  2w  3w  4w+∆φ  5w+∆φ  6w+∆φ  7w+∆φ]

    这多出来的∆φ是会影响我们测角的，所以我们在实际测角之前，需要将该∆φ补偿掉，所谓的补偿就是把后面四个通道的相位都减去∆φ，这便是多普勒相偏补偿。不难推广的是：如果有更多的发射天线以TDM的方式发射，那么对应的相位应该是：

[0 w .. 4w+∆φ 5w+∆φ .. 8w+2*∆φ 9w+2*∆φ … 4*(K-1)*w+(K-1)* ∆φ]

    我们以第一个发射天线为基准，后面发射天线相较于第一个发射天线的时间延迟会发生变化(0—-Tc—-2Tc---(K-1)Tc)。

    从前述相位差∆φ的公式可以看出，该补尝值计算得准确与否取决于我们求得的Vr是否准确。所以我们是在测速的基础之上去做相位补偿，这里就与我们的测速模糊以及解模糊关联上了。

B、基于多普勒相偏补偿的速度解模糊方法

    明白了前述多普勒相偏补偿的概念，这里的速度解模糊方法就很好理解了。

【算法的文字描述】

    我们需要进行速度解模糊就说明我们不确定我们测量得到的速度Vm是否是目标的真实速度，同样根据上一节中国剩余定理算法中说明，Vm与目标真实速度Vr之间满足关系Vr = Vm ± N*2*Vmax。于是我们可以基于该公式假设不同的实际速度Vr_hypothesis，并用这些假设的速度得到对应的相位补偿值来做相位的补偿，再进行测角。该算法的依据是：只有当我们补偿的相位是真实的相位值时，我们做完角度FFT后得到得才是FFT峰值，我们通过比较不同假设速度下补偿后的测角结果来评估哪个假设(对应的FFT峰值是最大的，或者Ti取的是测角后的各个点的幅度平方和最大者)是我们所认可的，并将该假设的速度作为目标的真实速度从而完成速度解模糊。

【算法的伪代码】

 【算法的补充说明】

    本方法相较于前面基于中国剩余定理的算法的优势在于不需要另外发射一帧信号。但是本算法的缺点同样很明显：The algorithm works well when the single target occurs in range/Doppler bin. However it can fail with multiple targets in the same range/Doppler bin. It also fails with multiple targets at the same range and different velocities wrapped to the same Doppler bin. 这段话同样适用于上一节的速度解模糊算法，我已经在前面做了说明，而本节的算法因为牵扯到相位，对于同一个距离门乃至同一个距离和速度门下有多个目标的情况就更加敏感了，同样，为解决(或减少该情况的发生)这个问题我们可以通过增加这两个维度的分辨率来实现。

    此外，这种算法在我目前的理解看来，其最大的缺点在于速度扩展的范围很小！Ti在其文档中（参考资料1）的说明并不严谨和通透。但是从其给的上面的伪代码可以看到一些信息，首先说结论：这种算法对无模糊测速范围的扩大与发射的天线数量有关，具体到2T4R其实只能往外扩大2*Vmax。

    再来说原因，把这几个公式摆出来就明白了，最大无模糊测速范围：

    本小节前述定义Tc为前后两chirp之间的时间间隔，这里有两个发射通道，上述公式中的时间应该对应单个发射天线发射的chirp间隔为2*Tc。速度引起的相位差值：

    真实速度Vr与测量速度Vm之间的关系：

Vr= Vm ±N*2*Vmax    N取整数(0、1、2 …)

    我们联立上述三个式子可以得到：

    从上式可以看到，我们将速度进行N*2*Vmax地扩大时，补偿到后续发射天线的相位其实和Vm对应的补偿相位之间差pi的整数倍，N = 1时对应pi，N = 2时对应就是2*pi了，补偿(）与补偿是没有区别的，我们得到的测角结果将会是一模一样的！如下图仿真结果所示：

 8阵元均匀阵中不同阵元位置相位的不一致对测角的影响1

    所以我们不能将目标的速度进行N*2*Vmax地扩大，具体到这里分析的2T4R的情况，我们只能将N取为0或1，所以可以看到Ti给的前述伪代码中，X’’直接就是X’取复共轭conj即可(相位翻转pi)。N取为1时对应相位变化为：

    此时在∆φr和∆φm下补偿的结果将是不同的：

8阵元均匀阵中不同阵元位置相位的不一致对测角的影响2

    如果我们将后四个阵元加30°相位对应的曲线作为正确补偿后的结果，可以看到如果我们补偿了（30°+180°）则其测角结果的峰值明显比前者低。

    综上解释了前面说的结论：这种算法对无模糊测速范围的扩大与发射的天线数量有关。更一般地，对于Ntx个发射天线的情况，不同模糊倍数下需要补偿的相位关系满足：

    读者可以基于该公式和上面的解释，去分析使用该方法在不同发射天线数量下所能往外拓展的速度范围。

3.2.3 基于目标跟踪假设的速度解模糊算法

    前面的两种方法是从信号处理的角度来扩展速度的无模糊范围，这里基于目标跟踪假设的算法顾名思义是基于更后端的数据处理(跟踪算法)来实现，如果对跟踪算法有了解，这部分内容其实很容易理解。

【算法原理的文字描述】

    我们在做目标跟踪时，会为每个跟踪到的目标分配一条航迹tracker，跟踪算法分为两个部分：一是航迹关联；二是滤波。所谓的关联是指将原有的航迹与本帧检测到的目标点云进行匹配，基于目标跟踪假设的速度扩展算法，是在做关联的时候对本帧检测到的目标速度Vm首先进行多种假设(Vr_hypothesis = Vm±2*N*Vmax),随后在关联时对这几种不同的速度假设都进行处理，根据打分的结果(Scoring，也就是和tracker历史信息匹配的程度【也即我们是认可原有tracker的速度信息的】)来判断一个假设是否成立，对于成立的假设认为它是一个合理的速度值，带入对应的tracker进行后续的滤波处理。这样通过目标跟踪算法判断了目标的合理速度值，解决了目标检测时最大检测速度不够的问题。

【算法的补充说明】

    这确实是一种很有意思的思路，往后有机会我会尝试实践一下。这里方法的解模糊范围应该可以做到很大，但是也有风险，因为我们做关联时是对每个track和每个检测到的点云都做比较，如果我们关联时给到速度的权值过大会导致产生很奇怪的匹配结果（前面两种算法也只是在同一个距离门的目标会影响到我们的判断，这里所有的点云都会影响）。

3.2.4 基于chirp时延与相位差值的速度解模糊方法

     本小节的方法也与目标速度Vr与前后发射的chirp之间的时延Tc有关，读者可以与前述基于多普勒相偏补偿的速度解模糊方法做对比以加深理解。

    本方法在所有的发射天线中事先选择一个发射天线，并在每个loop的正常发射前，用这个事先选择的发射天线增加一次发射，且该增加的发射与后续正常发射的区别只在于周期不一样，如下图所示：

 基于chirp时延与相位差值的速度解模糊方法的发射机制

发射时序图

    在前述这样的发射机制下，3T4R之下其实我们可以得到16个接收数据矩阵。且这16个数据矩阵速度维度的采样间隔都是一样的：(Tr*4+a),我们不妨将这些矩阵命名为ADCdata_mat1-->ADCdata_mat16（分别按照顺序对应从Tx0对应的四个接收通道到Tx2对应的四个接收通道），不过具体到这里的速度解模糊算法，我们取Tx0对应的ADCdata_mat1和ADCdata_mat5来分析，不难理解的是，这两个矩阵对应(距离和速度索引值相同)的每个点之间的时间差为(Tr+a)。对这两个矩阵做2D-FFT，得到矩阵RDmat1和RDmat5，因为这两个矩阵距离和速度维度的采样间隔和采样点数都一样，所以对于一个目标，其在这两个矩阵中的索引(Rindex,Vindex)也必然一样。注意到这两个矩阵对应的阵元位置是一样，所以这两个矩阵之间对应的(距离和速度索引值一样的点)所有点都没有因为目标角度和阵元位置产生的相位差，这两矩阵对应的点之间只有因为目标速度Vr和时间延迟（Tr+a）而导致的相位差(不过实际该相位差值还包括：热噪、干扰、以及其它有可能处在同一距离和速度门下的目标带来的相位差值，这部分相位差值这里用φn代表)：

    这两个矩阵每个点的相位值我们是可以直接得到的:

    那么我们就可以基于得到的相位差值∆φ、时间延迟(Tr+a)、实测速度Vm、设置不同的模糊倍数K并得到对应实际速度Vr = Vm + 2*K*Vmax（需要注意的是这里的Vmax = λ/（4*（Tr*4+a））。），进行拟合和比较以找到最合适的K进而得到我们解模糊后的Vr。【加特兰在其basband中有另外的求K的方法】

     这种方法也是有局限性的，并不能无限地扩展无模糊测速范围，因为相位是有周期的。该方法能拓展的最大倍数K和时延a以及Tr之间有如下关系：

K = (Td/(GCD(Td,Tr+a)))

     Td为速度维度的采样周期，对应上面3T4R的示例为：Td = Tr*(3+1)+a，GCD为求解两数的最大公约数。

    本方法的原理我上面大致讲明白了，关于更细节的包括K的求解，建议读者参考给出的参考文档。

3.3 小结

    本章内容首先通过假设的实例直观地阐述了速度解模糊的必要性和迫切性，随后介绍了博主本人现阶段所了解到的几种经典的速度解模糊方法，详尽地分析了其原理，并给出了每个算法局限性的探讨。当然，针对速度模糊这个问题，解决的方法还有很多，如果在往后的学习和工作中有了解到了其它有意思的算法，我再做丰富。

四、角度模糊的解决办法

    角度解模糊部分我们讨论：最大测角无模糊的区间是我们主动缩小的(为什么要这样做？：在相同阵元数目的条件下，可以获得更高的角度分辨率和测角精度)，但是我们需要得到更大角度区间的测角结果。

     网上关于角度解模糊的探讨很少，找的一些知网上的论文问题很多从原理到结论并不严谨，比如参考资料3。这个话题截止目前我研究的并不多，没法做详尽和严谨的叙述，这里给出我找到的一些资料【参考资料4、5】和现阶段研究得到的一些结论：

【1】角度的混叠和速度的混叠不一样，速度是线性的，角度不是，sin(θ)才是线性的，不过角度模糊虽然不是线性混叠的，但也是有规律的，且我们感兴趣的角度范围就那么些(最多到±90°)，所以解模糊倍数不会很大。

【2】如果目标角度超过测角无模糊范围，其混叠到测角无模糊范围内只有一个目标(波峰)，由此可以得到的一点信息是(此时不考虑目标角度间隔低于角分辨率的情况)：FFT或DBF测角后±θmax里头有多少波峰，就对应有多少个目标！我们只是不清楚这些目标是否是从外边混叠过来的。（不过也有特殊情况：测角范围外的目标混叠进来的角度刚好等于在无模糊范围内另一个目标的角度）

【3】对应上面的特殊情况：如果测角无模糊范围内某个目标的角度刚好等于另外一个角度的模糊后混叠进来的角度，此时这两个目标会完全混在一起。这两个目标在±90°范围内全部的波峰都会重叠！这就会很麻烦了。

【4】阵列间距和单个目标的峰值点的个数是有关系的：一个目标在±90°范围内存在的波峰数量 = 阵元间距 / (0.5*波长)

    以及做的一些仿真结果(观察现象)：

不同阵列孔径下的测角结果

    因为想早点把这篇博文发出来，本章内容目前只能如此，我后面会补充本章内容。

五、总结

    本博文探讨了车载毫米波雷达信号处理中的测距、测速、测角模糊问题。首先理清楚了其各自内在的原理，随后在博主所了解的范围内给出一些针对这几个问题的解决办法。本博文内容会随着后续积累的加深而不定期更新。

六、参考资料

1、基于AWR1642 汽车雷达的速度扩展算法研究 (ti.com.cn)

2、Alps radar baseband user guide  加特兰微电子 - Alps (calterah.com)

3、郑建超. 77G汽车防撞雷达角度测量算法研究[J]. 火控雷达技术, 2021, 50(2):4.

4、高分辨率无模糊雷达，CN 115047457A，发明专利，申请人为：通用汽车环球科技运作有限责任公司，这篇专利公布日是20220913

5、一种天线阵列的解角度模糊方法、装置及存储介质，CN 114167378A，发明专利，申请人为：福瑞泰克智能系统有限公司，这篇专利公布日是20220311

七、code & data

    需要两个积分，链接如下：

车载毫米波雷达信号处理中的模糊问题相对应的代码和数据-智慧交通文档类资源-CSDN文库