相似性用来衡量两个变量的相似程度。对于两个样本x(i),x(j)之间的相似性度量至少应满足以下要求:
1)应为非负值;
2)样本本身的相似性度量最大;
3)度量应满足对称性
常用的相似性度量可以分为距离函数和和系数函数两类。对于如何选择,可以参考以下几点:所选的相似性尺度在实际应用中应有明确的意义;根据原始的数据性质选择适当的变换方法,在根据不同的变换方法选择不同的距离或者相似系数;适当考虑计算量的大小。
对于两个N维的向量x1,x2,常用的相似性度量有:
1、欧氏距离:多维坐标下的距离,常见的有二维坐标、三维坐标。
2、曼哈顿距离
出租车距离或者曼哈顿距离表示两个点在标准坐标系下的绝对轴距总和。
3、切比雪夫距离
两个点之间的距离定义式其各个坐标数值差的最大值。
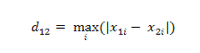
4、明可夫斯基距离
它是一组距离的定义式,当参数p取不同值时,可以化为其他距离表达式。
5、标准化欧氏距离
由于各维度的分布可能不一样,先将数据做一下标准化,其中s为样本各维度的标准差。
6、马氏距离
S为协方差矩阵。若S为单位矩阵,则马氏距离为欧氏距离;若为对角矩阵,则变为标准化欧氏距离。马氏距离对量纲不敏感,排除了变量间的相关性干扰。
7、夹角余弦
8、汉明距离
汉明距离定义的是一个字符串变换到另一个字符串所需的最小替换次数。
9、杰卡德相似系数
两个集合A和B的交集元素在A、B的并集中所占的比例,衡量两个集合相似的程度。
10、杰卡德距离
两个集合不同元素占所有元素的比例,衡量两个集合的区分度。
11、相关系数

12、相关距离
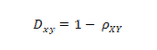
13、兰氏距离
对量纲不敏感,受奇异值的影响小,适合高度偏倚的数据,但假定变量间相互独立,没有相关性。
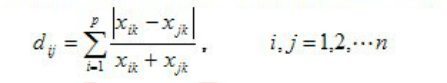
14、斜交空间距离
m为样本个数,p为样本的维数,r(ij)为变量间的相关系数。
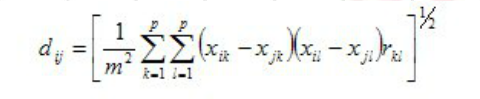
15、指数相似系数
不受量纲的影响,其中S为标准差。
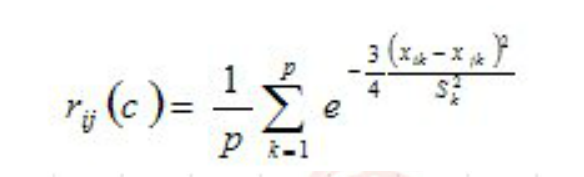
16、非参数化相似度(最大最小相似度)
x(ij)均大于0。
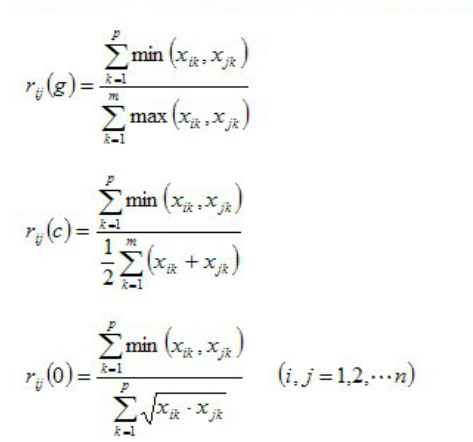








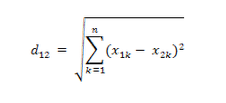
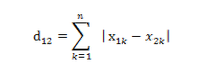
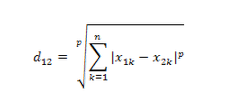

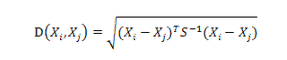
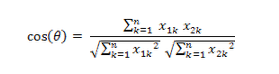
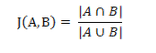

















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








