多层感知机:MLP
多层感知机由感知机推广而来,最主要的特点是有多个神经元层,因此也叫深度神经网络(DNN: Deep Neural Networks)。
感知机:PLA
多层感知机是由感知机推广而来,感知机学习算法(PLA: Perceptron Learning Algorithm)用神经元的结构进行描述的话就是一个单独的。
感知机的神经网络表示如下:
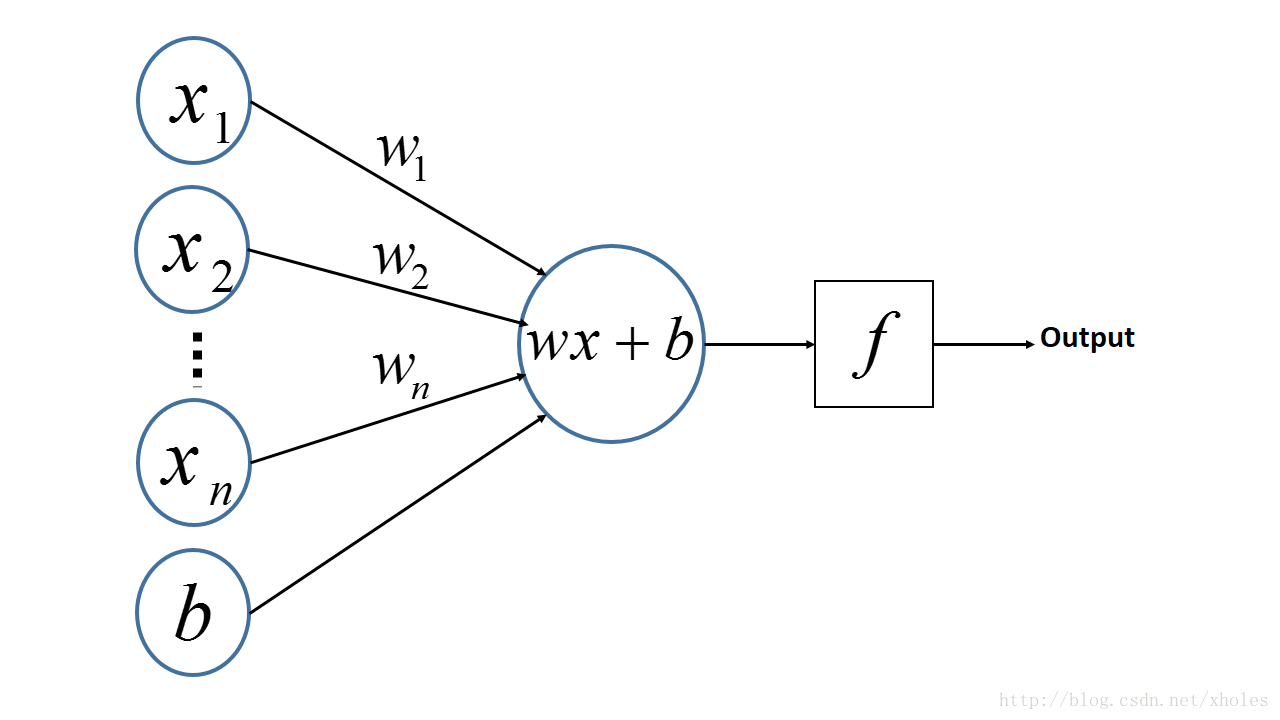
u=∑i=1nwixi+by=sign(u)={+1,u>0−1,u≤0
从上述内容更可以看出,PLA是一个线性的二分类器,但不能对非线性的数据并不能进行有效的分类。因此便有了对网络层次的加深,理论上,多层网络可以模拟任何复杂的函数。
多层感知机:MLP
多层感知机的一个重要特点就是多层,我们将第一层称之为输入层,最后一层称之有输出层,中间的层称之为隐层。MLP并没有规定隐层的数量,因此可以根据各自的需求选择合适的隐层层数。且对于输出层神经元的个数也没有限制。
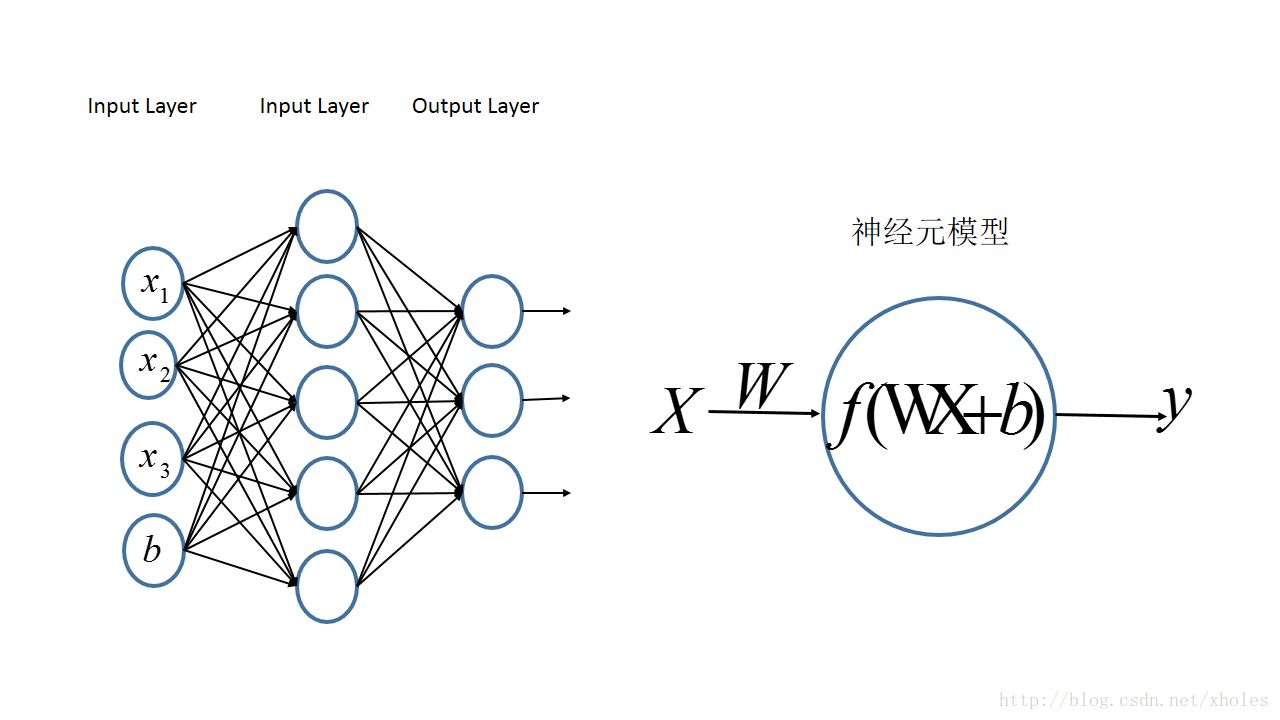
MLP神经网络结构模型如下,本文中只涉及了一个隐层,输入只有三个变量
[x1,x2,x3]
和一个偏置量
b
,输出层有三个神经元。相比于感知机算法中的神经元模型对其进行了集成。
前向传播
前向传播指的是信息从第一层逐渐地向高层进行传递的过程。以下图为例来进行前向传播的过程的分析。
假设第一层为输入层,输入的信息为[x1,x2,x3]。对于层
l
,用Ll表示该层的所有神经元,其输出为
yl
,其中第
j
个节点的输出为y(j)l,该节点的输入为
u(j)l
,连接第
l
层与第(l−1)层的权重矩阵为
Wl
,上一层(第
l−1
层)的第
i
个节点到第l层第
j
个节点的权重为w(ji)l。
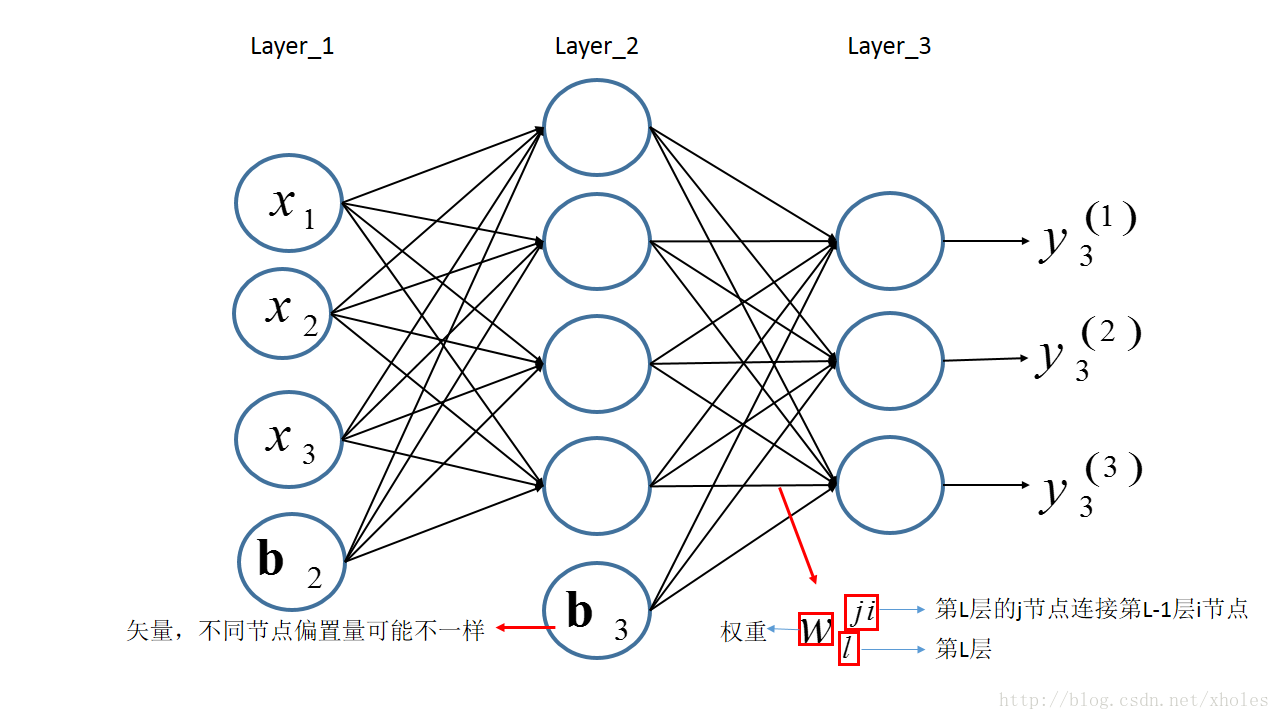
结合之前定义的字母标记,对于第二层的三个神经元的输出则有:
y(1)2=f(u(1)2)=f(∑i=1nw1i2xi+b(1)2)=f(w(11)2x1+w(12)2x2+w(13)2x3+b(1)2)y(2)2=f(u(2)2)=f(∑i=1nw2i2xi+b(2)2)=f(w(21)2x1+w(22)2x2+w(23)2x3+b(2)2)y(3)2=f(u(3)2)=f(∑i=1nw3i2xi+b(3)2)=f(w(31)2x1+w(32)2x2+w(33)2x3+b(3)2)
将上述的式子转换为矩阵表达式:
y2=⎡⎣⎢⎢⎢y(1)2y(2)2y(3)2⎤⎦⎥⎥⎥=f⎛⎝⎜⎜⎜⎡⎣⎢⎢w112w212w312w122w222w322w132w232w332⎤⎦⎥⎥⎡⎣⎢x1x2x3⎤⎦⎥+⎡⎣⎢⎢⎢b(1)2b(2)2b(3)2⎤⎦⎥⎥⎥⎞⎠⎟⎟⎟=f(W2X+b2)
将第二层的前向传播计算过程推广到网络中的任意一层,则:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪y(j)l=f(u(j)l)u(j)l=∑i∈Ll−1w(ji)ly(i)l−1+b(j)lyl=f(ul)=f(Wlyl−1+bl)
其中
f(⋅)
为激活函数,
b(j)l
为第
l
层第
j个节点的偏置。
反向传播
基本的模型搭建完成后的,训练的时候所做的就是完成模型参数的更新。由于存在多层的网络结构,因此无法直接对中间的隐层利用损失来进行参数更新,但可以利用损失从顶层到底层的反向传播来进行参数的估计。(约定:小写字母—标量,加粗小写字母—向量,大写字母—矩阵)
假设多层感知机用于分类,在输出层有多个神经元,每个神经元对应一个标签。输入样本为
x=[x1,x2,⋯,xn]
,其标签为
t
;
对于层
l
,用Ll表示该层的所有神经元,其输出为
yl
,其中第
j
个节点的输出为y(j)l,该节点的输入为
u(j)l
,连接第
l
层与第(l−1)层的权重矩阵为
Wl
,上一层(第
l−1
层)的第
i
个节点到第l层第
j
个节点的权重为w(ji)l。
对于网络的最后一层第
k
层——输出层,现在定义损失函数:
E=12∑j∈Lk(t(j)−y(j)k)2
为了极小化损失函数,通过梯度下降来进行推导:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∂E∂w(ji)l∂E∂b(j)l=∂E∂y(j)l∂y(j)l∂w(ji)l=∂E∂y(j)l∂y(j)l∂u(j)l∂u(j)l∂w(ji)l=∂E∂y(j)l∂y(j)l∂b(j)l=∂E∂y(j)l∂y(j)l∂u(j)l∂u(j)l∂b(j)l
在上式子中,根据之前的定义,很容易得到:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∂y(j)l∂u(j)l∂u(j)l∂w(ji)l∂u(j)l∂b(j)l=f′(u(j)l)=y(i)l−1=1
那么则有:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∂E∂w(ji)l∂E∂b(j)l=∂E∂y(j)l∂y(j)l∂u(j)l∂u(j)l∂w(ji)l=∂E∂y(j)lf′(u(j)l)y(i)l−1=∂E∂y(j)l∂y(j)l∂u(j)l∂u(j)l∂b(j)l=∂E∂y(j)lf′(u(j)l)
另有,下一层所有结点的输入都与前一层的每个结点输出有关,因此损失函数可以认为是下一层的每个神经元结点输入的函数。那么:
∂E∂y(j)l=∂E(u(1)l+1,u(2)l+1,...,u(k)l+1,...,u(K)l+1)∂y(j)l=∑k∈Ll+1∂E∂u(k)l+1∂u(k)l+1∂y(j)l=∑k∈Ll+1∂E∂y(k)l+1∂y(k)l+1∂u(k)l+1∂u(k)l+1∂y(j)l=∑k∈Ll+1∂E∂y(k)l+1∂y(k)l+1∂u(k)l+1w(kj)l+1
此处定义节点的灵敏度为误差对输入的变化率,即:
δ=∂E∂u
那么第
l
层第
j个节点的灵敏度为:
δ(j)l=∂E∂u(j)l=∂E∂y(j)l∂y(j)l∂u(j)l=∂E∂y(j)lf′(u(j)l)
结合灵敏度的定义,则有:
∂E∂y(j)l=∑k∈Ll+1∂E∂y(k)l+1∂y(k)l+1∂u(k)l+1w(kj)l+1=∑k∈Ll+1δkl+1w(kj)l+1
上式两边同时乘上
f′(u(j)l)
,则有
δ(j)l=∂E∂y(j)lf′(u(j)l)=f′(u(j)l)∑k∈Ll+1δkl+1w(kj)l+1
注意到上式中表达的是前后两层的灵敏度关系,而对于最后一层,也就是输出层来说,并不存在后续的一层,因此并不满足上式。但输出层的输出是直接和误差联系的,因此可以用损失函数的定义来直接求取偏导数。那么:
δ(j)l=∂E∂y(j)lf′(u(j)l)=⎧⎩⎨⎪⎪f′(u(j)l)∑k∈Ll+1δkl+1w(kj)l+1l层为隐层f′(u(j)l)(y(j)l−t(j))l层为输出层
至此,损失函数对各参数的梯度为:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∂E∂w(ji)l∂E∂b(j)l=∂E∂u(j)l∂u(j)l∂w(ji)l=δ(j)ly(i)l−1=∂E∂u(j)l∂u(j)l∂b(j)l=δ(j)l
上述的推到都是建立在单个节点的基础上,对于各层所有节点,采用矩阵的方式表示,则上述公式可以写成:
∂E∂Wl∂E∂blδl=δlyTl−1=δl={(WTl+1δl+1)∘f′(ul),l层为隐层(yl−t)∘f′(ul),l层为输出层
其中运算符
∘
表示矩阵或者向量中的对应元素相乘。
常见的几个激活函数的导数为:
f′(ul)f′(ul)f′(ul)=sigmoid′(ul)=sigmoid(ul)(1−sigmoid(ul))=yl(1−yl)=tanh′(ul)=1−tanh2(ul)=1−y2l=softmax′(ul)=softmax(ul)−softmax2(ul)=yl−y2l
根据上述公式,可以得到各层参数的更新公式为:
Wlbl:=Wl−η∂E∂Wl=Wl−ηδlyTl−1:=bl−η∂E∂b=bl−ηδl
References:



























 2169
2169

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








