目录
深度学习参数初始化系列:
一、介绍
Kaiming初始化论文地址:https://arxiv.org/abs/1502.01852
Xavier初始化在ReLU层表现不好,主要原因是relu层会将负数映射到0,影响整体方差。而且Xavier初始化方法适用的激活函数有限:要求关于0对称;线性。而ReLU激活函数并不满足这些条件,实验也可以验证Xavier初始化确实不适用于ReLU激活函数。所以何恺明在对此做了改进,提出Kaiming初始化,一开始主要应用于计算机视觉、卷积网络。
二、基础知识
1.假设随机变量X和随机变量Y相互独立,则有
![]() (1)
(1)
2.通过期望求方差的公式, 方差等于平方的期望减去期望的平方.
![]() (2)
(2)
3.独立变量乘积公式
![]() (3)
(3)
4.连续性随机变量X的概率密度函数为f(x),若积分绝对收敛,则期望公式如下:
![]() (4)
(4)
三、Kaiming初始化的假设条件
与Xavier初始化相似,Kaiming初始化同样适用Glorot条件,即我们的初始化策略应该使得各层的激活值和状态梯度的方差在传播过程中的方差保持一致;Kaiming初始化的参数仍然满足均值是0,且更新的过程中权重的均值一直是0。
与Xavier初始化不同的,Kaiming初始化不在要求每层输出均值都是0(因为Relu这样的激活函数做不到啊);当然也不再要求f′(0)=1。
Kaiming初始化中,前向传播和反向传播时各自使用自己的初始化策略,但是保证前向传播时每层的方差和反向传播时梯度的方差都是1。
四、Kaiming初始化的简单的公式推导
我们使用卷积来进行推导,并且激活函数使用ReLU。
1.前向传播
对于一层卷积,有:
![]() (5)
(5)
其中是激活函数前的输出,
是权重的个数,
是权重,
是输入。
根据(3)式,可将(4)式推导为:![]()
(6)
根据假设,但是
是上一层通过ReLU得到的,所以
,则:
![]()
![]() (7)
(7)
通过(2)式可得![]() ,则(7)式推导为:
,则(7)式推导为:
![]() (8)
(8)
根据期望公式(4), 通过第层的输出来求此期望, 我们有
, 其中
表示ReLU函数.
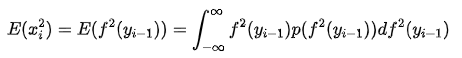 (9)
(9)
其中![]() 表示概率密度函数,因为
表示概率密度函数,因为的时候
,所以可以去掉小于0的区间, 并且大于0的时候
,可推出:
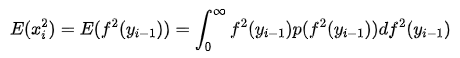 (10)
(10)
因为是假设在0周围对称分布且均值为0, 所以
也是在0附近分布是对称的, 并且均值为0(此处假设偏置为0),则
 (11)
(11)
所以的期望是:

 (12)
(12)
根据公式(2),因为的期望等于0,于是有:
![]()
则式(12)推导为:
 (13)
(13)
将(13)式带入(8)式:
![]() (14)
(14)
从第一层一直往前进行前向传播, 可以得到某层的方差为 :

这里的就是输入的样本, 我们会将其归一化处理, 所以
, 现在让每层输出方差等于1, 即:
![]()

于是正向传播时,Kaiming初始化的实现就是下面的均匀分布:

高斯分布:

2.反向传播
因为反向传播的时候
![]() (15)
(15)
其中表示损失函数并对其求导.
为参数
根据(3)式:
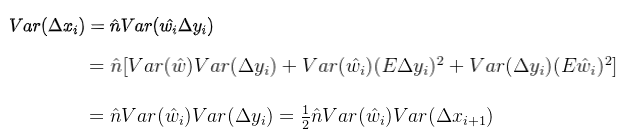
其中表示反向传播时输出通道数,最后得出

于是反向传播时,Kaiming初始化的实现就是下面的均匀分布:

高斯分布:
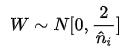
五、Pytorch实现
import torch
class DemoNet(torch.nn.Module):
def __init__(self):
super(DemoNet, self).__init__()
self.conv1 = torch.nn.Conv2d(1, 1, 3)
print('random init:', self.conv1.weight)
'''
kaiming 初始化方法中服从均匀分布 U~(-bound, bound), bound = sqrt(6/(1+a^2)*fan_in)
a 为激活函数的负半轴的斜率,relu 是 0
mode- 可选为 fan_in 或 fan_out, fan_in 使正向传播时,方差一致; fan_out 使反向传播时,方差一致
nonlinearity- 可选 relu 和 leaky_relu ,默认值为 。 leaky_relu
'''
torch.nn.init.kaiming_uniform_(self.conv1.weight, a=0, mode='fan_out')
print('xavier_uniform_:', self.conv1.weight)
'''
kaiming 初始化方法中服从正态分布,此为 0 均值的正态分布,N~ (0,std),其中 std = sqrt(2/(1+a^2)*fan_in)
a 为激活函数的负半轴的斜率,relu 是 0
mode- 可选为 fan_in 或 fan_out, fan_in 使正向传播时,方差一致;fan_out 使反向传播时,方差一致
nonlinearity- 可选 relu 和 leaky_relu ,默认值为 。 leaky_relu
'''
torch.nn.init.kaiming_normal_(self.conv1.weight, a=0, mode='fan_out')
print('kaiming_normal_:', self.conv1.weight)
if __name__ == '__main__':
demoNet = DemoNet()还在为找工作烦恼吗,用这个宝藏小程序,拿Offer快人一步!Offer入口》》》


























 1158
1158

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










