Coder
Time Limit: 20000/10000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 2096 Accepted Submission(s): 858
Problem Description
In mathematics and computer science, an algorithm describes a set of procedures or instructions that define a procedure. The term has become increasing popular since the advent of cheap and reliable computers. Many companies now employ a single coder to write an algorithm that will replace many other employees. An added benefit to the employer is that the coder will also become redundant once their work is done.
1
You are now the signle coder, and have been assigned a new task writing code, since your boss would like to replace many other employees (and you when you become redundant once your task is complete).
Your code should be able to complete a task to replace these employees who do nothing all day but eating: make the digest sum.
By saying “digest sum” we study some properties of data. For the sake of simplicity, our data is a set of integers. Your code should give response to following operations:
1. add x – add the element x to the set;
2. del x – remove the element x from the set;
3. sum – find the digest sum of the set. The digest sum should be understood by
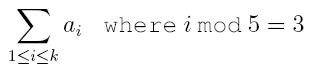
where the set S is written as {a 1, a 2, ... , a k} satisfying a 1 < a 2 < a 3 < ... < a k
Can you complete this task (and be then fired)?
------------------------------------------------------------------------------
1 See http://uncyclopedia.wikia.com/wiki/Algorithm
You are now the signle coder, and have been assigned a new task writing code, since your boss would like to replace many other employees (and you when you become redundant once your task is complete).
Your code should be able to complete a task to replace these employees who do nothing all day but eating: make the digest sum.
By saying “digest sum” we study some properties of data. For the sake of simplicity, our data is a set of integers. Your code should give response to following operations:
1. add x – add the element x to the set;
2. del x – remove the element x from the set;
3. sum – find the digest sum of the set. The digest sum should be understood by
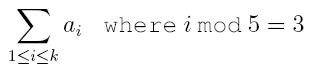
where the set S is written as {a 1, a 2, ... , a k} satisfying a 1 < a 2 < a 3 < ... < a k
Can you complete this task (and be then fired)?
------------------------------------------------------------------------------
1 See http://uncyclopedia.wikia.com/wiki/Algorithm
Input
There’re several test cases.
In each test case, the first line contains one integer N ( 1 <= N <= 10 5 ), the number of operations to process.
Then following is n lines, each one containing one of three operations: “add x” or “del x” or “sum”.
You may assume that 1 <= x <= 10 9.
Please see the sample for detailed format.
For any “add x” it is guaranteed that x is not currently in the set just before this operation.
For any “del x” it is guaranteed that x must currently be in the set just before this operation.
Please process until EOF (End Of File).
In each test case, the first line contains one integer N ( 1 <= N <= 10 5 ), the number of operations to process.
Then following is n lines, each one containing one of three operations: “add x” or “del x” or “sum”.
You may assume that 1 <= x <= 10 9.
Please see the sample for detailed format.
For any “add x” it is guaranteed that x is not currently in the set just before this operation.
For any “del x” it is guaranteed that x must currently be in the set just before this operation.
Please process until EOF (End Of File).
Output
For each operation “sum” please print one line containing exactly one integer denoting the digest sum of the current set. Print 0 if the set is empty.
Sample Input
9 add 1 add 2 add 3 add 4 add 5 sum add 6 del 3 sum 6 add 1 add 3 add 5 add 7 add 9 sum
Sample Output
3 4 5HintC++ maybe run faster than G++ in this problem.本题即将区间内的元素按升序排列,然后求下标对5取摸余3的数的和,由于需要升序排列,当来一个数的时候就把他插入到适当位置,这就要求实现读入所有数据,然后离散化处理建立区间,当加操作时就把元素插到适当区间,当修改元素时就把适当位置置零,关键是求和时候的根据下标对5取摸余3,由于是递归,先左子树后右子树,所以左边的不变,右边的需(i-tree[id*2].num%5+5)%5,具体数学道理有待想想,本题关键是先离散化处,防止MLT#include<iostream> #include<cstdio> #include<algorithm> using namespace std; const int MAX=100000+10; char cmd[MAX][5]; __int64 a[MAX]; __int64 ta[MAX]; int da[MAX]; struct node { int left,right,num; __int64 sum[5]; }tree[MAX*3]; void build( int id, int left, int right ) { tree[id].left = left; tree[id].right = right; tree[id].num=0; memset(tree[id].sum,0,sizeof(tree[id].sum)); if( left == right ) { return ; } else { int mid = ( left + right )/2; build( id * 2, left, mid ); build( id * 2 + 1, mid + 1, right ); } } void pushup(int id) { int i; for(i=0;i<5;i++) tree[id].sum[i]=tree[id*2].sum[i]+tree[id*2+1].sum[(i-tree[id*2].num%5+5)%5];//tree[id*2+1].sum[(1+i+tree[id*2].num%5)%5]; } void updata(int id,int pos,bool flag) { if(flag)tree[id].num++; else tree[id].num--; if(tree[id].left==tree[id].right ) { if(flag) tree[id].sum[1]=ta[pos]; else tree[id].sum[1]=0; return ; } int mid = (tree[id].left+tree[id].right) /2; if(pos<=mid) updata( id * 2,pos,flag); else updata( id * 2 + 1,pos,flag); pushup(id); } int main() { int n,i,num,cnt; while(~scanf("%d",&n)) { num=0; for(i=0;i<n;i++) { scanf("%s",cmd[i]); if(cmd[i][0]!='s') { scanf("%d",&a[i]); ta[num]=a[i]; num++; } } sort(ta,ta+num); int cnt=unique(ta,ta+num)-ta; build(1,1,cnt); // cout<<cnt<<endl; for(i=0;i<n;i++) { int ind=lower_bound(ta,ta+cnt,a[i])-ta; // printf(" %I64d pos=%d\n",a[i],ind); if(cmd[i][0]=='a') { updata(1,ind,true); } else if(cmd[i][0]=='d') { updata(1,ind,false); } else { printf("%I64d\n",tree[1].sum[3]); } } } return 0; }






















 447
447

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








