矩阵 向量 线性变换 基变换

线性变换：

1.features

函数的一种比较 “花哨” 的说法，只不过它接收一个向量，并输出一个向量

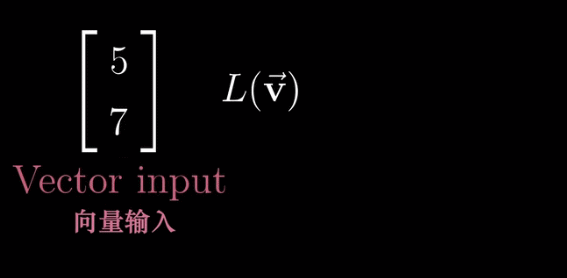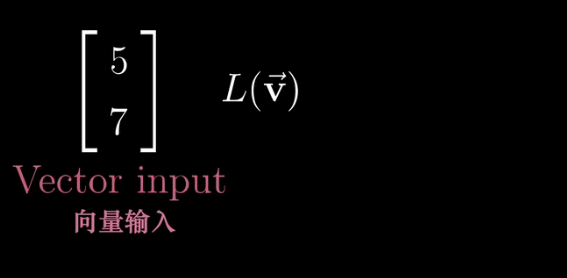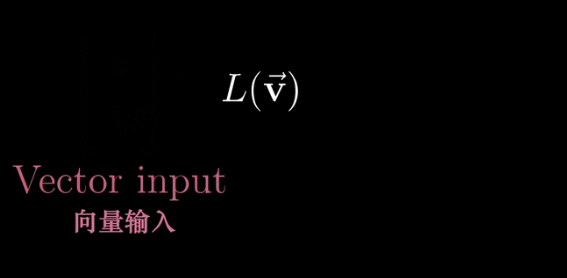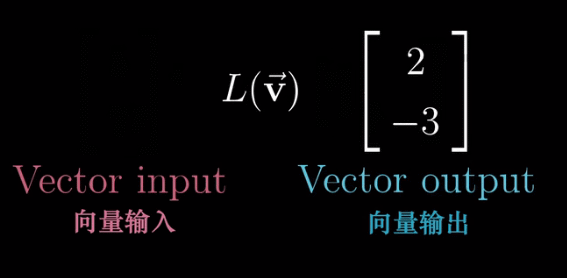
但是满足线性变换还需要满足以下条件

1.  ：

2. 

=============================================================

参考百度百科：https://baike.baidu.com/item/%E7%BA%BF%E6%80%A7%E5%8F%98%E6%8D%A2/5904192?fr=aladdin

线性空间V上的一个变换A称为线性变换，对于V中任意的元素α，β和数域P中任意k，都有

A(α+β)=A（α）+A（β）

A (kα)=kA(α)

=============================================================

若我们记录空间中所有的向量，都只记录终点，空间中所有向量都经过L进行线性变换，我们很难用图像描述所有的向量，只能抽一些终点在特定直线上的向量作为代表，例如我们可以抽取终点 在 经过整数刻度的直线 上的向量作为代表，如下图：

这样我们可以通过网格的变换来直观地呈现空间中向量的变换，甚至整个空间的形状的变换如下图：

所以线性变换在图像上的直观呈现就是：

1.变换前后空间中的网格线 仍然是等间距的、平行的直线

2.零向量经过线性变换后仍然是零向量，即线性变换前后空间的原点不会改变

Grid lines remain parallel and evenly spaced

2.how to describe liner transformation numerically?

我们只需要记录变换后基向量的坐标即可

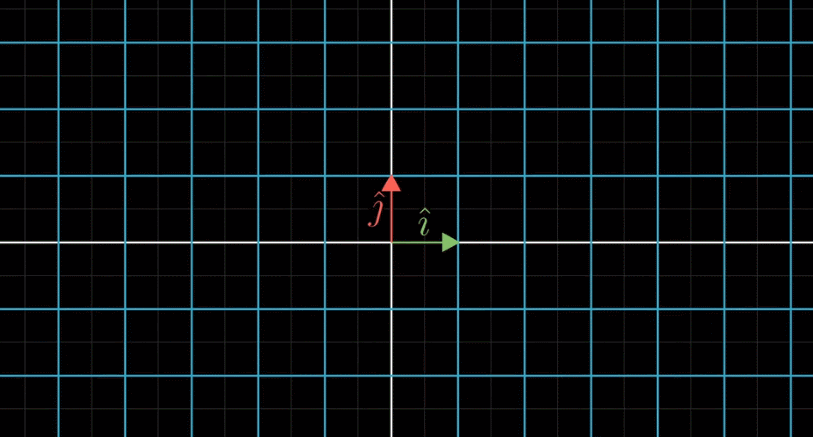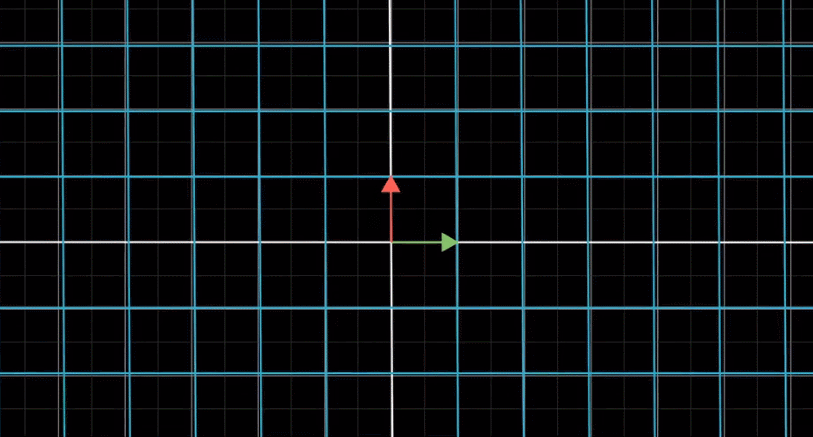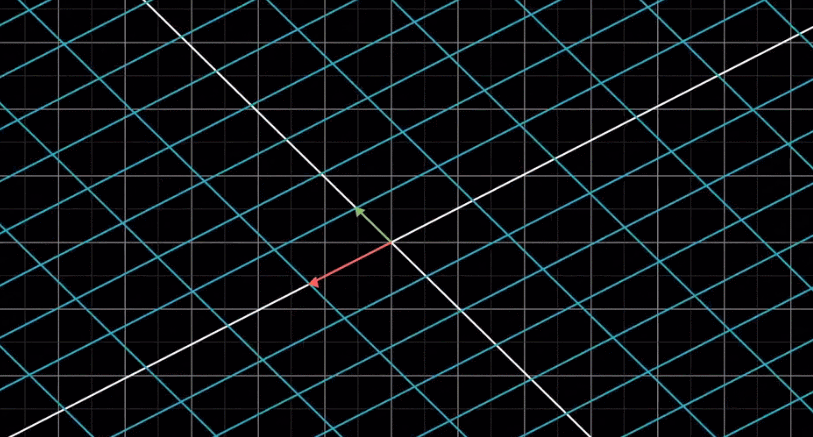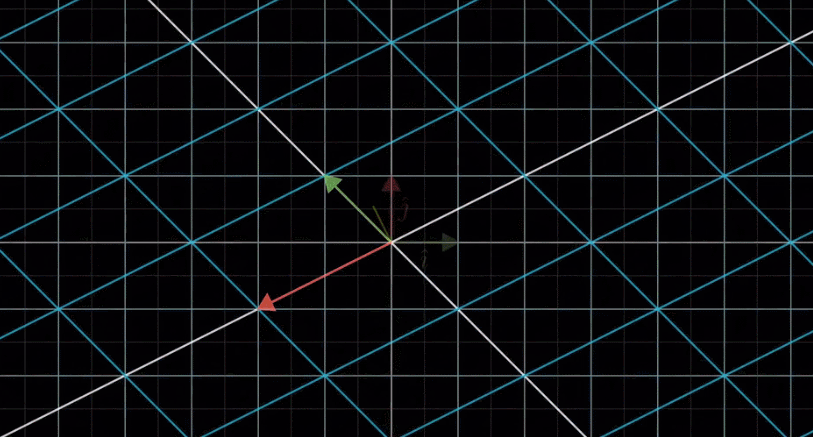
假设有一个向量

根据线性变换的特性 平行且等距，变换后的 v 和变换后的 i 和 j 仍然满足以上关系，另外也可以根据上述公式特性进行以下推导：

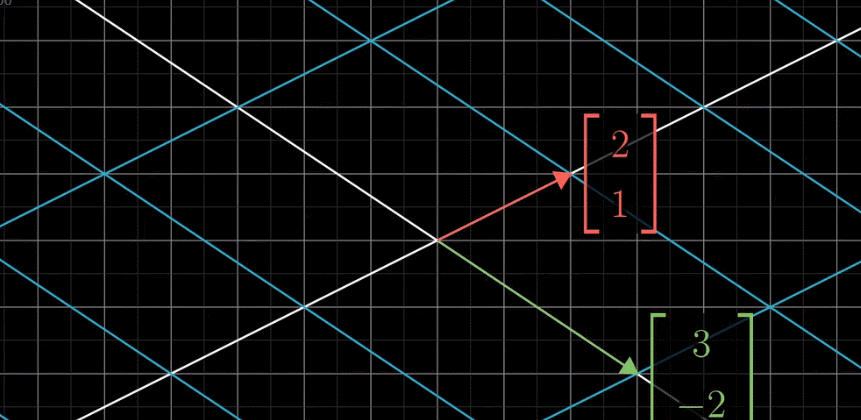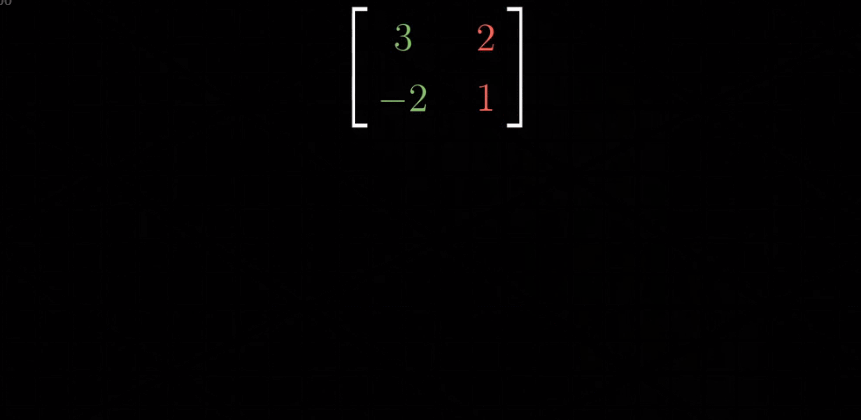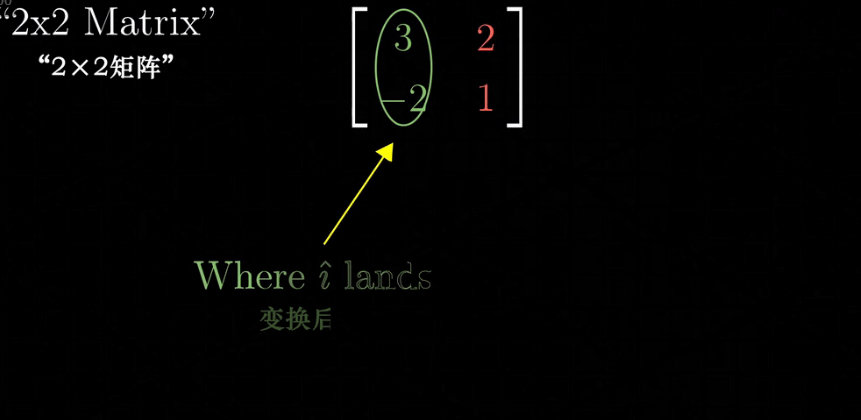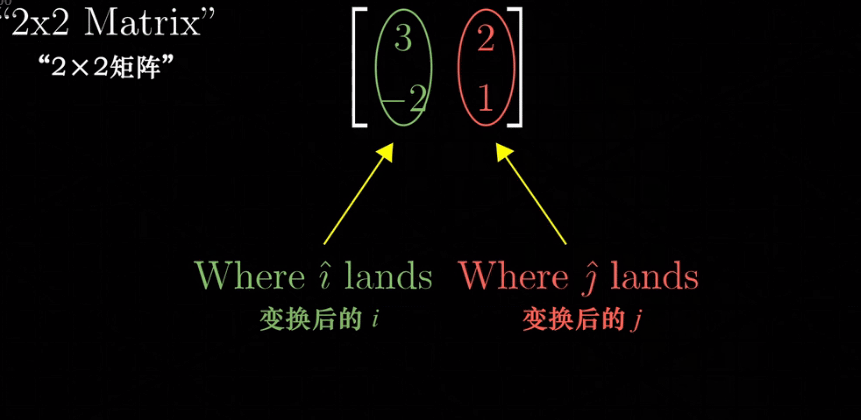
所以我们只需要记录变换后的基向量即可计算出变换后所有向量的坐标，如下图：

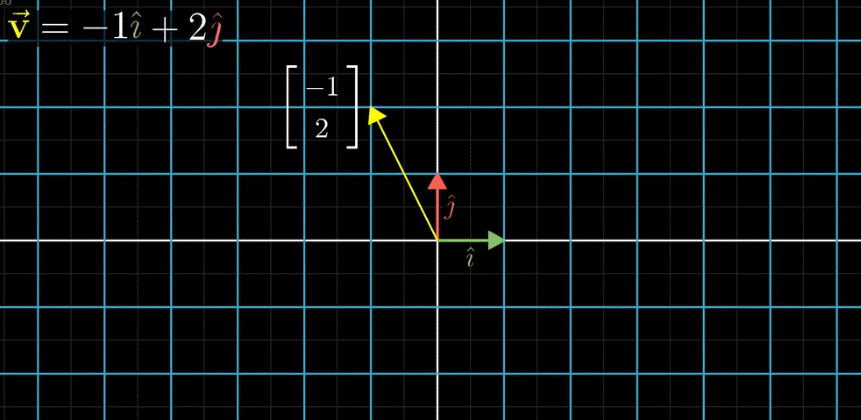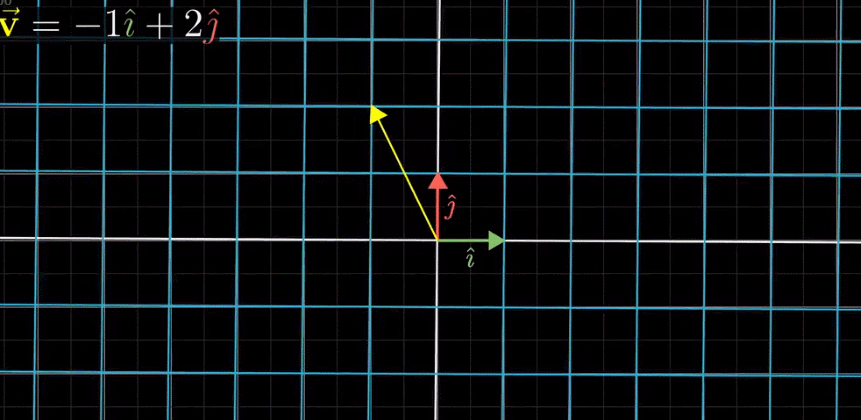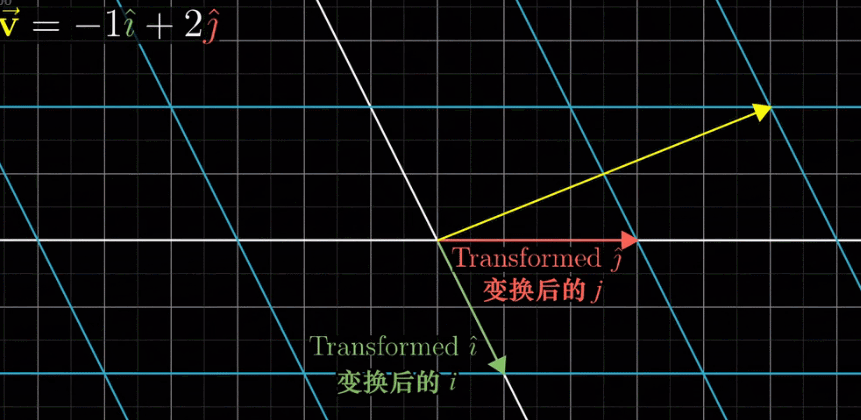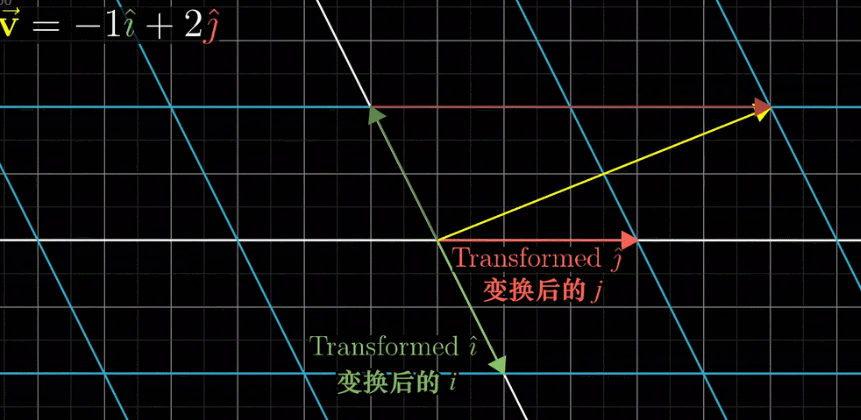
由上图可知，向量 v 是向量 i 和向量  j 的线性组合，那么变换后的向量 v 仍然是变换后的向量 i 和变换后的向量 j 同样的线性组合。

以上一切都是在说，一个线性变换，这里以二维变换为例，一个线性二维变换只需要四个数字完全确定，其中2个数字描述变换后的基向量 i 在原始坐标系中的坐标，另外2个数字描述变换后基向量 j 在原始坐标系中的坐标。这样我们就将4个数字封装到一个2x2的格子中，称为2x2的矩阵，所以这里给出了描述矩阵的另一种方式，矩阵（可以延伸到非方针）描述的一种线性变换，矩阵的每一列 描述的是 经历这种线性变换后 的基向量在原始坐标系中的新的坐标，如下图：

矩阵

每个矩阵都对应一种线性变换，那么我们如何得到  将这种线性变换作用到向量后的结果，我们只需要将向量的坐标分别乘以矩阵的每一列（变换后的基向量坐标），然后在相加即可，我们甚至可以将其定义为矩阵的乘法：

重复上述说法，我们完全可以将矩阵的每一列看做变换后的基向量，如下图：

多个矩阵相乘可以看做多个线性变换的复合变换：

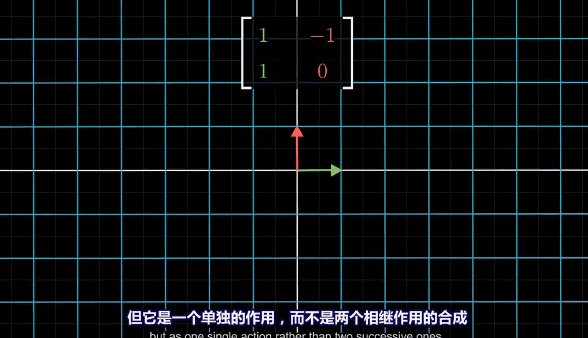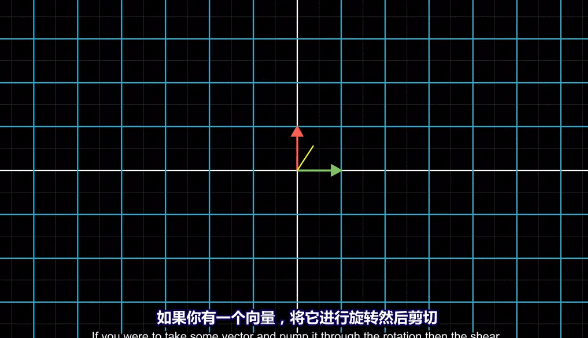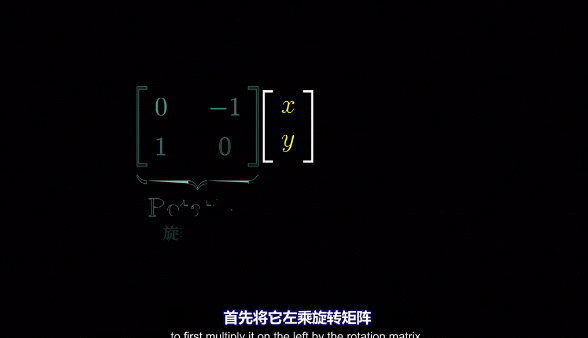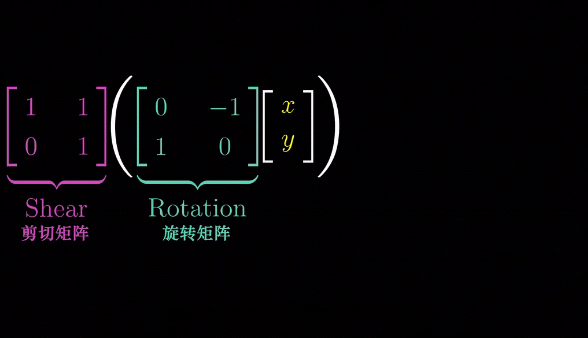
基变换

我们使用坐标表示向量，实际上包含两个隐含假设，

即基向量如上图所示，但是如果选取不同的基向量会怎么样呢，比如你的朋友Jennifer使用一下不同的基向量 b1、b2：

Jennifer的基向量在我们的坐标系中的坐标为  

在她自己坐标系中的坐标为   

 

1.How do you translate between coordinate systems?

如何在不同的坐标系中进行坐标变换呢？

假如Jennifer用(-1, 2)描述一个向量，那么我们应该如何用我们的坐标系来描述这个向量呢？

我们可以用-1乘以b1向量在我们坐标系的坐标，2乘以b2向量在我们坐标系的坐标，然后相加：

这样我们就可以由一个向量在Jennifer坐标系下的坐标，就能推算出它在我们坐标系下的坐标，即将Jennifer的语言翻译成我们的语言。

 

如果相反方向会怎么样的，例如我们用(3, 2)描述一个向量，那么在Jennifer的坐标系中怎么描述这个向量？

这个矩阵可以将我们坐标系中基向量变换成Jennifer坐标系中的基向量，Jennifer坐标系的基向量在我们坐标系中的坐标就是(2,1)、(-1, 1)，根据矩阵的定义，矩阵的每一列代表线性变换后的坐标系的基向量在原始坐标系的坐标而来。

这个矩阵可以将Jennifer坐标系中的基向量变换为我们坐标系中的基向量，同理根据矩阵的定义，矩阵的每一列代表，线性变换后的坐标系的基向量（我们坐标系的基向量）在原始坐标系（Jennifer）中的坐标，所以我们坐标系的基向量i、j在Jennifer坐标系中的坐标分别是(1/3, -1/3)、(1/3, 2/3)

回到原来的问题：我们用(3, 2)描述一个向量，那么在Jennifer的坐标系中怎么描述这个向量？

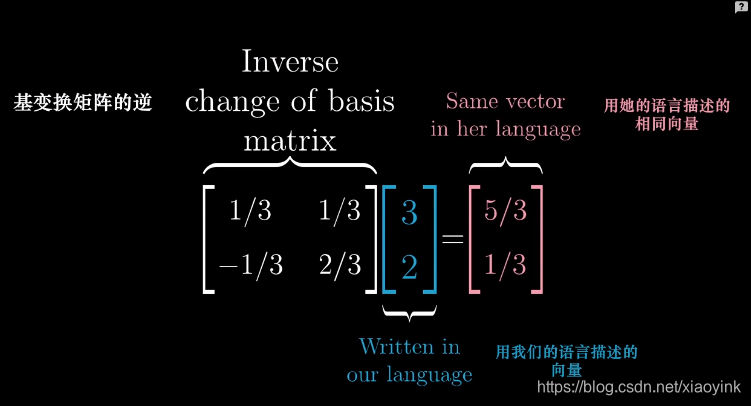
如上图所示，在Jennifer眼中此向量的坐标为(5/3, 1/3)

 

以上所有内容均参考3blue1brown官方发布的视频，它们在中国的官方账号是在bilibili，线性代数这一节的网址如下：  https://space.bilibili.com/88461692/channel/detail?cid=9450

Youtube网站的官方账号如下：

https://www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw