Prim — 求最小生成树（算法详解，图论，附例题、代码）

目录

概述

原理介绍

例题

题目

样例

Code

Dijkstra和Prim

总结

---

概述

Prim算法用于解决最小生成树问题。

生成树是可以视作一个无向、无环、带权的图（也可以说是树），任意两个节点有且仅有一条简单路径连接。最小生成树问题是，在一个复杂的、带环的图中找到一棵树，使这棵树包含所有的节点，并且权重之和最小。

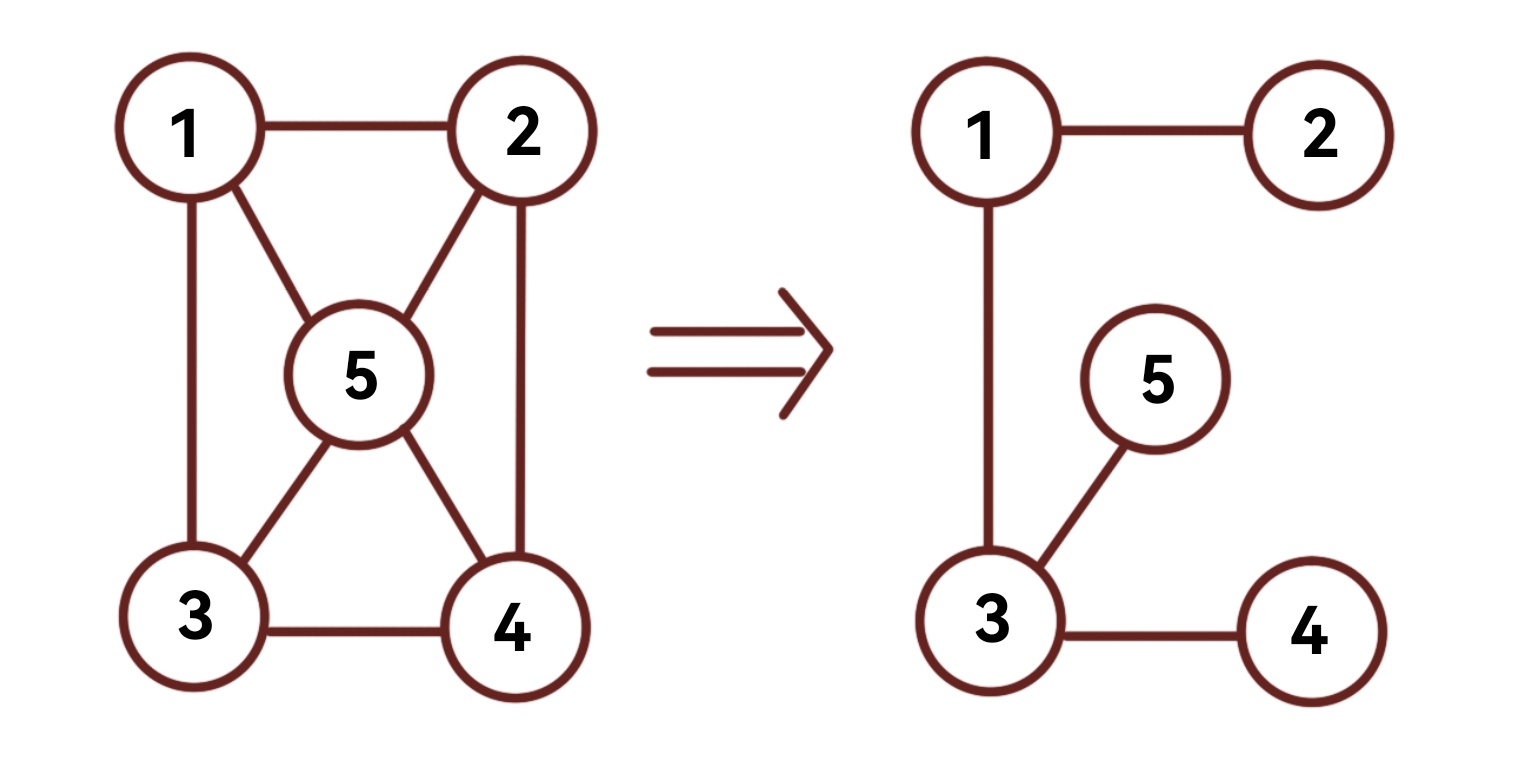
原理介绍

Prim算法的主要思想是贪心。我们将节点分为两个集合：已放入生成树（u）和未放入生成树中（v）中。每次将从集合 v 选中距离集合 u 最近的点，并不断更新。为实现这个目的，我们维护一个dist[]数组和一个visited[]数组，并规定：

1、图的邻接矩阵中，若a、b间无边，将其距离视为∞(为显示直观并且防止溢出，可设为MAX=INT_MAX/2)

2、dist[i]数组表示目前更新到的 i 节点距离集合 v 的最短距离(节点i来自集合 u )。

3、visited[i]为真表示该节点源于集合u；visited[i]为假表示该节点源于集合v。

我们进行以下步骤：

1、初始化邻接矩阵、dist数组和visited数组

2、扫描dist数组，找出集合v中距离集合u最近的节点i（若visited[i]=false，该节点属于集合v）

3、i距离集合u的最短距离已被找到，将visited[i]设为1

4、找出集合u中与i相邻的节点并更新他们与集合u的最短距离。

5、重复2~4

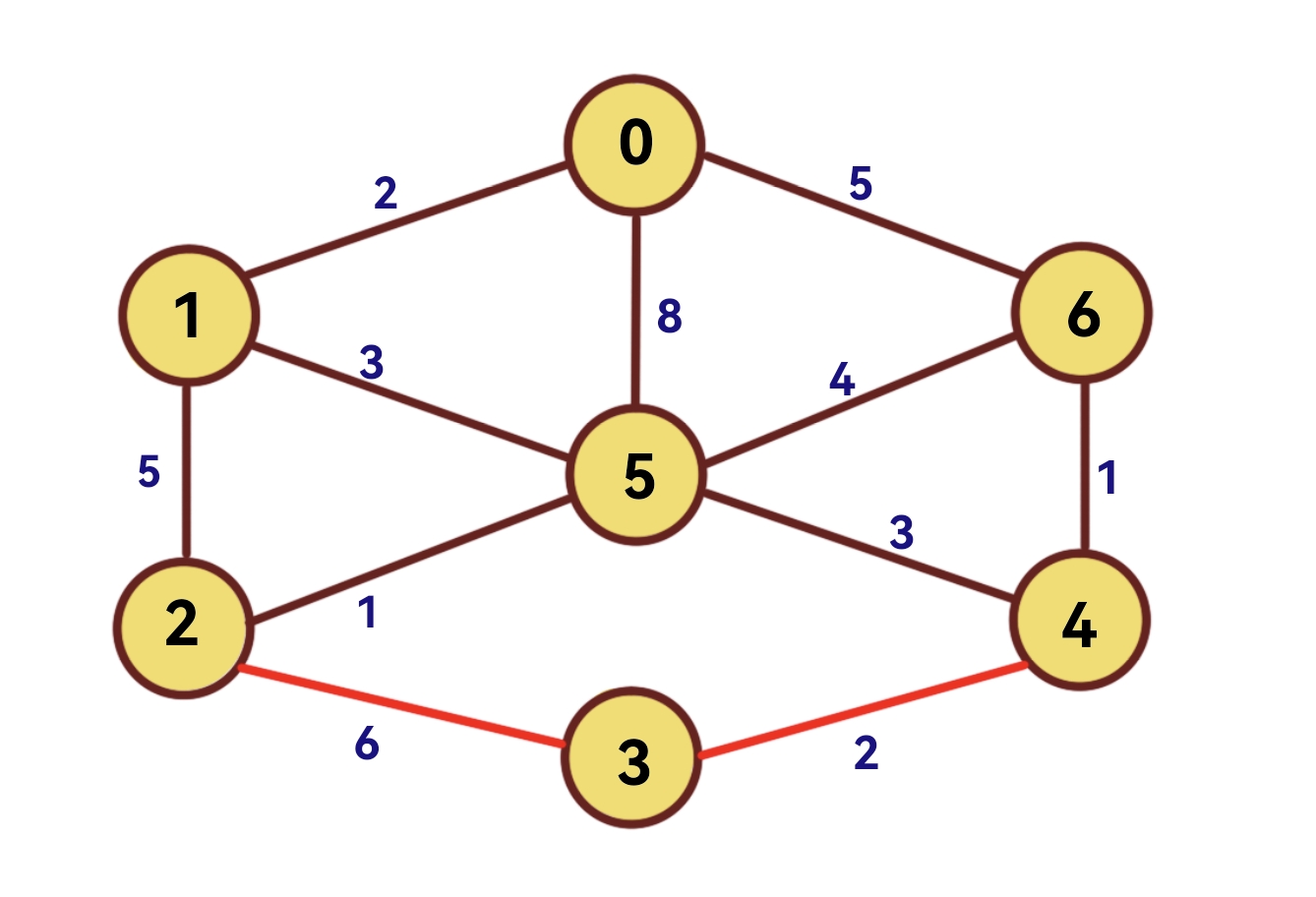
请看下面这个例子：

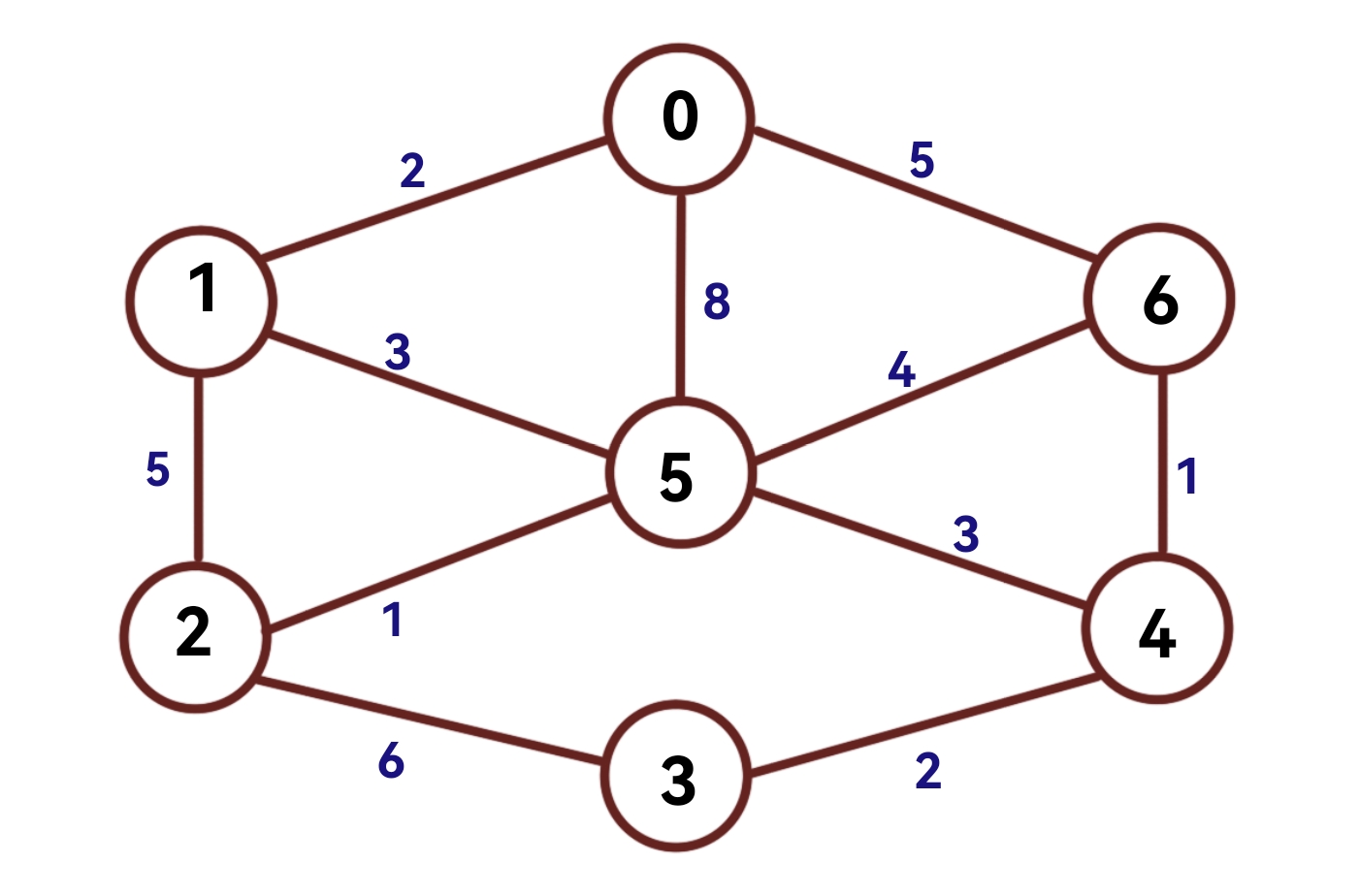
（1）初始化

将任意点放入集合u中，这里放入节点0。

初始化阶段把节点dist[0]初始化为0，其余为MAX。(节点0到节点0的最短距离为0，其他点还未扫描到，可暂时用MAX初始化。

节点	0	1	2	3	4	5	6
dist	0	MAX	MAX	MAX	MAX	MAX	MAX
visited	0	0	0	0	0	0	0

（2）第一次扫描

扫描dist数组，距离集合u最近的节点为0，因此0到集合u的最短距离为0。

将visited[ 0 ]设为1。

将其余点设为： dist[i] = min (G[ A ][i] ,dist[i])

(节点0到集合u的最短距离已经求出，更新与节点0相邻的节点i到集合u的距离，即G[A][i]，该点有可能比原本的dist[i]大，取最小)

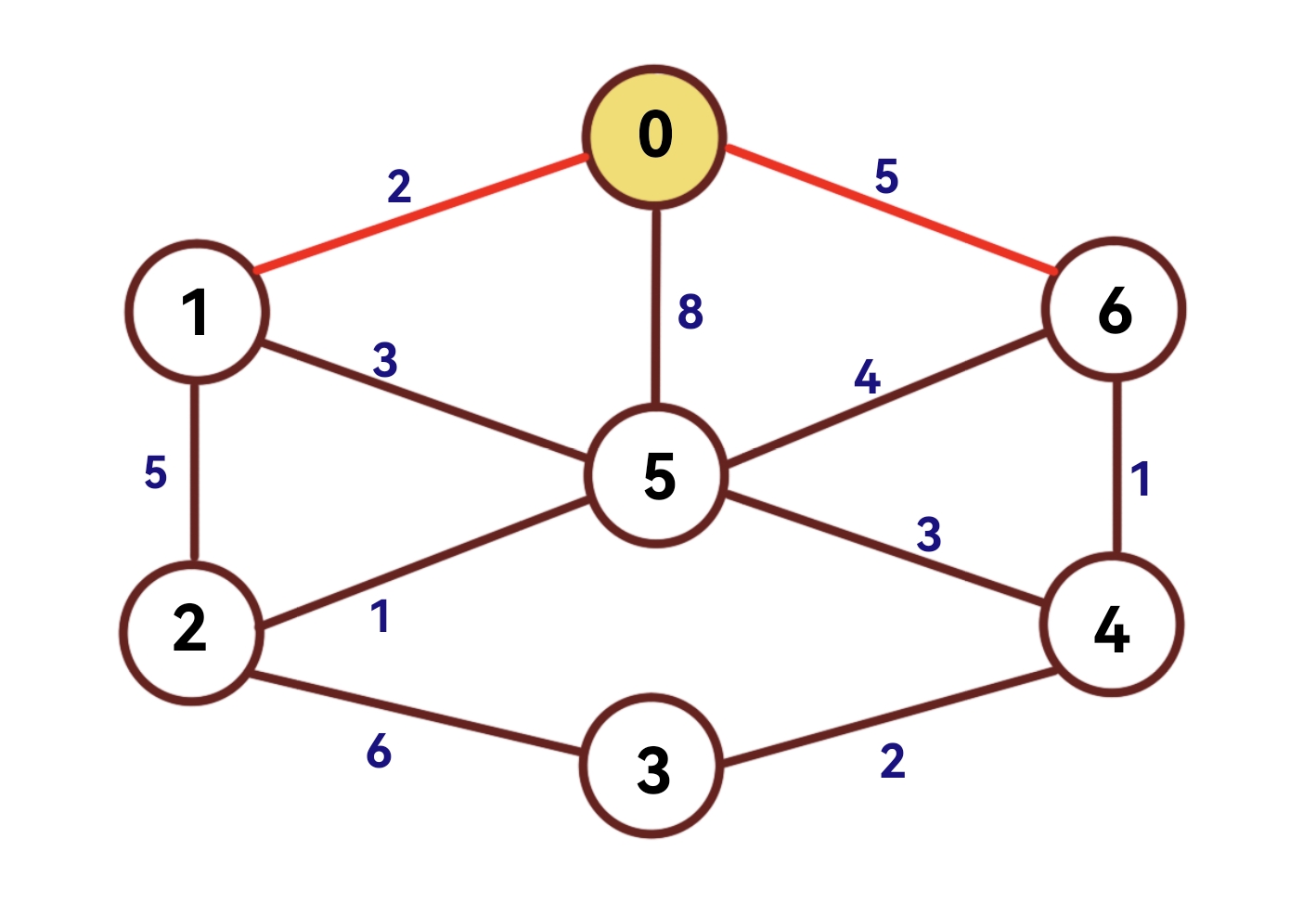
节点1、6与节点0直接相接，他们的dist[]被更新。

节点	0	1	2	3	4	5	6
dist	0	2	MAX	MAX	MAX	MAX	5
visited	1	0	0	0	0	0	0

（3）第二次扫描

扫描dist数组，距离集合u最近的节点为1，因此1到集合u的最短距离为dist[1]=2。

将visited[ 1 ]设为1。

将其余点设为： dist[i] = min (G[ A ][i] ,dist[i])

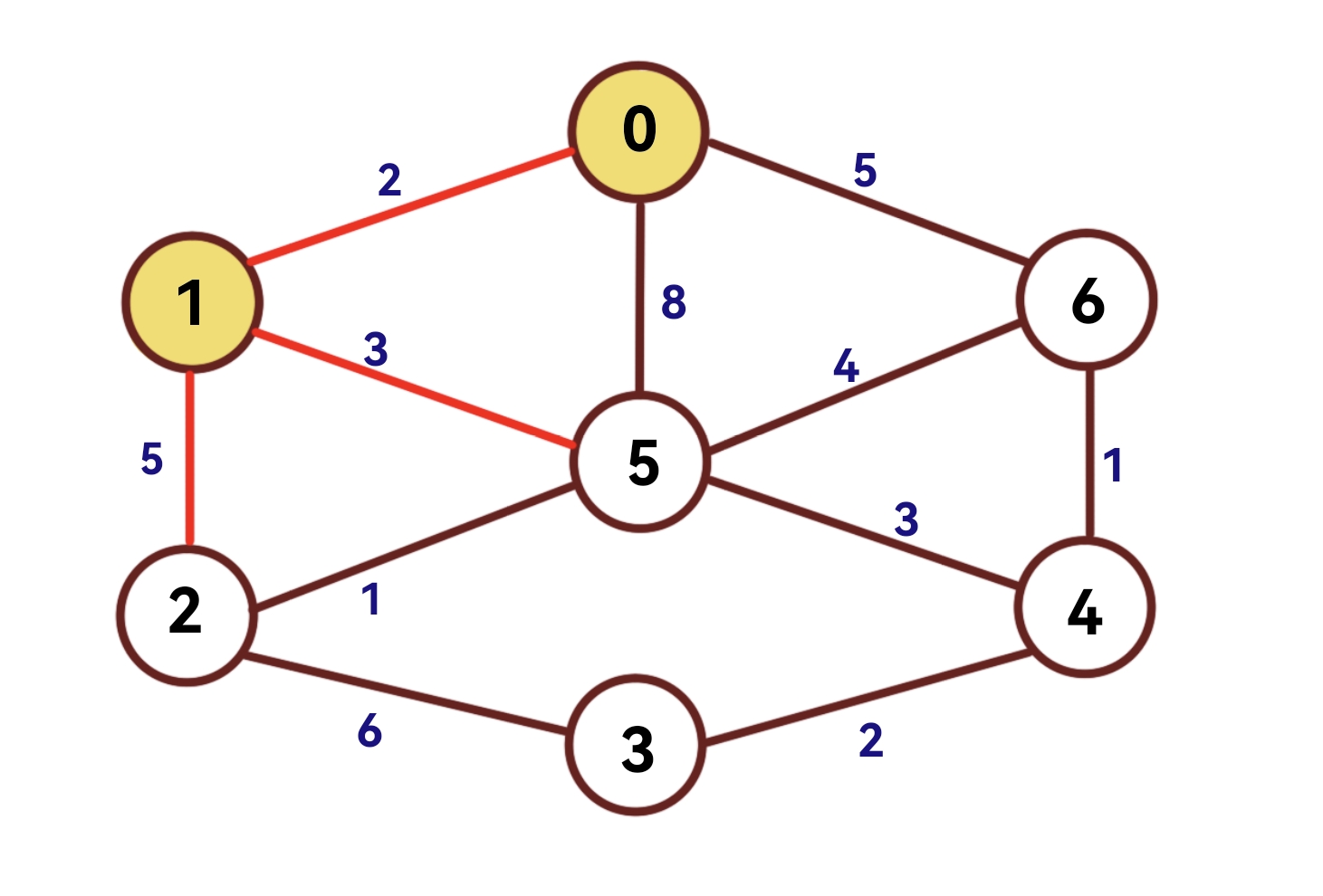
节点0、2、5与节点1直接相接，节点0已属于集合u，无需更新，其他节点的dist[]被更新。

节点	0	1	2	3	4	5	6
dist	0	2	5	MAX	MAX	3	5
visited	1	1	0	0	0	0	0

（4）第三次扫描

扫描dist数组，距离集合u最近的节点为5，因此5到集合u的最短距离为dist[5]=3。

将visited[ 5 ]设为1。

将其余点设为： dist[i] = min (G[ A ][i] ,dist[i])

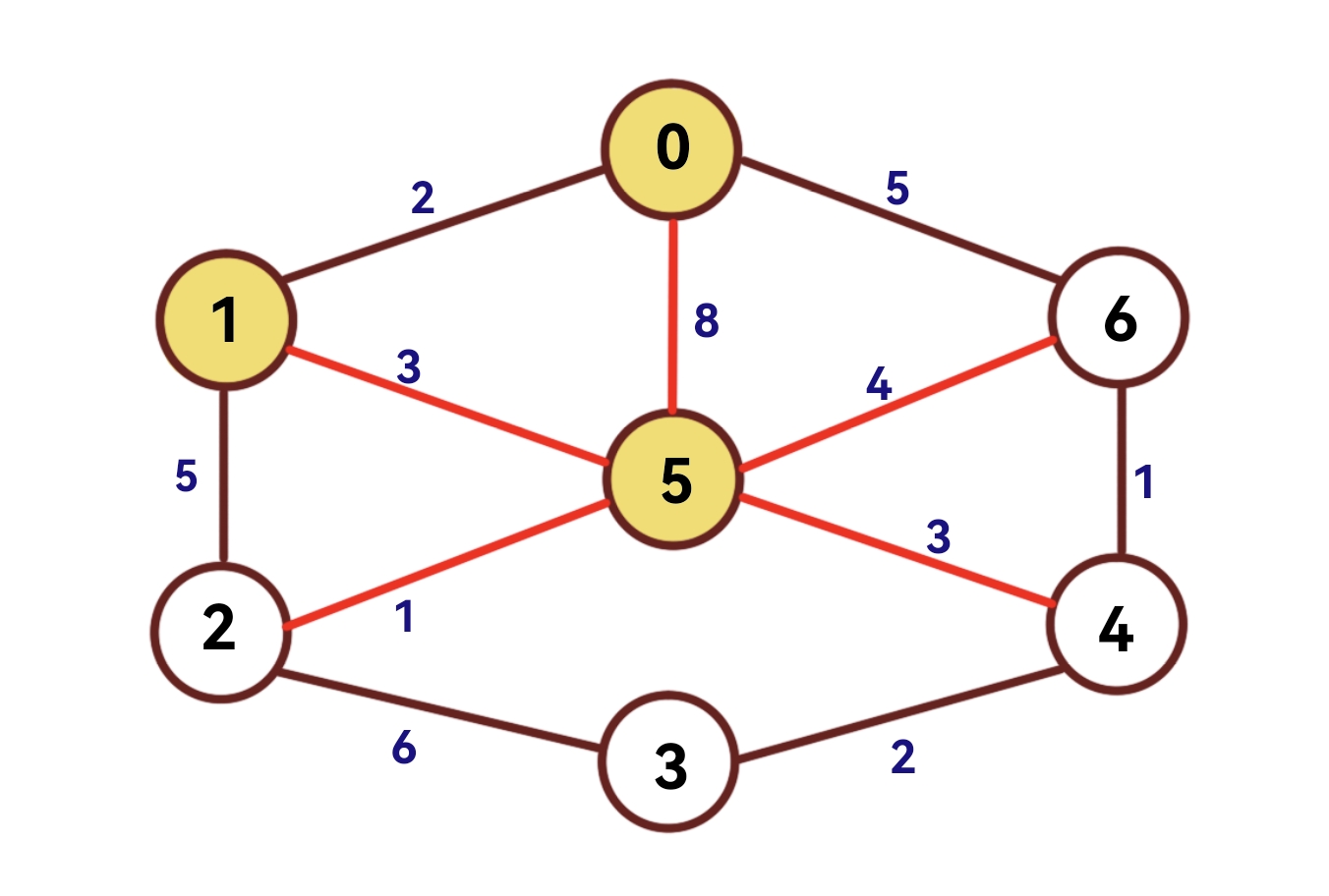
节点	0	1	2	3	4	5	6
dist	0	2	1	MAX	3	3	4
visited	1	1	0	0	0	1	0

（5）第四次扫描

扫描dist数组，距离集合u最近的节点为2，因此2到集合u的最短距离为dist[2]=1。

将visited[ 2 ]设为1。

将其余点设为： dist[i] = min (G[ A ][i] ,dist[i])

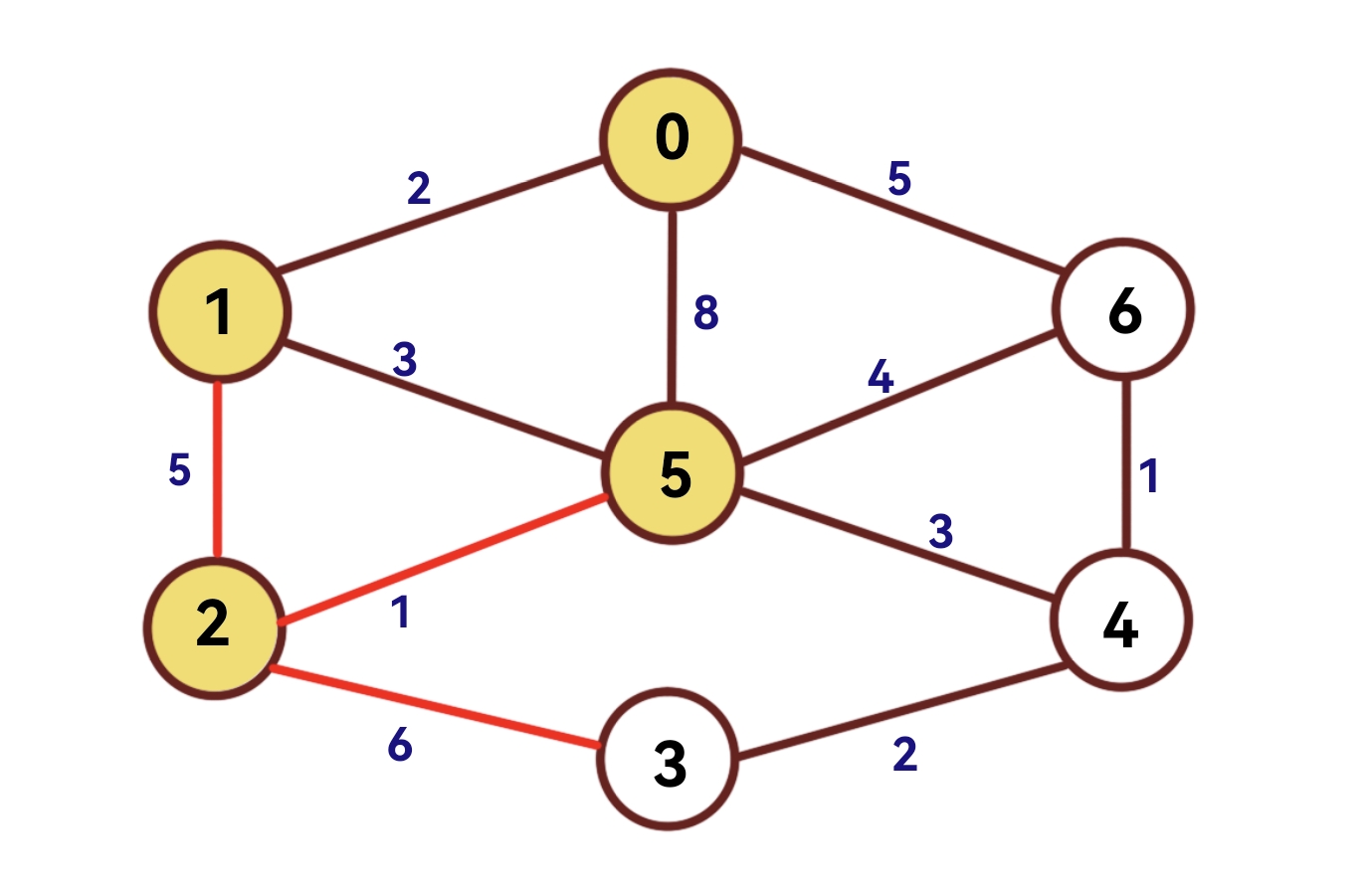
节点	0	1	2	3	4	5	6
dist	0	2	1	6	3	3	4
visited	1	1	1	0	0	1	0

（6）第五次扫描

扫描dist数组，距离集合u最近的节点为4，因此4到集合u的最短距离为dist[4]=3。

将visited[ 4 ]设为1。

将其余点设为： dist[i] = min (G[ A ][i] ,dist[i])

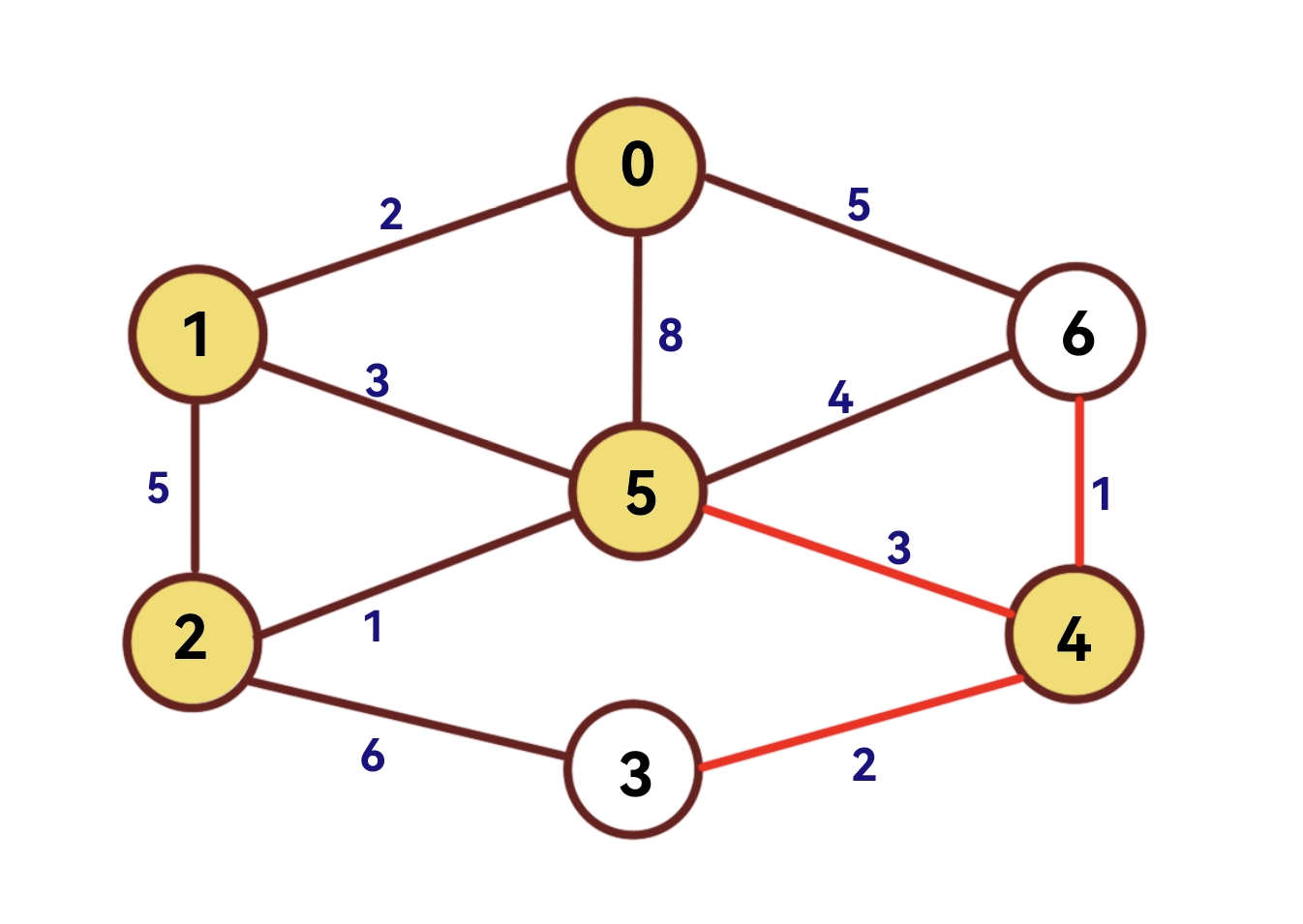
节点	0	1	2	3	4	5	6
dist	0	2	1	2	3	3	1
visited	1	1	1	0	1	1	0

（7）第六次扫描

扫描dist数组，距离集合u最近的节点为6，因此6到集合u的最短距离为dist[6]=1。

将visited[ 4 ]设为1。

将其余点设为： dist[i] = min (G[ A ][i] ,dist[i])

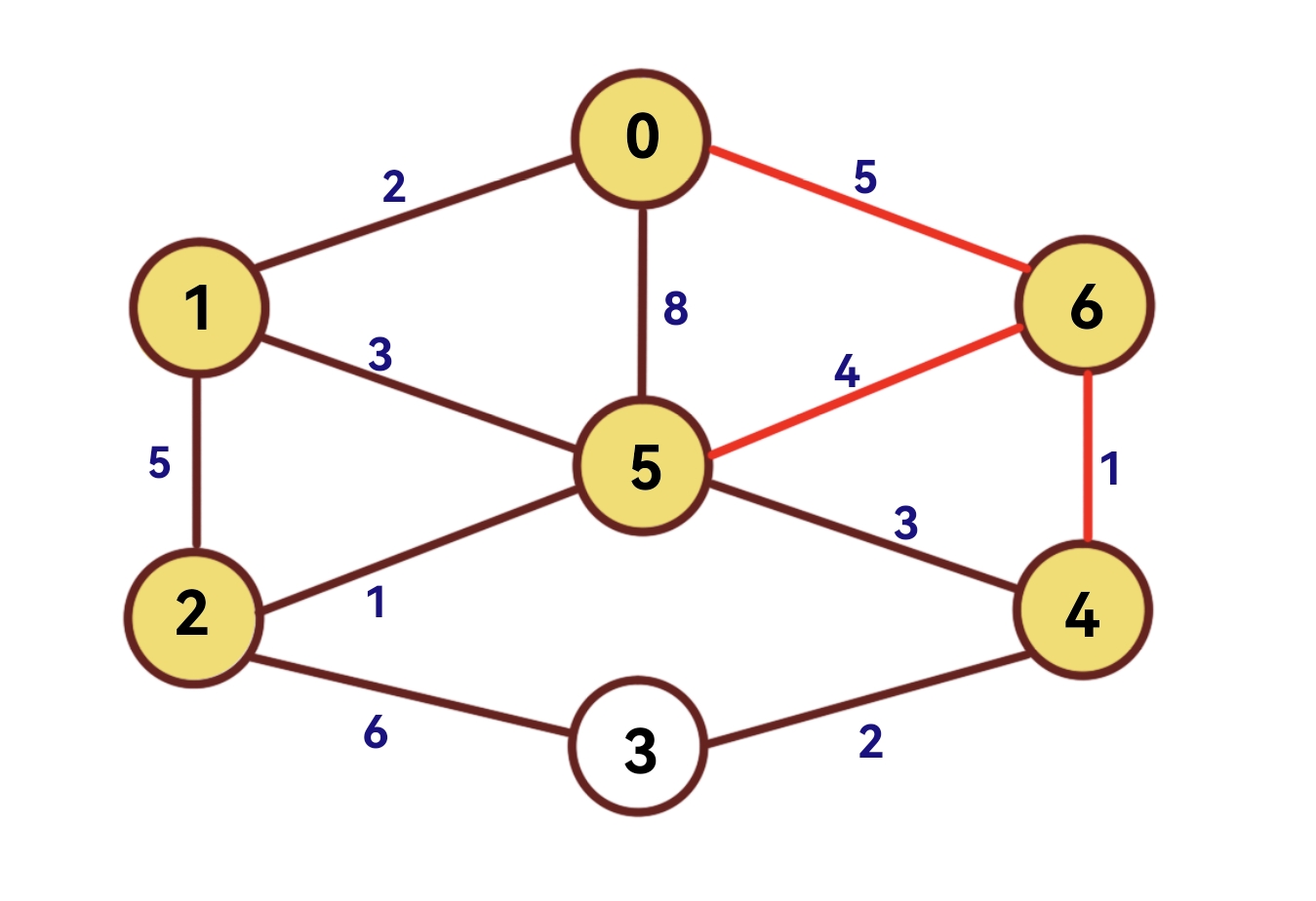
节点	0	1	2	3	4	5	6
dist	0	2	1	2	3	3	1
visited	1	1	1	0	1	1	1

（8）第七次扫描

扫描dist数组，距离集合u最近的节点为3，因此3到集合u的最短距离为dist[3]=2。

将visited[ 3 ]设为1。

将其余点设为： dist[i] = min (G[ A ][i] ,dist[i])

节点	0	1	2	3	4	5	6
dist	0	2	1	2	3	3	1
visited	1	1	1	1	1	1	1

（9）第八次扫描

扫描dist数组，所有节点均已放入生成树，最小生成树建立完毕。返回。

例题

题目来源：1584. 连接所有点的最小费用 - 力扣（LeetCode）

题目

给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

样例

示例 1：

输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]

输出：20

解释：

我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。

注意到任意两个点之间只有唯一一条路径互相到达。

示例 2：

输入：points = [[3,12],[-2,5],[-4,1]]

输出：18

示例 3：

输入：points = [[0,0],[1,1],[1,0],[-1,1]]

输出：4

示例 4：

输入：points = [[-1000000,-1000000],[1000000,1000000]]

输出：4000000

示例 5：

输入：points = [[0,0]]

输出：0

Code

int minCostConnectPoints(vector<vector<int>>& points) {
    const int MAX=INT_MAX/2;
    int n=points.size();

    ///建立邻接矩阵
    vector<vector<int>>g(n,vector<int>(n,MAX));  
    for(int i=0;i<n;i++){
        for(int j=i+1;j<n;j++){
            int d=abs(points[i][0]-points[j][0])+abs(points[i][1]-points[j][1]);
            g[i][j]=g[j][i]=d;
        }
    }

    vector<int>dist(n,MAX);
    vector<bool>visited(n,false);
    dist[0]=0;
    int res=0;

    while(1){
        int x=-1;
        for(int i=0;i<n;i++){
            if(!visited[i]&&(x==-1||dist[i]<dist[x])){
                x=i;
            }
        }

        if(x==-1)break;    ///所有节点被放入集合u，最小生成树已建立
               
        visited[x]=true;
        for(int i=0;i<n;i++){	///更新与x相邻的点的距离
            if(!visited[i])
                dist[i]=min(dist[i],g[x][i]);
        }
        res+=dist[x];	///更新总权值
    }
    
    return res;
}

Dijkstra和Prim

Dijkstra算法用于计算有向图中的最短路径，Prim算法用于计算无向图中的最短路径。我们将他们的核心代码拿出来作比较，会发现许多共同之处。

Dijkstra:

(详情可以看我的文章：Dijkstra—求最短路径（图论，附例题、代码）_dijkstra算法求最短路径-CSDN博客)

while(1){
    int x=-1;
    for(int i=0;i<n;i++){
        if(!visit[i]&&(x<0||dist[i]<dist[x])){
            x=i;
        }
    }
            
     if(x==-1)break; 
            
    visit[x]=1;
    for(int y=0;y<n;y++){
        dist[y]=min(dist[y],dist[x]+g[x][y]);
    }
}///while

Prim:

while(1){
    int x=-1;
    for(int i=0;i<n;i++){
        if(!visited[i]&&(x==-1||dist[i]<dist[x])){
            x=i;
        }
    }

    if(x==-1)break;    ///所有节点被放入集合u，最小生成树已建立
               
    visited[x]=true;
    for(int i=0;i<n;i++){	///更新与x相邻的点的距离
        if(!visited[i])
            dist[i]=min(dist[i],g[x][i]);
    }
}

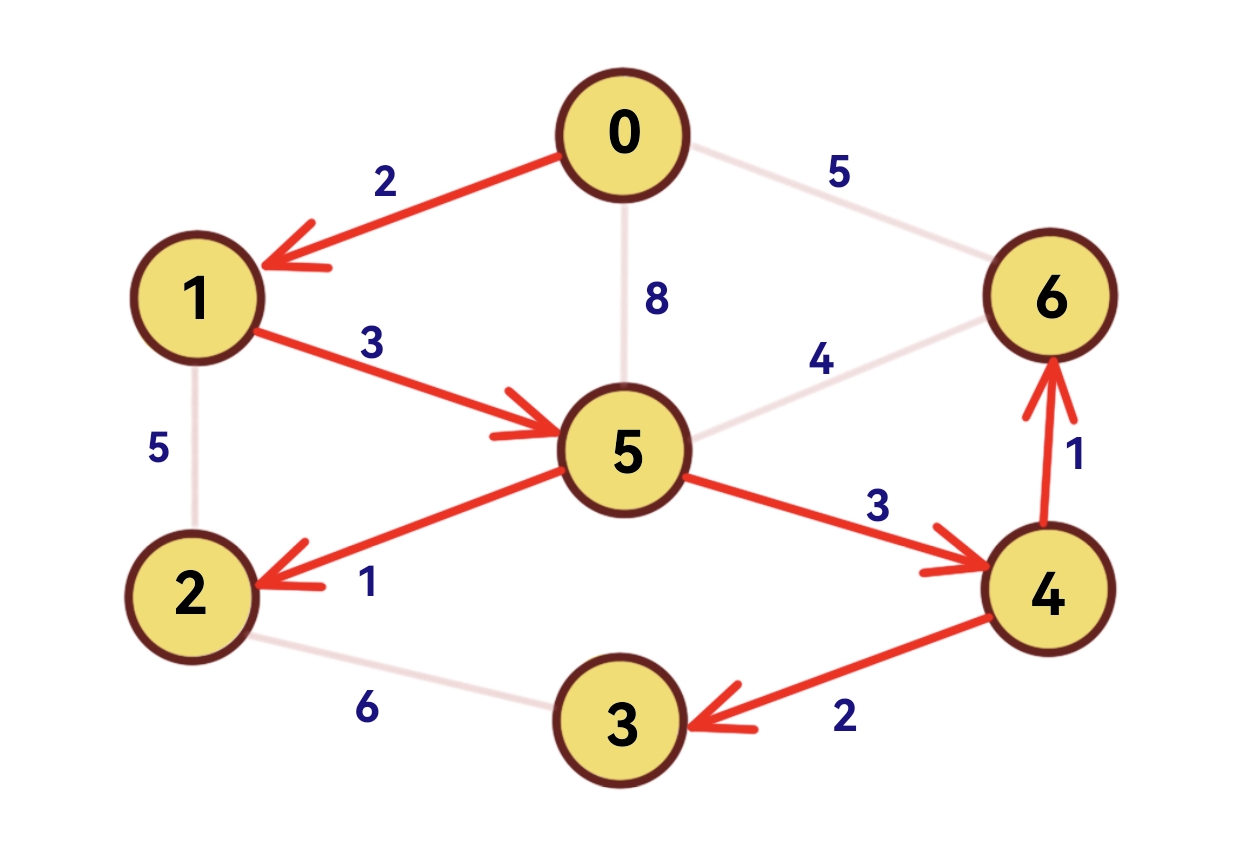
定眼一看，这俩代码不是长得一模一样吗？除了更新dist数组时，Dijkstra算法更新为dist[x]+g[x][y]，而Prim算法更新为g[x][i]。这和这两个算法的最终目的不一致有关，我们可以理解为：Dijkstra求的是不同点到源点的最短距离，在这一过程中会生成以源点为头节点的生成树，而Prim求的是，这棵树上两个节点的距离。寻找最小生成树的过程，就是寻找最短路径的过程。是不是对这两个算法又有了更深的认识？

总结

Prim算法可以直接当个模板，练熟了往上一套就可以了。