Dijkstra—求最短路径（图论，附例题、代码）

前言

在解决带权有向图的最短路径中，Dijkstra算法(迪杰斯特拉)用于解决单源有向图的最短路径问题。我们把一张有向图的起始称为源点，结束称为终点，最短路径就是从源点到终点所经历的最小权值之和。本文将介绍Dijkstra算法的原理和实用案例。

（PS.如果你是为了今天的每日一题来的，那么你找对地方了，因为本人也是特地来恶补的）

原理介绍

一、寻找最短路径

Dijkstra算法的主要思想是贪心，每次将选中距离源点最近的点，并不断更新。为实现这个目的，我们维护一个dist[]数组和一个visited[]数组，并规定：

1、图的邻接矩阵中，若a无指向b的边，将其距离视为∞(为显示直观并且防止溢出，可设为MAX=INT_MAX/2)

2、dist[i]数组表示目前更新到的i位置距离源点的最短距离。

3、visited[i]==1表示i到源点的距离已是最近，无法再更新。

我们进行以下步骤：

1、初始化邻接矩阵、dist数组和visited数组

2、扫描dist数组，找出距离源点最近的节点i（若visited[i]=1，该节点不进行比较）

3、i距离源点的最短距离已被找到，将visited[i]设为1

4、找出i指向的节点并更新他们与源点的最短距离。

5、重复2~4

请看下面这个例子：

 

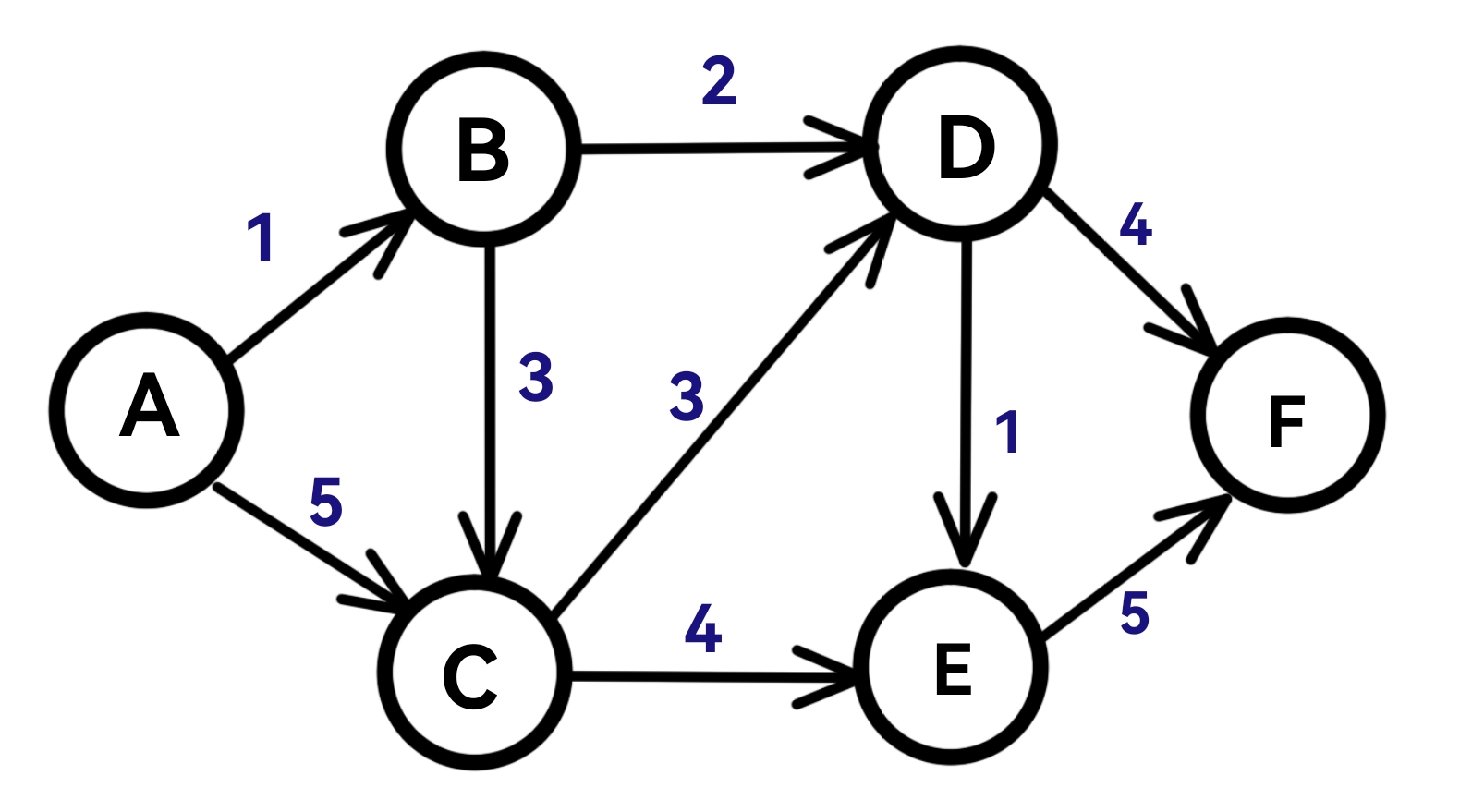
设源点为A，初始化阶段把源点dist[0]初始化为0，其余为MAX。(源点到源点的最短距离为0，其他点还未扫描到，可暂时用MAX初始化。同时，在扫描结束后，也可以依据是否有节点距离源点MAX，判断该有向图是否存在无法到达的节点。)

节点	A	B	C	D	E	F
dist	0	MAX	MAX	MAX	MAX	MAX
visited	0	0	0	0	0	0

（1）第一次扫描：

扫描dist数组，距离源点最近的节点为A，因此A到源点的最短距离为0。

将visited[ A ]设为1。

将其余点设为min (dist[ A ]+G[ A ][i] ,dist[i])

(A到源点的最短距离已经求出，更新A直接指向的点i到源点的距离，即dist[A]+G[A][i]，该点有可能比原本的dist[i]大，取最小)

节点	A	B	C	D	E	F
dist	0	1	5	MAX	MAX	MAX
visited	1	0	0	0	0	0