从幂律分布到特征数据概率分布——12个常用概率分布

在机器学习领域，概率分布对于数据的认识有着非常重要的作用。不管是有效数据还是噪声数据，如果知道了数据的分布，那么在数据建模过程中会得到很大的启示。

首先，如下图所示8个特征数据概率分布情况（已经做归一化），这些特征是正态分布、伯努利分布，还是泊松分布、幂律分布？

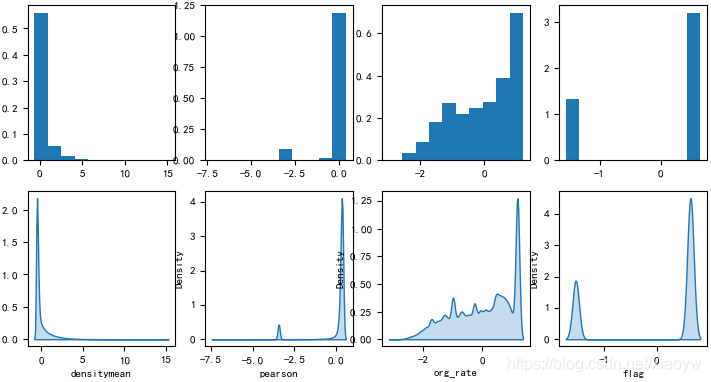
在高斯法则生效的领域，平均值可以代表整体。但是在幂律法则统治的领域，平均值毫无意义。高斯法则和幂律法则的典型代表是分别身高和财富，把姚明放到100个人中，并不会显著改变平均身高，但把比尔·盖茨放到100个人中，就会极大改变平均财富。

在高斯法则生效的领域，所有人跟平均值的差距不会很大；但是在幂律法则分布的领域，跟平均值的差距就会大到惊人。

正态法则和幂律法则，细思极恐。带着问题，我们开始概率分布之旅。

1. 概率分布概述

概率分布，是指用于表述随机变量取值的概率规律。将随机变量作为横轴，概率作为纵轴，把随机变量与对应变量画上去，构成一个图形，这个图像就是概率分布的直观表示。通常也用概率分布函数表示$F(x)$来描述一个概率分布，概率分布函数被定义为：
F ( x ) = P { X < x } F ( x ) =P\{X<x\} F(x)=P{X<x}

总之概率分布也可以理解为一个函数，它刻画了随机变量与概率的映射关系，给定一个概率分布，就可以求任何随机变量对应的概率了。当一个随机变量与它的概率满足某一个概率分布的映射关系时，则称这个随机变量服从该概率分布。

如下图为常用概率分别关系图。

2. 常用概率分布

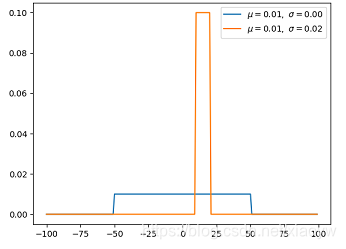
2.1. 均匀分布

均匀分布在 [a，b] 上具有相同的概率值，是简单概率分布。
均匀分布可以很容易地从伯努利分布中得出。在这种情况下，结果的数量可能不受限制，并且所有事件的发生概率均相同。例如掷骰子，存在多个可能的事件，每个事件都有相同的发生概率。

2.2. 伯努利分布

伯努利分布（Bernoulli Distribution）是单个二值随机变量的分布，是一种离散分布，又称为 “0-1 分布” 或 “两点分布”。例如抛硬币的正面或反面，物品有缺陷或没缺陷，病人康复或未康复，此类满足「只有两种可能，试验结果相互独立且对立」的随机变量通常称为伯努利随机变量。

假设二值其中之一的概率等于$p$，而对于互斥对立面面则是$（1-p）$（包含所有可能结果的互斥事件的概率总和为1）。

对于伯努利分布来说，其离散型随机变量期望为：
$E(x)=\sum x\times p(x)=1\times p+0\times (1-p)=p$
$E(x^2)=\sum x\times p(x^2)=1^2\times p+0^2\times (1-p)=p$

方差为：
$Var(x)=E(x^2)-(E(x){)}^2=p-p^2=p(1-p)$

2.3. 二项分布

二项分布（binomial distrubution）就是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。

P { X = k } = ( n k ) p k ( 1 − p ) ( n − k ) P\{X=k\}=\binom{n}{k}p^k(1-p)^{(n-k)} P{X=k}=(kn​)pk(1−p)(n−k)

式中$k=0,1,2,...,n$，$\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\frac{n!}{k!(n-k)!}$是二项式系数，又记为$C_n^k$。

二项式分布的主要特征是：

给定多个试验，每个试验彼此独立（一项试验的结果不会影响另一项试验）。

每个试验只能得出两个可能的结果（例如，获胜或失败），其概率分别为p和（1- p）。

如果获得成功概率（p）和试验次数（n），则可以使用以下公式计算这n次试验中的成功概率（x）。

如果二项分布满足p<q，np≥5，(或p>q，np≥5)时，二项分布接近正态分布。

$E(X)=np$
$Var(X)=np(1-p)$

2.4. 多项分布

多项式分布（Multinoulli distribution）二项分布的推广。二项分布（也叫伯努利分布）的典型例子是扔硬币，硬币正面朝上概率为p, 重复扔n次硬币，k次为正面的概率即为一个二项分布概率。而多项分布就像扔骰子，有6个面对应6个不同的点数。

某随机实验如果有k个可能结局$A_1、A_2、\dots 、A_k$，分别将他们的出现次数记为随机变量$X_1、X_2、\dots 、X_k$，它们的概率分布分别是$p_1，p_2，\dots ，p_k$，那么在n次采样的总结果中，$A_1$出现$n_1$次、$A_2$出现$n_2$次、…、$A_k$出现$n_k$次的这种事件的出现概率P有下面公式：

$$P(X_1=n_1,X_2=n_2,\cdots ,X_k=n_k)=\{\begin{array}{cc}\frac{n!}{n1!n2!\cdots nk!}{p}_1^{n1}{p}_2^{n2}\cdots p_k^{nk}& ,{\sum }_{i=1}^k{n}_i=n\\ 0& ,ortherwise\end{array}$$

多项分布对其每一个结果都有均值和方差，分别为：

$E(X_i)=n{p}_i$
$Var(X_i)=n{p}_i(1-p_i)$

2.5. 泊松分布

泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数，电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、激光的光子数分布等等。【维基百科】

$P(X=k)=\frac{{\lambda }^k}{k!}{e}^{-\lambda },k=0,1,...$

泊松分布的参数$\lambda$是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为$\lambda$

一般来说，我们会换一个符号，让 $\mu =\lambda$ 。

2.6. 正态分布

若随机变量$X$服从一个数学期望为$\mu$、方差为${\sigma }^2$的正态分布，记为$N(\mu ，{\sigma }^2)$。其概率密度函数为正态分布的期望值$\mu$决定了其位置，其标准差$\sigma$决定了分布的幅度。当$\mu =0,\sigma =1$时的正态分布是标准正态分布。

标准正态分布又称为$u$分布，是以0为均数、以1为标准差的正态分布，记为$N（0，1）$。

一维正态分布
若随机变量$X$服从一个位置参数为$\mu$ 、尺度参数为$\sigma$的概率分布，且其概率密度函数为：
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{(-\frac{(x-\mu {)}^2}{2{\sigma }^2})}$$

标准正态分布
当$\mu =0，\sigma =1$时，正态分布就成为标准正态分布：
$$f(x)=\frac{1}{\sqrt{2\pi }}{e}^{(-\frac{x^2}{2})}$$

2.7. 伽马分布

伽玛分布（Gamma Distribution），Gamma分布中的参数α，称为形状参数（shape parameter），β称为尺度参数（scale parameter）。
“指数分布”和“${\chi }^2$分布”都是伽马分布的特例。

令$X\sim \Gamma (\alpha ,\beta )$；且令$\lambda =\frac{1}{\beta }$： （即$X\sim \Gamma (\alpha ,\frac{1}{\lambda })）$。

$f(X)=\frac{X^{(\alpha -1)}{\lambda }^{\alpha }{e}^{(-\lambda X)}}{\Gamma (\alpha )}，X>0$

2.8. 几何分布

几何分布（Geometric distribution）在伯努利试验中，记每次试验中事件$A$发生的概率为$p$，试验进行到事件A出现时停止，此时所进行的试验次数为$X$，其分布列为：

$$P(X=k)=(1-p{)}^{(k-1)}p,k=1,2,...$$
此分布列是几何数列的一般项，因此称$X$服从几何分布，记为$X～GE(p)$ 。
实际中有不少随机变量服从几何分布，譬如，某产品的不合格率为0.05，则首次查到不合格品的检查次数$X～GE(0.05)$ 。

$X\sim GE(p)，q=1-p，P(X=r)=p{q}^{(r-1)}$，当$r\to \infty$时：

期望和方差：

$E(X)=\frac{1}{p}$
$Var(X)=\frac{q}{p^2}$

2.9. 指数分布

在概率理论和统计学中，指数分布（Exponential distribution也称为负指数分布）是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程。 这是伽马分布的一个特殊情况。 它是几何分布的连续模拟，它具有无记忆的关键性质。 除了用于分析泊松过程外，还可以在其他各种环境中找到。

$$f(x)=\{\begin{array}{cc}\lambda e^{-(\lambda x)}& ,x>0\\ 0& ,x\le 0\end{array}$$

在概率论和统计学中，指数分布是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等。

许多电子产品的寿命分布一般服从指数分布。有的系统的寿命分布也可用指数分布来近似。它在可靠性研究中是最常用的一种分布形式。指数分布是伽玛分布和威布尔分布的特殊情况，产品的失效是偶然失效时，其寿命服从指数分布。

期望与方差：
$E(X)=\frac{1}{\lambda }$
$Var(X)=\frac{1}{{\lambda }^2}$

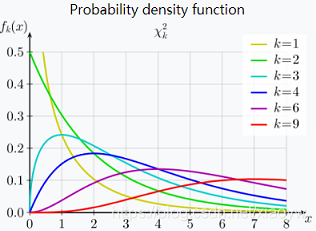
2.10. 卡方分布

卡方分布（chi-square distribution），也称为$X^2$分布，若$n$个相互独立的随机变量${\xi }_1,{\xi }_2，...,{\xi }_n$，均服从标准正态分布（也称独立同分布于标准正态分布），则这$n$个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为卡方分布。

${\chi }^2(n)$ 分 布 , 就 是 $\Gamma$ 分 布 的 一 种 特 殊 形 式：

其中$\alpha =\frac{n}{2},\beta =\frac{1}{2}$

$$f(x)=\{\begin{array}{cc}\frac{1}{2^{\frac{n}{2}}\Gamma (\frac{n}{2})}{x}^{\frac{n}{2}-1}{e}^{-\frac{1}{2}x}& ,x>0\\ 0& ,x\le 0\end{array}$$

定义 如果随机变脸$X_i$ 之 间 相 互 独 立 且 服 从 $N(0,1)$ , 分 布 , 则 称 随 机 变 量
${\chi }^2=X_1^2+X_2^2+...+X_n^2$ 服从自由度为$n$ 的 ${\chi }^2$ 分 布 记 为${\chi }^2\sim X^2(n)$

2.11. beta分布

贝塔分布（Beta Distribution) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数，在机器学习和数理统计学中有重要应用。在概率论中，贝塔分布，也称$B$分布，是指一组定义在(0,1) 区间的连续概率分布。
$$f(x:\alpha ,\beta )=\frac{1}{B(\alpha ,\beta )}{x}^{(\alpha -1)}(1-x{)}^{(\beta -1)}$$
其中$\Gamma (z)$ 是$\Gamma$函数。随机变量$X$服从参数为$(\alpha ,\beta )$ 的$B$分布通常写作
$$X\sim BeB(\alpha ,\beta )$$

2.12. 幂律分布

幂律分布是指某个具有分布性质的变量，且其分布密度函数是幂函数（由于分布密度函数必然满足“归一律”，所以这里的幂函数，一般规定小于负1）的分布。

幂律分布表现为一条斜率为幂指数的负数的直线,这一线性关系是判断给定的实例中随机变量是否满足幂律的依据。

假设变量x服从参数为 的幂律分布，则其概率密度函数可以表示为：
$$f(x)=c{x}^{-\alpha -1},x\to \infty$$

在双对数坐标下，幂律分布表现为一条斜率为幂指数的负数的直线，这一线性关系是判断给定的实例中随机变量是否满足幂律的依据。

Zipf定律与Pareto定律（帕累托定律）
对“长尾”分布研究做出重要贡献的是Zipf和Pareto ，虽然他们并不是这种分布的最早发现者。Zipf定律与Pareto定律都是简单的幂函数，我们称之为幂律分布。

3. 总结

回顾本文的开始，幂律分布的长尾现象很普遍，大数据中小概率数据普遍存在，如何解决呢？

我的方法是把数据$\sqrt[3]{x}$，对模型的精度结果影响只有不到千分之一，也就是说数据变换缩短尾巴效果有限。另外的方法，是从整体模型上考虑细分，二八原则中，把20%的分离出来，自顶向下逐步精确。

参考：

【1】视学算法，数据分析必须掌握的概率分布！建议收藏！ CSDN博客 ，2019.11
【2】数据派THU，深度学习必懂的 13 种概率分布（附链接） CSDN博客，2020.02
【3】马同学图解数学, 如何通俗理解泊松分布？ CSDN博客，2019.04
【4】刘之帅，机器学习中的“分布” CSDN博客，2020.04
【5】我是8位的，概率统计14——几何分布 博客园 ，2020.01
【6】sam-X，正态和伽马分布族 CSDN博客，2018.09
【7】娜娜酱，生存法则—正态分布和幂律分布 知乎，2018.07