Multiclass Classification With Sklearn

https://towardsdatascience.com/comprehensive-guide-to-multiclass-classification-with-sklearn-127cc500f362

Precision, Recall and F1 scores for multiclass classification

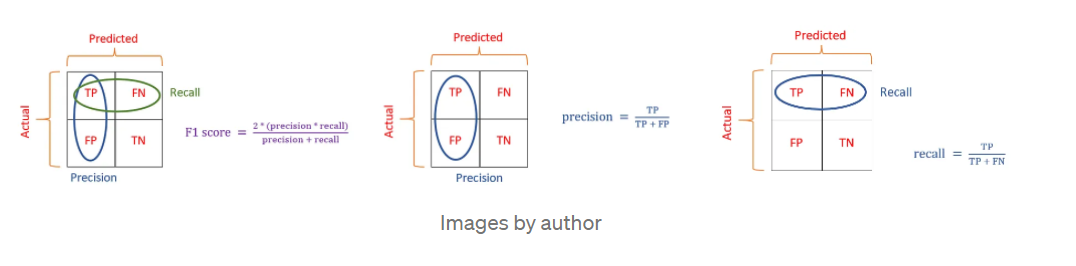
A better metric to measure our pipeline’s performance would be using precision, recall, and F1 scores. For the binary case, they are easy and intuitive to understand:

In a multiclass case, these 3 metrics are calculated per-class basis. For example, let’s look at the confusion matrix again:

# Plot the confusion matrix
fig, ax = plt.subplots(figsize=(12, 8))
# Create the matrix
cm = confusion_matrix(y_test, y_pred)
cmp = ConfusionMatrixDisplay(cm, display_labels=pipeline.classes_)
cmp.plot(ax=ax)

plt.show();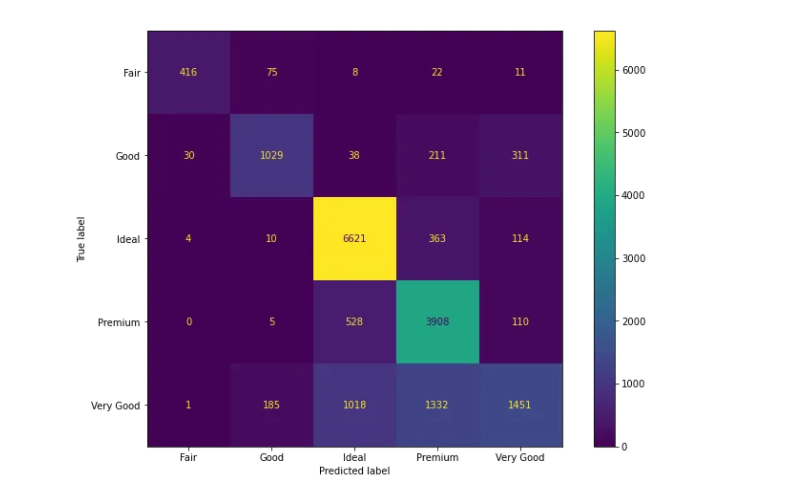

Precision tells us what proportion of predicted positives is truly positive. If we want to calculate precision for Ideal diamonds, true positives would be the number of Ideal diamonds predicted correctly (the center of the matrix, 6626). False positives would be any cells that count the number of times our classifier predicted other types of diamonds as Ideal. These would be the cells above and below the center of the matrix (1013 + 521 + 31 + 8 = 1573). Using the formula of precision, we calculate it to be:

Precision (Ideal) = TP / (TP + FP) = 6626 / (6626 + 1573) = 0.808

Recall is calculated similarly. We know the number of true positives — 6626. False negatives would be any cells that count the number of times the classifier predicted the Ideal type of diamonds belonging to any other negative class. These would be the cells right and left to the center of the matrix (3 + 9 + 363 + 111 = 486). Using the formula of recall, we calculate it to be:

Recall (Ideal) = TP / (TP + FN) = 6626 / (6626 + 486) = 0.93

So, how do we choose between recall and precision for the Ideal class? It depends on the type of problem you are trying to solve. If you want to minimize the instances where other, cheaper types of diamonds are predicted as Ideal, you should optimize precision. As a jewelry store owner, you might be sued for fraud for selling cheaper diamonds as expensive Ideal diamonds.

On the other hand, if you want to minimize the instances where you accidentally sell Ideal diamonds for a lower price, you should optimize for recall of the Ideal class. Indeed, you won’t get sued, but you might lose money.

The third option is to have a model that is equally good at the above 2 scenarios. In other words, a model with high precision and recall. Fortunately, there is a metric that measures just that: the F1 score. F1 score takes the harmonic mean of precision and recall and produces a value between 0 and 1:

So, the F1 score for the Ideal class would be:

F1 (Ideal) = 2 * (0.808 * 0.93) / (0.808 + 0.93) = 0.87

Up to this point, we calculated the 3 metrics only for the Ideal class. But in multiclass classification, Sklearn computes them for all classes. You can use classification_report to see this:

from sklearn.metrics import classification_report

>>> print(classification_report(y_test, y_pred))

               precision    recall  f1-score   support

        Fair       0.92      0.78      0.85       532
        Good       0.79      0.64      0.70      1619
       Ideal       0.81      0.93      0.86      7112
     Premium       0.67      0.86      0.75      4551
   Very Good       0.73      0.36      0.48      3987

    accuracy                           0.75     17801
   macro avg       0.78      0.71      0.73     17801
weighted avg       0.76      0.75      0.74     17801

You can check that our calculations for the Ideal class were correct. The last column of the table — support shows how many samples are there for each class. Also, the last 2 rows show averaged scores for the 3 metrics. We already covered what macro and weighted averages are in the example of ROC AUC.

For imbalanced classification tasks such as these, you rarely choose averaged precision, recall of F1 scores. Again, choosing one metric to optimize for a particular class depends on your business problem. For our case, we will choose to optimize the F1 score of Ideal and Premium classes (yes, you can choose multiple classes simultaneously). First, let’s see how to calculate weighted F1 across all class:

from sklearn.metrics import f1_score

# Weighed F1 across all classes
>>> f1_score(y_test, y_pred, average="weighted")
0.7355520553610462

The above is consistent with the output of classification_report. To choose the F1 scores for Ideal and Premium classes, specify the labels parameter:

# F1 score for Ideal and Premium with weighted average
>>> f1_score(
...    y_test, y_pred, labels=["Premium", "Ideal"], average="weighted"
...  )
0.8205313467958754