阿贝尔定理:
如果幂级数  在 点 x = x₀(x₀≠0)处收敛, 则对于适合不等式 |x| < |x₀|的一切x, 都有幂级数
在 点 x = x₀(x₀≠0)处收敛, 则对于适合不等式 |x| < |x₀|的一切x, 都有幂级数 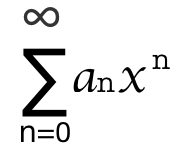 在点 x 处绝对收敛;
在点 x 处绝对收敛;
反之,如果幂级数  在点 x = x₀ (x₀≠0)处发散, 则对于适合不等式 |x| > |x₀|的一切 x, 都有幂级数
在点 x = x₀ (x₀≠0)处发散, 则对于适合不等式 |x| > |x₀|的一切 x, 都有幂级数  在点 x发散。
在点 x发散。
~~~~~~~~~~~~~~~~~~~~
这个定理告诉我们, 若存在x₀ ≠ 0, 使得幂级数  在点x₀ 处收敛, 则原幂级数在开区间(-|x₀|, |x₀|)内处处绝对收敛;
在点x₀ 处收敛, 则原幂级数在开区间(-|x₀|, |x₀|)内处处绝对收敛;
若存在x₁, 使得原幂级数在点x₁处发散, 则原幂级数 在(- ∞, -|x₁|) ∪ (|x₁|, +∞)内处处发散。
~~~~~~~~~~~~
容易看出,对于这样的幂级数, 必然存在一个正数 R>0, 使得对于满足|x| < R的一切x, 都有该幂级数绝对收敛, 从而该幂级数收敛; 对于满足 |x| >R的一切x, 都有该幂级数发散; 对于 x = ±R这两点, 幂级数的敛散性不能确定, 需要具体分析。
有以下定义: 定义R为原幂级数的收敛半径, 称开区间(-R, R) 为该幂级数的收敛区间。
可以看到,区间的定义就是一个开区间。








 本文介绍了阿贝尔定理,阐述了幂级数在收敛点周围绝对收敛的性质,包括收敛半径的定义和发散情况的判断准则。重点在于理解收敛区间与收敛半径的概念及其应用。
本文介绍了阿贝尔定理,阐述了幂级数在收敛点周围绝对收敛的性质,包括收敛半径的定义和发散情况的判断准则。重点在于理解收敛区间与收敛半径的概念及其应用。

















 294
294

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








