概论_第7章_参数估计__区间估计

先看知识结构图

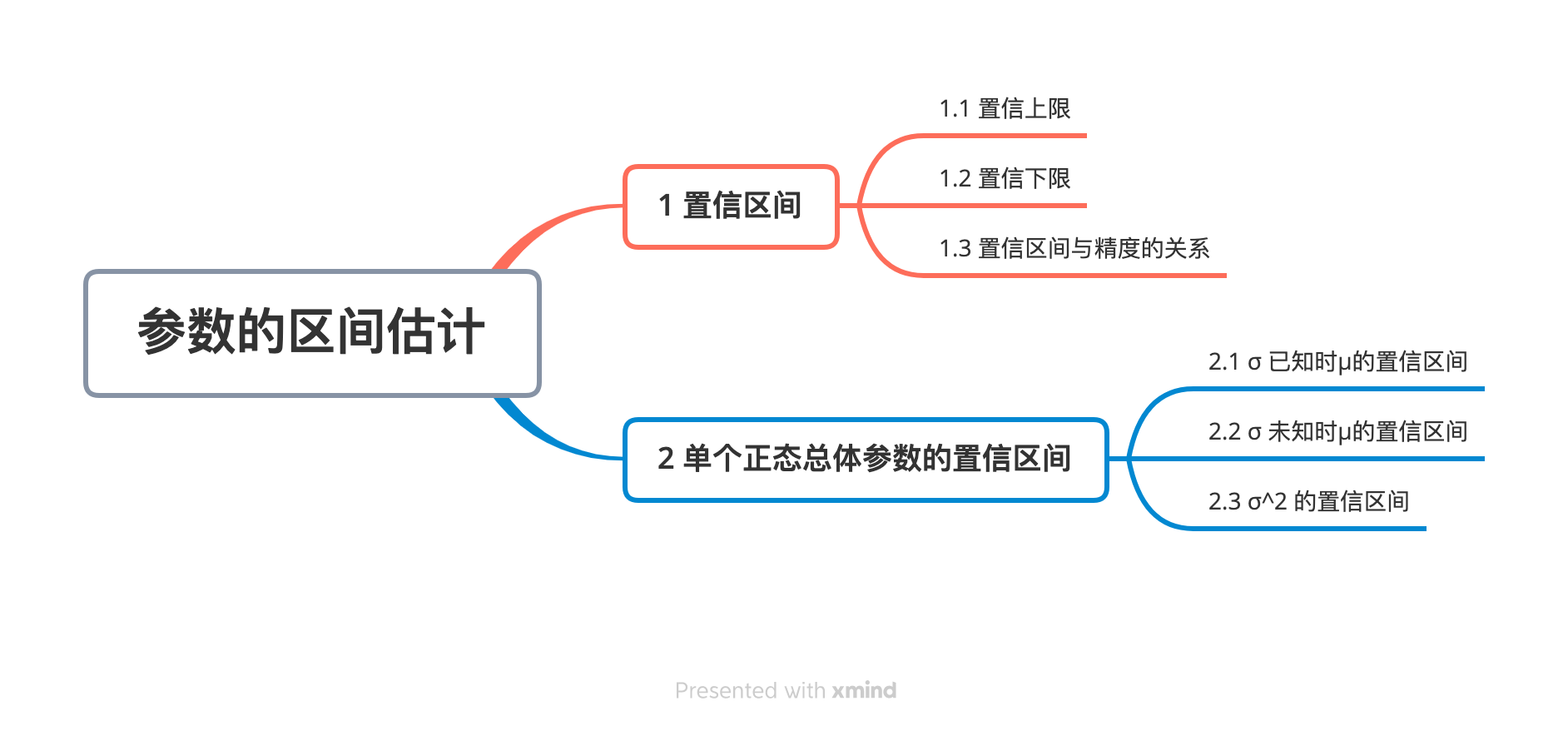
区间估计，分为 期望的区间估计、 方差的区间估计。
首先讲置信区间， 置信区间在考试时出大题的概率90%。

一 置信区间 定义

定义： 设$\sigma$ 为总体的未知参数， ${\hat{\theta }}_1={\hat{\theta }}_1(x_1,x_2,...,x_n),{\hat{\theta }}_2={\hat{\theta }}_2(x_1,x_2,...,x_n)$是由样本 $x_1,x_2,...,x_n$定出的两个统计量， 若对于给定的概率 1 — $\alpha$ ( 0< $\alpha$ < 1), 有

$P${${\hat{\theta }}_1\le \theta \le {\hat{\theta }}_2$}$=1-\alpha$

则随机区间[${\hat{\theta }}_1$ , ${\hat{\theta }}_2$]称为参数 $\theta$ 的置信度为 $1-\alpha$ 的置信区间, ${\hat{\theta }}_1$ 称为置信下限，
${\hat{\theta }}_2$ 称为置信上限。

注意这里: 1- $\alpha$ 称为置信度， $[{\hat{\theta }}_1,{\hat{\theta }}_2]$ 称为置信区间。

置信区间的意义可作如下解释： $\theta$ 包含在随机区间 $[{\hat{\theta }}_1,{\hat{\theta }}_2]$ 中的概率为 1 — $\alpha$。 粗略地说， 若$\alpha$ 等于0.05， 在100次抽样中， 大致有95次 $\theta$ 包含在$[{\hat{\theta }}_1,{\hat{\theta }}_2]$中， 而其余 5 次可能不在该区间。

$\alpha$ 常取的数值为 $0.05$， $0.01$, 此时1— $\alpha$ 分别为$0.95$ , $0.99$.

注意这样说法：
参数为 ** 的置信度为 ** 的置信区间。

对这种说法，我们要适应，不要管拗口， 我们要学会， 要掌握。

~~~~~~~~
置信区间的长度可视为区间估计的精度。下面分析置信度与精度的关系。
（1）当置信度 $1-\alpha$ 增大， 又样本容量 n 固定时， 置信区间长度增大， 即区间估计精度减低；
当置信度 $1-\alpha$ 减小， 又样本容量n固定， 置信区间长度减小， 即区间估计精度提高。

（2） 设置信度 $1-\alpha$ 固定， 当样本容量n增大时， 置信区间长度减小， 区间估计精度提高。
~~~~~~~~

二 单个正态总体参数的置信区间

2.1 $\sigma$ 已知时 $\mu$ 的置信区间
设总体X~N($\mu ,{\sigma }^2$), ${\sigma }^2$ 已知， $\mu$ 未知， $\mu$ 的置信度为 $1-\alpha$ 的置信区间为

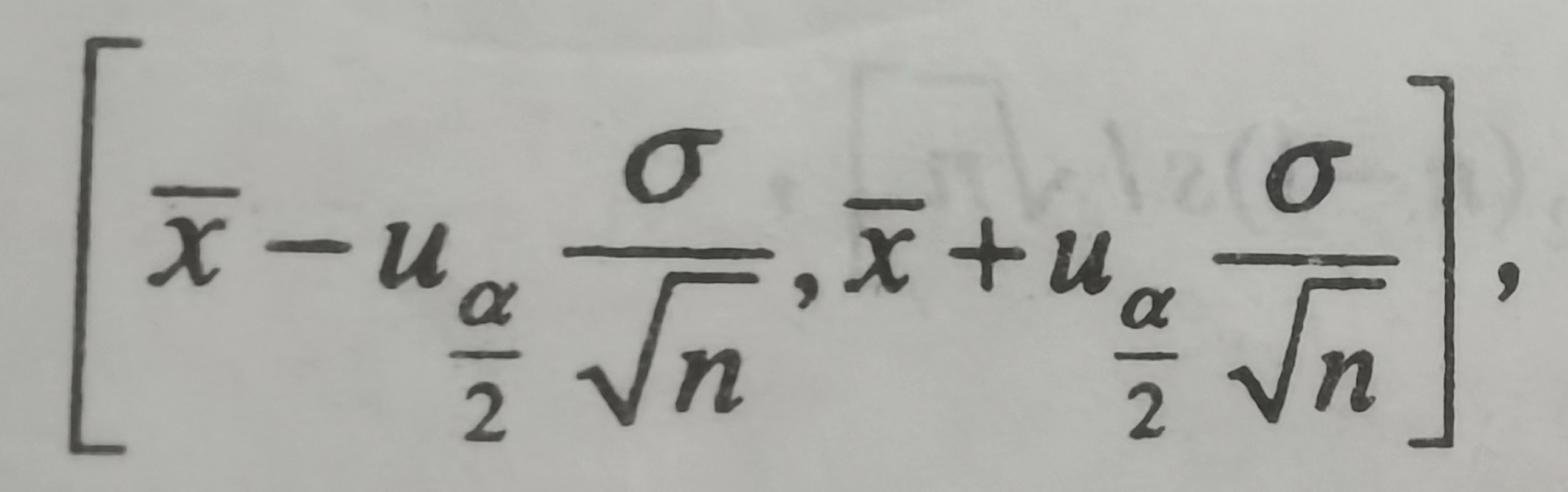
注： $u$ 表示统计量，通常写法为$u$${}_{\frac{\alpha }{2}}$

2.2 $\sigma$未知时 $\mu$ 的置信区间
此时， t 统计量的自由度为n -1

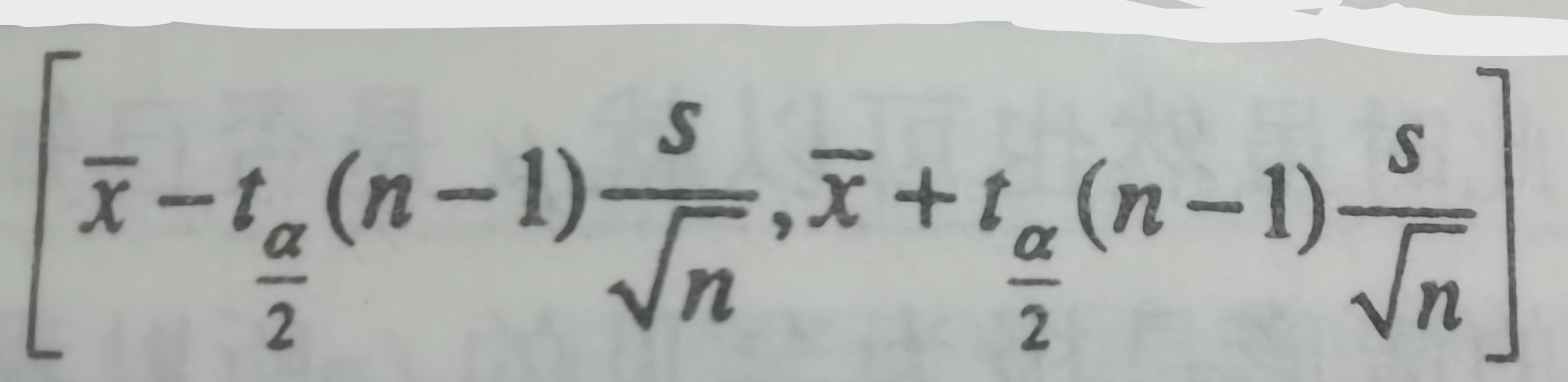
2.3 $\sigma$${}^2$ 的置信区间， 我们只讨论 $\mu$ 未知时 $\sigma$${}^2$的置信区间。
虽然也可以分两种情况。
此时， 卡方统计量 自由度为 n-1.

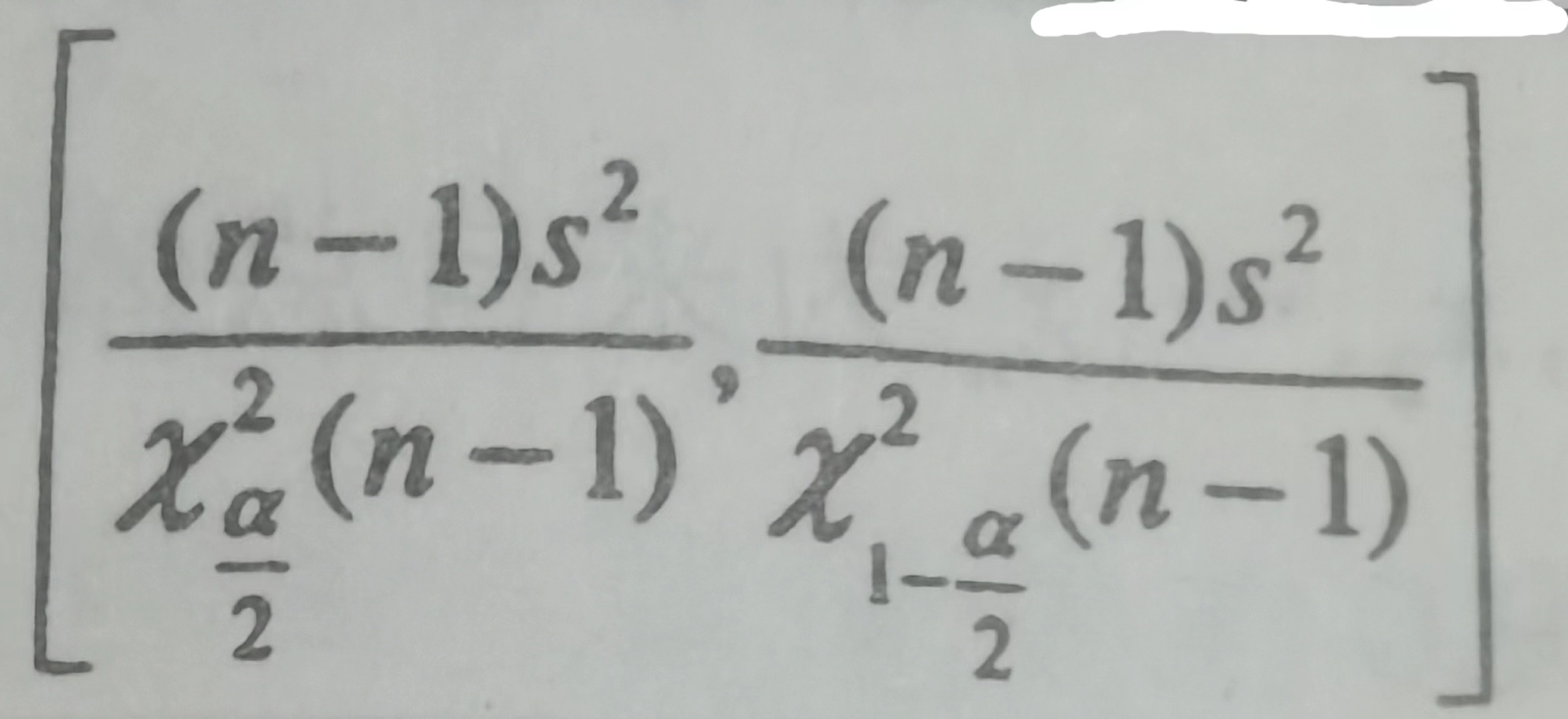
三 光说不练假把式， 看例题

例1 2008.7

来自正态总体 $X$ ~ $N(\mu ,0.81)$, 容量n=9 的简单随机样本， 样本均值为5， 则未知参数 $\mu$ 的置信度为0.95的置信区间是__________($u_{0.025}=1.96$, $u_{0.05}=1.645$)
解： 本题 适用于 2.1 的情形。
统计量 $u=\frac{\overline{x}-\mu }{\sigma /\sqrt{n}}$ 置信区间, 套用公式:
[ $\overline{x}-u_{\frac{\alpha }{2}}\frac{\sigma }{\sqrt{n}}$ , $\overline{x}+u_{\frac{\alpha }{2}}\frac{\sigma }{\sqrt{n}}$ ]，
由题意已知， $\overline{x}=5$, $\sigma =0.9$, ${\mu }_{\frac{\alpha }{2}}=1.96$,
所以 置信区间为 5 $\mp$ 1.96 * 0.9/3。
~~~~~

例2 2010.10

设某行业的一项经济指标服从正态分布 $N(\mu ,{\sigma }^2)$, 其中$\mu ,{\sigma }^2$ 均未知， 今获取了该指标的 9 个数据作为样本， 并算得样本均值 $\overline{x}=56.93$, 样本方差$s^2=(0.93{)}^2$, 求 $\mu$ 的置信度为0.95的置信区间。 （附 $t_{0.025}(8)=2.306$）
解： 本题 ${\sigma }^2$ 未知， 跟上例 不同了。
  本题 适用于2.2 的情形。
统计量 $t=\frac{\overline{x}-\mu }{s/\sqrt{n}}$, t 的自由度为n-1.
套用公式：
[ $\overline{x}-t_{\frac{\alpha }{2}}(n-1)\frac{s}{\sqrt{n}}$ , $\overline{x}+t_{\frac{\alpha }{2}}(n-1)\frac{s}{\sqrt{n}}$]

所以置信区间为 56.93 $\mp$ 2.306*0.93/3

要记住： 只要$\sigma$未知， 要得出$\mu$只能用 t 统计量。此时要注意自由度为 n-1.

例3 2007.10 大题， 本题10分

车床加工零件长度 X 服从正态分布 N($\mu ,{\sigma }^2$), 现随机抽取 4 个， 测得样本方差 $s^2$ = 7.5, 求总体方差${\sigma }^2$ 的置信度为 0.95的置信区间。(附: ${\chi }_{0.025}^2(3)=9.348,{\chi }_{0.975}^2(3)=0.216,{\chi }_{0.025}^2(4)=11.143,{\chi }_{0.975}^2(4)=0.484$)

解： 本题 未知$\mu$ , 求${\sigma }^2$, 适用于2.3 的情形。
即 ${\chi }^2$分布的置信区间。
${\chi }^2$的自由度为： n-1， 套用公式：
[ $\frac{(n-1)s^2}{{\chi }_{\frac{\alpha }{2}}^2(n-1)}$ , $\frac{(n-1)s^2}{{\chi }_{1-\frac{\alpha }{2}}^2(n-1)}$ ]

n-1 = 3, 所以附 提供的值，有(4)的都是干扰值。
注意 ${\chi }_{\frac{\alpha }{2}}^2(3)=9.348,{\chi }_{1-\frac{\alpha }{2}}^2(3)=0.216$

所以置信区间=[ 3 * 7.5/9.348, 3*7.5/0.216] = [2.407, 104.17]。

我们要仔细牢记以上3个例题的 公式。

此表，我们必须牢记， 必须掌握！！！